ИНФОРМАЦИОННЫЕ МОДЕЛИ

ПРИ РАЗРАБОТКЕ ТРЕНАЖЕРОВ ТРАНСПОРТНЫХ СИСТЕМ

¹Будылина Е.А., ²Гарькина И.А., ²Данилов А.М.

¹Московский государственный машиностроительный университет

²Пензенский государственный университет архитектуры и строительства

Идентификация целостной эргатической системы по сравнению с простой технической осложняется присутствием в ней человека, деятельность которого плохо формализуется (особенно сравнение концептуальной модели движения с информационной). Наиболее актуальны ответы на вопросы [1,2]:

- что понимать под управляющими воздействиями человека-оператора,

- как практически определить параметры оптимального управления,

- как установить связь параметров управления с техническими характеристиками объекта,

- как определить передаточные функции объекта и оператора по данным нормального функционирования эргатической системы,

- как определить имитационные характеристики тренажера из условия формирования требуемого стиля управления,

- как оценить необходимую точность идентификации двух систем: «оператор – имитатор», «оператор – реальный объект», исходя из недопустимости формирования у обучаемых ложных навыков и др.

Задача определения управляющих воздействий оператора (стабилизация программного движения без флуктуаций в его поведении) может быть решена в основном лишь с использованием некоторой итерационной процедуры. Это относится и к определению передаточных функций объекта и оператора по данным нормальной эксплуатации. Как видим, прямая идентификация эргатической системы в силу ее замкнутости через человека встречает, по существу, непреодолимые трудности.

Определение управляющих воздействий оператора (стабилизация программного движения без флуктуаций в его поведении) возможно лишь с использованием некоторой итерационной процедуры. Это относится и к определению передаточных функций объекта и оператора по данным нормальной эксплуатации. Непосредственная идентификация эргатической системы в силу ее замкнутости через человека встречает, по существу, непреодолимые трудности.

Классическим, традиционным считается определение оценки передаточных функций по спектральным характеристикам. Однако наблюдается сильное расхождение результатов в зависимости от параметров дискретизации, длительности рассматриваемых реализаций и применяемых для сглаживания различных типов «окон» (с неизбежными элементами субъективизма при их выборе).

Известно, что точность определения передаточных характеристик вдали от доминирующих частот крайне низка. Правда, в этих зонах высокая точность и не нужна: оператор управляет объектом на частотах, близких к его собственной частоте (связь входного сигнала со спектральной характеристикой, рис.1).

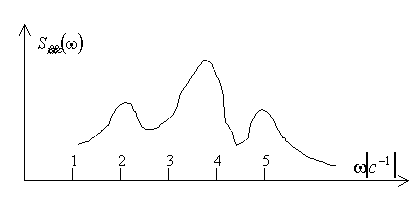
Рис.1. Энергетический спектр

Для некоторых режимов функционирования зоны доминирующих частот (здесь возможна их линейная аппроксимация) можно определить по обобщенным АЧХ и ФЧХ (решением уравнений идентификации). В этих зонах оператор воспринимает объект как усилительное звено с запаздыванием.

Идентификация динамической системы в частотной области относится к классу некорректных задач. Так, для разомкнутой стационарной системы с одним входом и одним выходом импульсная переходная функция определяется выражением

,

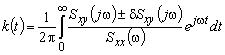а норма ошибки решения -

.

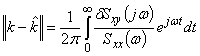Как видим, ошибка может быть как угодно велика в зависимости от распределения спектральной плотности входного сигнала (если и имеют нули одинаковой кратности в какой-либо конечной точке оси , то погрешность решения может быть как угодно большой). Для рассматриваемого здесь класса эргатических систем рабочая частотная область по каждому из каналов управления достаточно узка (0,7…7 с^-1). Точность определения частотных передаточных функций зависит от спектральной плотности входного сигнала. Обычно оценка точности определения на разных частотах производится с весом, пропорциональным спектральной плотности , в соответствии с -критерием:

.

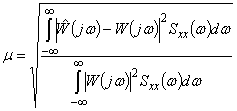Вблизи каждой характерной («резонансной») частоты входного сигнала возможна линейная аппроксимация частотных характеристик (рис.2; согласуется с полученными по данным нормальной эксплуатации обобщенными частотными характеристиками; 5 с^-1 – резонансная частота по одному из каналов).

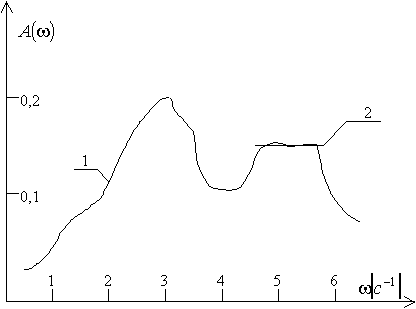
Рис.2. Обобщенные частотные характеристики:

кривая 1 – экспериментальная, 2 – аппроксимированная

Наибольшими возможностями обладают регрессионные методы идентификации; легко обобщаются на случай инерционного оператора с чистым запаздыванием (при переменных коэффициентах в уравнениях движения - аппроксимация с использованием полиномов Ньютона, методом наименьших произведений или квадратов).

Приведенный подход широко использовался на практике при разработке тренажеров транспортных систем.

Литература

1. Данилов А.М., Домке Э.Р., Гарькина И.А. Формализация оценки оператором характеристик объекта управления / Информационные системы и технологии, №2 (70), 2012. С.5-11.

2. Данилов А.М. Математическое моделирование управляющих воздействий оператора в эргатической системе / А.М.Данилов, Э.Р.Домке, И.А.Гарькина // Вестник МАДИ, №2, 2011. – С.18-23.