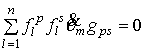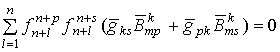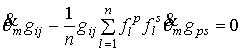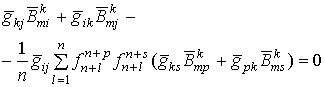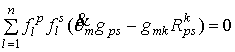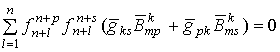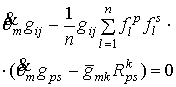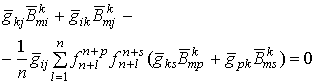Математика/4.Прикладная математика
К. ф.-м. н. Якунина О.В.
Пензенский государственный университет
ПРИЗНАКИ КЛАССОВ НАВЕЙРА
СПЕЦИАЛЬНОЙ РИМАНОВОЙ СТРУКТУРЫ ПОЧТИ ПРОИЗВЕДЕНИЯ
На касательном расслоении гладкого многообразия рассматривается риманова структура почти произведения, горизонтальное распределение которой определяется заданной инфинитезимальной связностью. Для данной структуры получены признаки классов Навейра.
1. Пусть ![]() - гладкое n-мерное многообразие, g - риманова метрика на
- гладкое n-мерное многообразие, g - риманова метрика на ![]() . Римановой структурой почти произведения на
. Римановой структурой почти произведения на ![]() называется тензорное
поле P типа (1,1), удовлетворяющее условиям:
называется тензорное
поле P типа (1,1), удовлетворяющее условиям:
![]() , (1)
, (1)
![]() (2)
(2)
для любых векторных полей X,Y на ![]()
В каждой точке ![]() можно рассмотреть два
подпространства
можно рассмотреть два
подпространства ![]() : горизонтальное
: горизонтальное ![]() , все векторы которого отвечают собственному значению
оператора
, все векторы которого отвечают собственному значению
оператора ![]() , равному -1, и вертикальное
, равному -1, и вертикальное ![]() , соответствующее собственному значению +1. Таким образом, на
, соответствующее собственному значению +1. Таким образом, на
![]() определены 2
дополнительных взаимно ортогональных распределения – горизонтальное
определены 2
дополнительных взаимно ортогональных распределения – горизонтальное ![]() и вертикальное
и вертикальное ![]() размерностей p и q
соответственно:
размерностей p и q
соответственно: ![]() ,
, ![]() . Обозначим h и v операторы проектирования на H и V соответственно.
Тогда
. Обозначим h и v операторы проектирования на H и V соответственно.
Тогда ![]() ,
, ![]() ,
, ![]() ,
, ![]() , и условие (2) можно представить в виде:
, и условие (2) можно представить в виде:
< X, Y >
= < hX, hY > + < vX, vY >. (3)
В
[2] Навейра выделил 64 класса римановых
структур почти произведения. В его работе рассматривается симметричное дважды
ковариантное тензорное поле Ф,
которое для любых векторных полей ![]() на
на ![]() определяется
следующим образом:
определяется
следующим образом: ![]() .
.
Пусть ![]() - связность
Леви-Чивита метрики g.
- связность
Леви-Чивита метрики g.
Ковариантная производная ![]() есть тензорное поле
типа (0,3)
есть тензорное поле
типа (0,3)
![]()
обладающее следующими свойствами:
1)![]() (4)
(4)
2)![]() (5)
(5)
Так как свойства ![]() выполняются на каждом
касательном пространстве, то можно смоделировать общую ситуацию на n-мерном векторном пространстве Т с двумя подпространствами
H и V
размерностей p и q соответственно,
выполняются на каждом
касательном пространстве, то можно смоделировать общую ситуацию на n-мерном векторном пространстве Т с двумя подпространствами
H и V
размерностей p и q соответственно, ![]() p + q = n. Пусть
p + q = n. Пусть ![]() - дуальное
пространство, и W – конечномерное пространство тензоров, обладающих
свойствами (4) и (5):
- дуальное
пространство, и W – конечномерное пространство тензоров, обладающих
свойствами (4) и (5):
![]() для
для ![]() .
.
Пусть ![]() - группа движений Т, оставляющих инвариантными подпространства
H и V. Каждому
элементу этой группы соответствует линейное преобразование в пространстве W . Данное
соответствие является представлением группы. Пространство W допускает
разложение на инвариантные и неприводимые компоненты при естественном представлении
группы
- группа движений Т, оставляющих инвариантными подпространства
H и V. Каждому
элементу этой группы соответствует линейное преобразование в пространстве W . Данное
соответствие является представлением группы. Пространство W допускает
разложение на инвариантные и неприводимые компоненты при естественном представлении
группы ![]() :
:
![]()
где ![]() и
и ![]()
![]() - ортогональные
подпространства,
- ортогональные
подпространства, ![]() ,
,
![]() ,
,
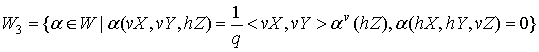 ,
,
![]() ,
,
![]() ,
,
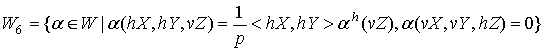 .
.
Здесь ![]() - ортонормированный
базис T такой, что
- ортонормированный
базис T такой, что
![]() ,
,
(![]()
![]() ), и для любого
), и для любого ![]() и любого
и любого ![]() :
:
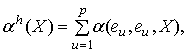
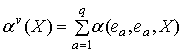
Поскольку ![]() , имеем 6 основных классов
, имеем 6 основных классов ![]() Другие классы могут
быть получены как прямая сумма элементарных классов:
Другие классы могут
быть получены как прямая сумма элементарных классов: ![]() , где
, где ![]() есть некоторое
подмножество (возможно пустое) множества
есть некоторое
подмножество (возможно пустое) множества ![]()
Навейра
сформулировал инвариантные характеристики классов в виде условий, накладываемых
на распределения ![]() и
и ![]() . Для любых
. Для любых ![]() (соответственно
(соответственно ![]() и любого
и любого ![]() горизонтальное
(соответственно вертикальное) распределение может удовлетворять следующим условиям:
горизонтальное
(соответственно вертикальное) распределение может удовлетворять следующим условиям:
![]() :
: ![]() - интегрируемое
распределение;
- интегрируемое
распределение;
![]() :
: ![]() - антислоение;
- антислоение;
![]() :
: ![]() - вполне
геодезическое слоение;
- вполне
геодезическое слоение;
![]() :
: ![]() (соответственно
(соответственно ![]() ) - распределение типа
) - распределение типа ![]() ,
,
![]() :
: ![]() - распределение типа
- распределение типа ![]() ,
,
(соответственно ![]() ),
),
![]() :
: 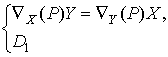 - минимальное
слоение,
- минимальное
слоение,
![]() :
: 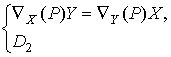 - вполне омбилическое
слоение.
- вполне омбилическое
слоение.
В [1] рассмотрен геометрический смысл данных
условий.
2. Рассмотрим
касательное расслоение ![]() гладкого n-мерного многообразия
гладкого n-мерного многообразия ![]() . Пусть
. Пусть ![]() - локальные
координаты на
- локальные
координаты на ![]() ,
, ![]() - естественные локальные координаты на
- естественные локальные координаты на ![]() . Здесь и далее
. Здесь и далее ![]()
![]() Пусть N – инфинитезимальная связность, с коэффициентами
Пусть N – инфинитезимальная связность, с коэффициентами ![]() , определяющая
горизонтальное распределение
, определяющая
горизонтальное распределение ![]() и, следовательно,
структуру почти произведения на
и, следовательно,
структуру почти произведения на ![]() : в каждой точке
: в каждой точке ![]()
![]() ,
,
где ![]() - вертикальное распределение, касающееся слоев.
- вертикальное распределение, касающееся слоев.
Векторные поля ![]() , образуют локальный базис
векторных полей, адаптированный к структуре почти произведения, где
, образуют локальный базис
векторных полей, адаптированный к структуре почти произведения, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Структурные уравнения имеют вид
. Структурные уравнения имеют вид
![]() ,
, ![]() ,
, ![]() , (6)
, (6)
где ![]() ,
, ![]() (
(![]() ).
).
Рассмотрим на ![]() риманову метрику
риманову метрику ![]() . Из (3) следует, что риманова метрика
. Из (3) следует, что риманова метрика ![]() является метрикой
структуры почти произведения тогда и только тогда, когда ее матрица в
адаптированных к структуре почти произведения координатах имеет
блочно-диагональный вид:
является метрикой
структуры почти произведения тогда и только тогда, когда ее матрица в
адаптированных к структуре почти произведения координатах имеет
блочно-диагональный вид:
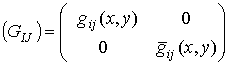 . (7)
. (7)
Вычисляя коэффициенты связности Леви-Чивита ![]() метрики
метрики ![]() , определяемые разложением
, определяемые разложением ![]() , находим:
, находим:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где ![]()
![]()
![]()
![]()
Рассмотрим специальный ортонормированный локальный
базис ![]() векторных полей на TM такой,
что
векторных полей на TM такой,
что ![]() ,
, ![]() . Векторные поля
. Векторные поля ![]() можно разложить по
векторным полям адаптированного базиса
можно разложить по
векторным полям адаптированного базиса ![]() :
: ![]() ,
, ![]() , где
, где ![]() ,
, ![]() ,
, ![]() и
и ![]()
![]()
Анализируя условия ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для каждого из распределений
в адаптированных к структуре почти
произведения координатах, и учитывая выражения, полученные для коэффициентов
связности Леви-Чивита метрики
для каждого из распределений
в адаптированных к структуре почти
произведения координатах, и учитывая выражения, полученные для коэффициентов
связности Леви-Чивита метрики ![]() , приходим к результатам, представленным в таблице. Инвариантные
характеристики всех классов Навейра могут быть получены объединением
соответствующих условий.
, приходим к результатам, представленным в таблице. Инвариантные
характеристики всех классов Навейра могут быть получены объединением
соответствующих условий.
|
|
Условия на H |
Условия на V |
|
|
|
Выполняется
тождественно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условия ![]() и
и ![]() ,
, ![]() и
и ![]() ,
, ![]() и
и ![]() для вертикального распределения V совпадают
в силу интегрируемости распределения V.
для вертикального распределения V совпадают
в силу интегрируемости распределения V.
Литература.
1. Gil-Medrano O. Geometries
properties of some classes of Riemannian almost-product manifolds. //
“Rend.Circ.mat.Palermo.”, 1983, 32, №3. – с.315-329.
2. Naveira, A.M. A
classification of Riemannian almost-product manifolds. // “Rend.mat.appl.”,
1983, 3, №3. – с.577-592.
3.
Сухова О.В. О некоторых классах Навейра римановых структур почти
произведения на касательном расслоении гладкого многообразия. // Вестник
Чувашского гос. пед. ун-та им. И.Я. Яковлева. // ГОУ ВПО Чувашский гос.
пед. ун-т им. И.Я. Яковлева. – 2006г. - №5(52). – С. 175-179.