ӘОЖ 51 (075) Математика/Прикладная математика
доцент, ф.-м.ғ.к. Ысмағұл Р.С.,
Математика
мамандығының студенті Қусайын О.
А.Байтұрсынов ат. Қостанай мемлекеттік
университеті
Реккуренттік формулалардың қолданылуы
Рекурренттік есептеудің жалпы проблемасы болып рекурсивті
функцияның теориясы табылады.
Рекурренттік
формула деп – әрбір 
тізбектерінің
мүшелерін 
алдыңғы
мүшемен өрнектейтін 
түріндегі
формула аталады.
Рекуренттік
формулалардың қолдануларының мысалдары
Натурал санның факториалын
есептеу: 
болғанда 
.
Фибоначчи санын есептеу мына формулалармен
беріледі:
.
түріндегі
интегралды есептеу 
.
Бессель
теңдеуінің дифференциалдық шешімі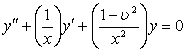 
дәрежелік қатар түрінде жазылуы мүмкін: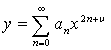 
.
Бұндағы 
коэффициентін анықтау үшін 
құру
жеткілікті. Осыдан кейін келесі нәтиже алынады: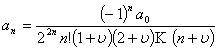 
.
Берілген
дұрыс көпбұрыштың екі еселегендегі
қабырғалар санының
қабырғалар ұзындығы: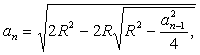 
мұндағы 
берілген
шеңбердің радиусы.
Сызықтық рекуренттік
тізбектердің оның характеристикалық
көпмүшесінің
түбірінен жалпы мүшесін өрнектейтін формула бар.
Фибоначчи тізбектері үшін осындай формула Бине формуласы болып табылады.
1 Рекурсивті
функция
Рекурсивті функция (лат. recursio
– қайту) – бұл 
сандық
аргументінің сандық функциясы. Мұндай жазу 
негізгі мәнінде
мәнін есептеуге
рұқсат береді, нақтырақ айтсақ индукция бойынша
белгілеу. Кез келген 
үшін функция
рекурсивті емес анықталуы қажетті (мысалы, 
үшін). Берілген
Фибоначчи
санының рекурсивті функциясының мысалы:
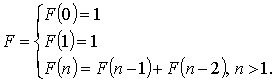
Осы жазуларды жаза келе, кез келген натурал 
үшін
қадамның ақырлы санын 
– ді есептей аламыз.
Қосымша 
мәнін есептеу
керек. Осы шығыстармен байланысында рекурсивті функцияның
рекурсивті емес (тұйық) тұлғасы бар болуын білу
қажет.
Мысалы,
рекурсивті функциясы 
тұйық
тұлғаға ауысуы мүмкін. Тұйық
тұлға барлық рекурсивті функциялар (қатынас) үшін
емес. Олардың ішінен кейбіреуі үшін тек жуықталған
тұйық тұлғалар табылады. Кейбір рекурсивті қатынастар, факториал сияқты
қатынастар элементар математикалық операциялар болып есептеледі.
Рекурсивті
құрылымын иеленетін көптеген алгоритмдер сияқты
рекурсивті функциялар алгортмдер теориясында маңызды роль атқарады.
2. Бине формуласы
Бине формуласы нақты
түрде 
мәні 
функциясынан: 
−алтын
қимасы. Осыдан 
және 
квадрат
теңдеудің 
түбірлері болып
табылады.
Бине формуласынан 
барлығы
үшін, 
барлығына
жақын бүтін сан бар, яғни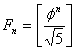 
. Келесі ассимптотикалық 
~
әділетті. Бине формуласы келесі аналитикалық
түрде кеңейтілген болуы мүмкін:
.
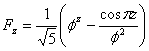қатынасы кез
келген 
комплекс саны
үшін орындалады.
3. Теңбе – теңдіктер
▪ 
▪ 
▪ 
▪ 
▪ 
▪ 
▪ 
▪ 
Көптеген жалпы формулалар:
▪ 
▪ 
▪ 
Фибоначчи
сандары бірліктер жиынтығында континуант мәнінен беріледі: 
яғни, сондай –
ақ, 
өлшемді
матрицасы болғанда, 
жорамал бірлік
болады. Фибоначчи сандарын Чебышев көпмүшеліктерімен
өрнектеуге болады:
Кез келген 
үшін, анықтауыштарды
есептеуде 
формуласы
қолданылады
Әдебиет:
1. А.И.Маркушевич. Возвратные
последовательности. – Гос.издательство технико – теоретической литературы,
1950. – Т.1. (Популярные лекции по математике).