Козлова О.В.
Лесосибирский педагогический институт –
филиал ФГАОУ ВПО «Сибирский федеральный университет», Лесосибирск
Площади многоугольников
Площади многоугольников
является неотъемлемой частью школьного курса математики, что вполне
естественно. Ведь исторически само возникновение геометрии связано с
потребностью сравнения земельных участков той или иной формы. Вместе с тем
следует отметить, что образовательные возможности раскрытия этой темы в средней
школе используются далеко не полностью.
Основная задача обучения
математике в школе заключается в обеспечении прочного и сознательного овладения
учащимися системой математических знаний и умений, необходимых в повседневной
жизни и трудовой деятельности каждому члену современного общества, достаточных
для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной
задачи углубленное изучение математики предусматривает формирование у учащихся
устойчивого интереса к предмету, выявление и развитие их математических
способностей, ориентацию на профессии, существенным образом связанные с
математикой, подготовку к обучению в вузе [2].
Площадь
многоугольника понимается как часть плоскости, ограниченная простой замкнутой
ломаной. В этом смысле понятие «многоугольник» используется в дальнейшем в
изложении школьного курса математики, а площадь многоугольника определяется с
помощью указания её свойств [1]:
1)
численное значение площади любого многоугольника всегда положительно;
2)
площади равных многоугольников, т. е. многоугольников, которые можно совместить
с помощью движения, одинаковы;
3)
площадь многоугольника, полученного объединением двух многоугольников, не
имеющих общих внутренних точек, будем называть не перекрывающимися);
4)
площадь квадрата со стороной единичной длины равна единице.
Рассмотрим основные теоремы о
площади многоугольника в курсе геометрии полной средней школы [3].
Теорема 1. Площадь треугольника равна половине произведения
его основания на высоту. 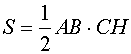
Формулы Герона для площади
треугольника.
![]() , где a, b, c – длины сторон треугольника, γ – угол, противолежащий стороне с;
, где a, b, c – длины сторон треугольника, γ – угол, противолежащий стороне с;
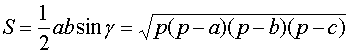 .
.
Теорема 2. Площадь
прямоугольника равна произведению его смежных сторон. ![]() .
.
Теорема
3. Площадь трапеции равна произведению полусуммы ее оснований на высоту. S = ((AD + BC)/2)*BH, где ВН - высота
трапеции.
Формула площади произвольного четырёхугольника с
диагоналями ![]() ,
, ![]() и углом
и углом ![]() между ними (или их продолжениями).
между ними (или их продолжениями). ![]()
Формулы площади произвольного
выпуклого четырёхугольника.
![]() , где
, где ![]() ,
, ![]() — длины диагоналей, a, b, c, d — длины
сторон.
— длины диагоналей, a, b, c, d — длины
сторон.
![]() , где
, где
p —полупериметр.
Существуют
особые случаи нахождения площадей четырехугольника.
Если
четырехугольник и вписан, и описан, то ![]() .
.
Следствие
1. Площадь произвольного четырёхугольника, вписанного в окружность, вычисляется
по формуле:
![]() .
.
Следствие
2. Площадь произвольного четырёхугольника, описанного около окружности,
вычисляется по формуле:
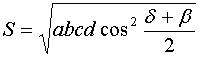 .
.
Следствие
3. Площадь четырёхугольника, вписанного в окружность и описанного около
окружности, может быть вычислена по формуле:
![]()
Таким образом, основная
сложность изучения материалам состоит в том, что не существует единого
универсального метода в нахождении площади многоугольника. Особое внимание в
работе с учащимися, необходимо уделять выводам формул площадей многоугольников,
которые позволяют развивать у учащихся аналитическое, логическое мышление,
применять такие умения, как умение анализировать, конкретизировать, обобщать.
1.
Атанасян, Л. С.
Геометрия 7-9. Учебник для общеобразовательных учреждений. – М.: Просвещение,
2000.
2.
Корешкова, Т. А.,
Цукерман, В. В. Многоугольники и их площадь в школьном курсе математики //
Математика в школе. – 2003. – №9. – С.10-18.
3.
Макарова, Н. Д. Площадь.
Единицы площади // Математика. – 2002. – №10. – С.30-31.