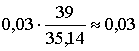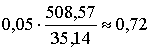Педагогические науки/5.Современные методы преподавания

К.т.н. Куимова Е.И., к.п.н. Ячинова С.Н.

Пензенский государственный университет архитектуры и строительства, Россия

О некоторых особенностях преподавания курса «Эконометрика»

В последние годы в курс обучения студентов, обучающихся по направлению «Менеджмент» и «Экономика» была введена новая дисциплина «Эконометрика», отвечающая за профессиональную подготовку будущего менеджера и экономиста. В России эконометрические методы известны сравнительно мало. Поэтому возникают трудности, заключающиеся в недостаточном количестве литературы, способствующей формированию у студентов навыков практического применения теоретических основ эконометрического моделирования. Кроме того, успешность изучения курса зависит от уровня освоения смежных дисциплин: экономической теории, математической экономики, экономической статистики, математической статистики и теории вероятностей. Для решения указанных выше задач при изучении курса «Эконометрика» используются лекционная и лабораторная формы занятий.

Курс лекций делится на два блока. Основной целью лекций, составляющих первый блок, является повторение основных теоретических сведений из математической статистики и теории вероятностей. Лекции, составляющие второй блок, ориентированы на овладение: терминологией, методологическими основами эконометрического моделирования; принципами и методами построения эконометрических моделей на основе пространственных данных и временных рядов; методикой оценки статистической значимости полученных результатов моделирования; принципами решения типовых задач в условиях мультиколлинеарности и автокорреляции.

Целью лабораторных работ является овладение студентами методами статистического анализа конкретных экономических данных. Материал каждой темы содержит справочную информацию по расчетным формулам, используемым при выполнении заданий, примеры выполнения типовых задач, контрольные задания для выполнения самостоятельной работы. В заданиях предусмотрена не только параметризация модели, но и содержательная интерпретация результатов эконометрического моделирования. Задания лабораторных работ выполняются с привлечением возможностей MS Excel.

Рассмотрим практические рекомендации по выполнению расчетов с помощью табличного редактора MS Excel.

Исследуется зависимость производительности труда y (т/ч) от уровня механизации работ (%), среднего возраста работников (лет) и энерговооруженности (кВт/100 работающих) по данным 14 промышленных предприятий.

	32	30	36	40	41	47	56	54	60	55	61	67	69	76
	33	31	41	39	46	43	34	38	42	35	39	44	40	41
	300	290	350	400	400	480	500	520	590	540	600	700	700	750
y	20	24	28	30	31	33	34	37	38	40	41	43	45	48

1. Получение протокола расчета. Операция проводится с помощью инструмента Анализ данных/Регрессия. Она аналогична расчету параметров парной линейной регрессии, рассмотренной выше, только в отличие от парной регрессии при заполнении строки входной интервал X в диалоговом окне следует указать сразу все столбцы значений факторных переменных.

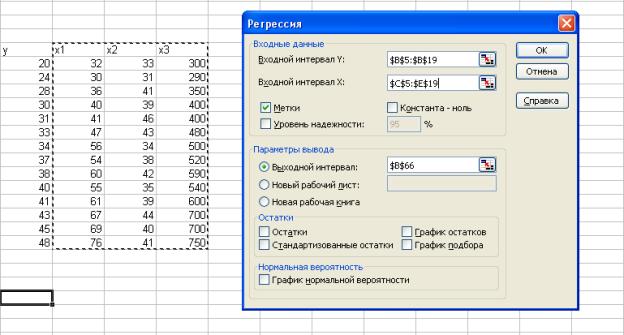
Результаты анализа имеют вид:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,97517313
R-квадрат	0,950962633
Нормированный R-квадрат	0,936251423
Стандартная ошибка	2,038864298
Наблюдения	14
Дисперсионный анализ
	df	SS	MS	F
Регрессия	3	806,1446094	268,7148698	64,64204
Остаток	10	41,56967627	4,156967627
Итого	13	847,7142857
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	5,711742473	6,18918556	0,922858495
x1	0,148601283	0,340417689	0,436526326
x2	0,064880259	0,162051974	0,400366976
x3	0,037784221	0,033824423	1,11706919

2. Оцениваем статистическую значимость в целом. Изучив результаты, отмечаем, что в целом полученное уравнение линейной множественной регрессии

является статистически значимым. Действительно, . Сравним это число с критическим значением критерия Фишера, полученным при числе степеней свободы и , где n – число наблюдений, m – число параметров при переменной x. В нашем случае , . Критическое значение даст функция FРАСПОБР. , что существенно меньше расчетного значения.

О доле вариации результативного признака y, объясненной построенным уравнением множественной регрессии лучше всего судить по значению нормированного коэффициента корреляции, в данном случае он равен 0,9363. То есть построенное уравнение объясняет почти 94% всей вариации признака y.

3. Оцениваем статистическую значимость по отдельным параметрам. Чтобы оценить статистическую значимость параметров регрессионной модели с помощью t-критерия, найдем соответствующее нашим параметрам критическое значение с помощью функции СТЬЮДРАСПОБР при заданном уровне значимости 0,05 и числе степеней свободы . Коэффициент признается значимым, если выполняется неравенство . Имеем

	0,44	0,4	1,12
	2,2281

Таким образом, ни один из факторов не имеет статистически значимого коэффициента регрессии, и построенное уравнение для прогнозирования непригодно.

4. Исследуем коллинеарность между факторами. Матрицу парных коэффициентов корреляции можно получить, используя инструмент Анализ данных/Корреляция. Заполнив диалоговое окно,

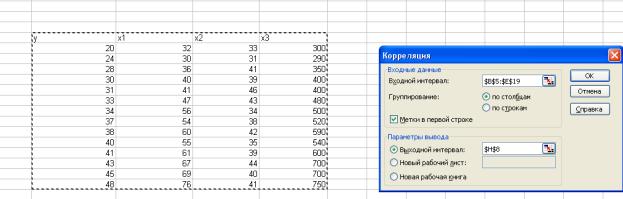
получим следующий результат:

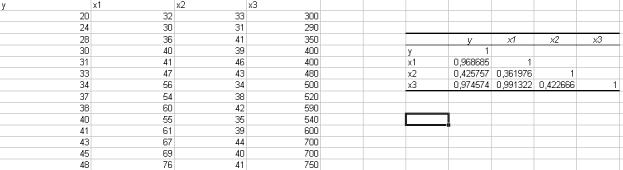
Для оценки мультиколлинеарности факторов вычислим определитель матрицы парных коэффициентов корреляции факторов.

.

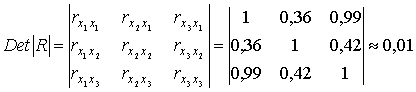Поскольку определитель матрицы межфакторной корреляции близок к нулю, имеем мультиколлинеарность факторов и вытекающую отсюда ненадежность результатов множественной регрессии.

Особенно высока коллинеарность факторов и , . Один из этих факторов следует исключить из уравнения регрессии. Логично исключить тот, который имеет меньший коэффициент парной корреляции. Поскольку , а , исключаем фактор .

5. Построим регрессию на факторах и .

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,974693901
R-квадрат	0,950028201
Нормированный R-квадрат	0,940942419
Стандартная ошибка	1,962415214
Наблюдения	14
Дисперсионный анализ
	df	SS	MS	F
Регрессия	2	805,3524775	402,6762388	104,5621
Остаток	11	42,3618082	3,851073473
Итого	13	847,7142857
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	7,265656067	4,873196972	1,490942416
x2	0,031021017	0,136948082	0,226516625
x3	0,052435862	0,004030875	13,00855684

Получили результаты:

, , , что много больше, чем .

	0,22	13
	2,2281

Таким образом, при весьма удовлетворительной значимости уравнения регрессии в целом, мы добились значимости коэффициента регрессии при переменной .

6.а) Найдем коэффициенты эластичности: ,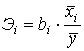

где – коэффициент «чистой» регрессии при факторе ;

– среднее значение результативного признака;

– среднее значение признака .

Имеем

	y
Среднее	35,14285714	39	508,5714286
Эластичность

Таким образом, при изменении фактора (среднего возраста работников) на 1%, производительность возрастает незначительно, на 0,03%; при изменении фактора (энерговооруженности) на 1%, производительность труда увеличивается на 0,72%.

б) Выполним прогнозирование. Прогнозные значения факторов:

; . Тогда .

в) Доверительный интервал для данного прогнозного значения y можно найти, зная предельную ошибку прогноза , где – соответствующее критическое значение критерия Стьюдента, а – ошибка прогнозного значения. В нашем случае .

Ошибку прогнозного значения функции регрессии получим по формуле

.

Шаг 1. Параметр S – стандартная ошибка регрессии приведен в последней регрессионной статистике .

Шаг 2. Матрица состоит из чисел: .

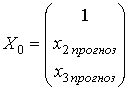То есть , .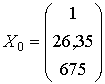

Шаг 3. Матрица X состоит из чисел .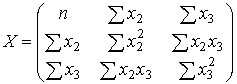

Составляем вспомогательную таблицу:

	…..	…..	….	…..	…..
Сумма

В данном случае, .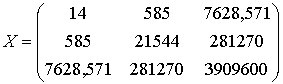

Шаг 4. Транспонируем матрицу X. Поскольку она симметрическая, то

.

Шаг 5. Найдем произведение матриц . В Exсel это можно сделать с помощью функции МУМНОЖ.

	58537523,04	2158299716	29989312607
	2158299716	79577299061	1,10572E+12
	29989312607	1,10572E+12	1,53641E+13

Шаг 6. Найдем обратную матрицу к матрице произведения . В Exсel это можно сделать с помощью функции МОБР.

	0,281568563	-0,007773123	9,81695E-06
	-0,007773123	0,000215175	-3,13231E-07
	9,81695E-06	-3,13231E-07	3,38079E-09

Шаг 7. Найдем произведение матриц (размерность матрицы произведения ).

0,083373216

-0,002314683

3,84533E-06

Шаг 8. Найдем произведение матриц (размерность матрицы произведения , то есть только одно число).

.

Шаг 9. .

Шаг 10. .

Шаг 11. Таким образом, прогнозное значение результата будет с вероятностью 95% находиться в интервале .

Таким образом, выполнение лабораторных работ способствует повышению уровня освоения учебного материала, так как привлечение возможностей MS Excel позволяет, с одной стороны, «прочувствовать» все детали и тонкости изучаемых методов, а с другой – совершенствовать навыки работы в пакете MS Excel, необходимые для работы экономиста.