И.А. Долгарев и А.И. Долгарев

ГЕОМЕТРИЯ ГАЛИЛЕЕВЫХ ДВИЖЕНИЙ

В СРАВНЕНИИ С ГЕОМЕТРИЕЙ ПАРАЛЛЕЛЬНЫХ ПЕРЕНОСОВ

Основой евклидовой геометрии служит линейное пространство параллельных переносов. Рассматривая галилеевы преобразования, приходим к некоммутативному галилееву пространству-времени, пространственная составляющая которого евклидова. При изучении движения материальных объектов в евклидовой плоскости методами евклидовой геометрии и методами некоммутативной галилеевой геометрии, получаем различные результаты. Скорости движений в некоммутативном пространстве-времени замедляются или увеличиваются по сравнению со скоростями в евклидовом пространстве.

На многообразии определены различные геометрии. Тройку можно считать параллельным переносом аффинного пространства. В этом случае на определяется линейное пространство над полем действительных чисел в результате задания следующих операций

(1) , , .

Параллельные переносы еще называются векторами. Тройку можно считать точкой и обозначать многообразие через . В отображении всякой паре точек соответствует параллельный перенос из ; соответствие записывается в виде равенства . Считается, что отображение удовлетворяет известным аксиомам Г. Вейля аффинного пространства, [1, c. 27 – 28]. Если , , то отображение задается равенством

(2) .

Далее на многообразии можно развивать аффинную геометрию.

На многообразии определяются и другие операции, например,

(3) ,

см. [2]. Введя соответствующую внешнюю операцию, получаем алгебраическую структуру, альтернативную структуре . В аксиоматике Г. Вейля на этой структуре строится своя геометрия. Сложение троек в (1) коммутативно и линейно, сложение (3) коммутативно и нелинейно. Ниже, в п. 4, приведен пример некоммутативной операции на .

1. Траектории точек в параллельных переносах

Пусть в ненулевом параллельном переносе аффинного пространства точка отображается на точку . Формулы параллельного переноса :

.

Взяв кратное параллельного переноса , имеем параллельный перенос . Множество образов точки в параллельных переносах , , является прямой линией аффинного пространства , эту прямую можно описать векторной функцией

(4) .

Прямая является траекторией точки в параллельном переносе . Прямые и параллельны, прямые и при имеют не более одной общей точки.

Геометрия линейного пространства параллельных переносов является аффинной. На ее основе получаются другие геометрии в результате введения скалярного произведения векторов.

2. О евклидовой геометрии

Определяя евклидово скалярное произведение векторов в , получаем евклидово векторное пространство , при этом аффинное пространство превращается в евклидово пространство . Евклидова норма вектора определяется равенством ,

.

Евклидово расстояние между точками и , на основе (2), равно

(5) .

Евклидова траектория точки в параллельном переносе остается такой же, как в аффинном пространстве. Норма векторов позволяет дифференцировать векторные функции. Если функция

(6) =

непрерывна на некотором интервале, то ее производная есть

(7) =.

Траектория (6), где имеет смысл времени, считается регулярной класса . Вектор скорости, движущейся по траектории (6) точки, равен . Выполняются следующие утверждения.

1. СВОЙСТВО. В каждой компоненте производной имеется зависимость только от этой компоненты и нет зависимости от других компонент .

2. СВОЙСТВО. В движении по прямолинейной траектории (4) , вектор скорости точки постоянен, вектор ускорения равен .

# Производная функции (4) есть постоянный вектор: =. Ускорение . Ускорение в движении по траектории (4) отсутствует. #

Свойства движений материальных точек по евклидовым траекториям изучает, в том числе, и евклидова геометрия.

3. Геометрия евклидовых движений

Формулы галилеевых движений, как известно, имеют вид

материальная точка с координатой на прямой, по которой она движется со скоростью , приходит в положение через промежуток времени . Начальные условия движения : . В движении событие отображается на событие . Пусть

еще одно галилеево движение. Композиция данных движений есть движение

эти формулы получены в результате подстановки формул в формулы . Каждому движению соответствует унитреугольная матрица, композиции движений соответствует произведение матриц движений, взятых в обратном порядке

(8) =.

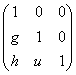
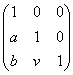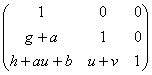Галилеевы движения составляют группу , она изоморфна унитреуголной группе , которая нильпотентна ступени 2. Имеется соответствие между матрицами из и тройками из :

(9) .

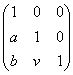
Произведению матриц в (8) соответствует операция над тройками из :

(10) = =,

где . Тождественному галилееву движению соответствует единичная матрица и, по (9), нулевая тройка ; противоположная к тройка такова

.

На группе троек с операцией сложения (10) введена внешняя операция умножения троек на действительные числа

(11) , ;

[3, с. 8 – 9] и [4, с. 113]. Внешняя операция на группе с внутренней операцией + умножение на числа из обозначается . Имеем алгебраическую структуру

;

она называется сибсоном, [3, с. 7] и [4, с. 107]; элементы сибсона называются сибсами. Сибсон обобщает линейное пространство над , относится к одулям Ли, [4, с. 102 – 103], которые выделяются из одулей над кольцом, определенными Л.В. Сабининым в [5]. Тем самым и на группе галилеевых движений определен сибсон.

По аналогии с аффинным пространством с линейным пространством параллельных переносов определяется одулярное пространство на сибсоне галилеевых движений: в векторной аксиоматике Г. Вейля аффинного пространства линейное пространство заменено сибсоном , [3, с. 11 – 16] и [4, с. 128 – 130]. Вейлевское одулярное пространство с сибсоном называется ЛС-пространством, это пространство галилеевых движений. Точками ЛС-пространства являются тройки действительных чисел. Паре точек соответствует сибс , пишем . Для любых трех точек выполняется условие: если , , то . Пусть , и начало отсчета. Выполняется соотношение = . Паре соответствует сибс

(12) ,

т.е., согласно (9), паре точек cоответствует галилеево движение

;

имеется геометрия пространства с сибсоном, [3, 4], – геометрия галилеевых движений.

4. Траектории сибсона галилеевых движений

По аналогии с аффинной прямой, п.1, определяется прямая ЛС-пространства . Через точку в направлении сибса проходит прямая , содержащая все точки , для которых , . Параметрические уравнения прямой :

(13) , , ,

см. [4, с. 166]. При уравнения прямой ЛС-пространства нелинейны, они содержат вторую степень параметра ; при уравнения (13) линейны. Прямые ЛС-пространства являются траекториями точек в галилеевых движениях. Положим в (13): , . Траекторию (13) зададим сибсонной функцией

(14) = .

В общем случае траектории точек в галилеевых движениях параболические. О траекториях сибсона, т.е. сетевых уравнениях сибсона см. [4, с. 250 – 251].

5. Дифференцирование сибсонных функций

На сибсоне вводится галилеева норма сибсов. Галилеевой нормой сибса , согласно [3, с. 11] и [4, с. 120 – 121], называется

(15)

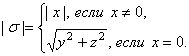
Это аналог галилеева расстояния между точками, см. [6, с. 843 – 844]. Пространство с нормированным сибсоном называется ЕС-пространством, обозначается и является галилеевым пространством-временем. Точки из называются событиями. Первые компоненты сибсов из и событий из считаются временными, вторые и третьи компоненты называются пространственными. Некоммутативное одулярное галилеево пространство с сибсоном является миром.

События и одновременны. По (12) имеем сибс

.

Согласно (15), сибс евклидов. Множество одновременных между собою событий мира является евклидовой плоскостью в ЕС-пространстве. Событие состоит в том, что точка из рассматривается в момент времени . Линия

(16) = ,

содержащая событие , называется мировой линией события , а проекция

=

мировой линии на евклидову плоскость пространства-времени является траекторией точки .

Рассматривается сибсонная функция (16). Если параметр получает приращение , то функция получает приращение . Отыскивается предел при условии . Вычисляется производная функции по формуле

(18) ,

см. [3, с. 18 – 20] и [4, с. 123 – 125]. В частности, производная функции

=, ,

равна

(19) .

Отметим в сравнении со свойством 2

3. СВОЙСТВО. В третьей, пространственной компоненте производной (18) сибсонной функции содержатся еще производная второй, тоже пространственной компоненты исходной функции и сама эта компонента.

6. Движение по траекториям галилеевых движений

Мировая линия (14) галилеева движения при описывается функцией

(20) =.

Траектория точки есть = . Производная функции (20) по (18) такова

= ,

значит, скорость движения по траектории в ЕС-пространстве определяется вектором

==.

Скорость постоянна. Ускорение движения находим, дифференцируя функцию по (19):

,

ускорение движения по траектории (20), как пространственная составляющая сибса является нулевым.

В евклидовой плоскости, не входящей в ЕС-пространство, по траектории точка движется со скоростью =, которая непостоянна. Таким образом, выполняется

4. СВОЙСТВО. По траекториям галилеевых движений, составляющих сибсон, материальная точка движется в ЕС-пространстве с постоянной скоростью и нулевым ускорением. В евклидовой плоскости, не входящей в ЕС-пространство, по траектории точка движется с изменяющейся скоростью.

7. Движение по параболической траектории другого вида

Рассмотрим мировую линию движения в ЕС-пространстве

(21) = .

Траектория этого движения в евклидовой плоскости ЕС-пространства:

=.

Для сравнения рассмотрим такую же траекторию

=

движения в евклидовой плоскости, не лежащей в ЕС-пространстве. Мировую линию скорости движения в ЕС-пространстве найдем по (19):

=.

В евклидовой плоскости ЕС-пространства вектор скорости движения есть

=.

Скорость движения в евклидовой геометрии такова

.

Установлена следующая

5. ТЕОРЕМА. Скорость движения в ЕС-пространстве-времени по мировой линии (21) отличается от скорости движения в евклидовом пространстве на величину в последней компоненте. При и в движении в ЕС-пространстве-времени происходит увеличении скорости по сравнению с движением по той же траектории, изучаемого методами евклидовой геометрии, и происходит уменьшении скорости при и .

8. Изучение движения различными методами

В книге [7, с. 11, подстрочное примечание], отмечается, что экспериментальные факты не подтверждают того, что механике Галилея-Ньютона соответствует рассматриваемая в книге геометрия Галилея (коммутативная и линейная).

6. ТЕОРЕМА. Если механике Галилея-Ньютона соответствует геометрия нильпотентного галилеева ЕС-пространства-времени, то в движениях с различными мировыми линиями по одним траекториям скорости движения со временем либо замедляются, либо увеличиваются, но они не совпадают, вообще говоря, со скоростями, вычисленными средствами евклидовой геометрии.

В движениях по различным траекториям в ЕС-пространстве-времени различны и изменения скорости по сравнению с движением по траекториям в пространстве с евклидовой геометрией. В дифференциальной геометрии ЕС-пространства-времени кривизна траекторий сибсона галилеевых движений, т.е прямых ЕС-пространства-времени, равна нулю, [3, 4]. Это соответствует смыслу прямых линий пространства-времени.

9. Соотношение между геометриями параллельных переносов

и галилеевых движений

Геометрия параллельных переносов является аффинной, она линейна и коммутативна. Преобразования аффинного пространства описываются линейными формулами, обладают матрицами, определители которых отличны от нуля. Всякое преобразование с такими свойствами является аффинным. Аффинная группа некоммутативна. Матрица аффинного преобразования галилеева порядка 3+1, ее первая строка есть (1 0 0 0). Галилеевы движения составляют подгруппу аффинной группы. Геометрия галилеевых движений некоммутативна, хотя и создана на подгруппе преобразований коммутативного аффинного пространства, в основе которого лежит коммутативная группа параллельных переносов.

Литература.

1. Вейль, Г. Пространство. Время. Материя. Лекции по общей теории относительности. – М.: Едиториал УРСС, 2004. – 456 с.
2. Долгарев А.И., Долгарев И.А. Альтернативное 2-мерное действительное линейное пространство. Группа Ли замен базисов пространства.// Владикавказский математический журнал, т. 10. вып. 2 (апрель-июль), Владикавказ, 2008, С. 9 – 20.
3. Долгарев А.И. Дифференциальная геометрия пространства с касательным отображением в одуль галилеевых движений. – Саранск: Средневолжское математическое общество, 2002, препринт 51. – 52с.
4. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005. – 306 с.
5. Сабинин Л.В. Одули как новый подход к геометрии со связностью // ДАН СССР. 1977. N5. C.800-803.
6. Математическая энциклопедия, Т.1. – М. Советская энциклопедия, 1977. – 1152с.
7. Арнольд В.И. Математические методы классической механики. – М.: Наука, 1989. – 472с.