УДК 539.3

Валишин А.А. д.ф.-м.н, проф.,  Миронова Т.С. аспирант.

Московский государственный университет тонких химических технологий им. М.В. Ломоносова. Россия.

Зона вынужденной эластичности перед трещиной разрушения в полимерах и композитах на их основе.

                                                         Аннотация.

  Квазихрупкое разрушение полимеров и композитов на их основе наблюдается в температурном диапазоне от температуры хрупкости до температуры стеклования. В этом случае перед фронтом трещины разрушения, которая является концентратором напряжения, возникают  неупругие деформации. В металлах – это пластические деформации, в полимернах – это вынужденноэластические деформации. В статье определены форма и размеры зоны вынужденной эластичности, возникающей в аморфных твердых полимерах перед трещиной разрушения при температурах выше температуры хрупкости.  В компьютерном эксперименте исследовано движение трещины с эластической зоной. Исследованы процессы тепловыделения при формировании зоны вынужденной эластичности.

       По принятой в литературе прочностной классификации твердые полимеры делятся на три типа: низкопрочные, высокопрочные и свехпрочные [1]. Разрушение низкопрочных материалов, о которых пойдет речь, происходит в результате роста наиболее опасной трещины вплоть или до полного разрушения  изделия или конструкции, или до достижения неприемлего уровня повреждения.

   Трещина в материале  растет под действием локальных напряжений в ее вершине. При этом неважно, каким фактором созданы эти локальные напряжения: внешним механическим напряжением,  неоднородным температурным полем или может быть каким-то другим фактором.

     Известно, что в механическом поле трещина является концентратором напряжения: локальные напряжения вблизи ее вершины многократно превышают напряжения вдали от нее. В температурном поле трещина является ещё и концентратором теплового потока: величина теплового потока и градиента температурного поля вблизи трещины много больше, чем вдали от нее [2].

    Реальная трещина представляет собой щель с асимптотически сходящимися берегами.  При этом расстояние между берегами (раскрытие трещины) плавно уменьшается вплоть до межчастичных расстояний (межатомных и межмолекулярных). Отсюда следует, что в концевой части трещины есть участок, где существенны силы межатомного и межмолекулярного взаимодействия берегов трещины [3-5]. Межчастичные силы сцепления вблизи кончика трещины обеспечивают плавное смыкание ее берегов и конечность напряжений вблизи ее вершины.

Кончик трещины представляет собой маленький «клюв». Форма трещины в области клюва, напряженное состояние клюва и  его размеры  полностью определяются силами межатомного и межмолекулярного взаимодействия и не зависят от внешних нагрузок и температуры. Иными словами, «клюв» трещины автономен по отношению ко всей трещине, и при росте последней перемещается впереди нее, не меняя ни своих размеров, ни формы [3,4,6].  В остальной части форма трещины зависит от внешних напряжений механического, термического  или иного происхождения.  Предельное значение размеров «клюва» определяется формулой.

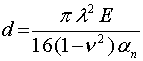                                                                                              (1)      

где -среднее межмолекулярное расстояние, которое определяет наибольшее раскрытие «клюва», -удельная поверхностная энергия разрушения, Е –модуль Юнга, -коэффициент Пуассона.  Для численной оценки размера «клюва» возьмем данные для ПММА [1]: , , , . Получаем     .  Сравним эти результаты с диаметром флуктуационного объема, в котором согласно термофлуктуационной теории разрушения [1] происходят элементарные акты разрушения.  Для ПММА в [1] приводятся значения  , отсюда диаметр флуктуационного объема будет , т.е. диаметр флуктуационного объема и длина «клюва» трещины практически одинаковы. Из этого совпадения следует, что «клюв» - это тот микрообъем вблизи трещины (флуктуационный объем), в котором разыгрываются элементарные акты разрушения.  Точнее, в этом микрообъеме происходят заключительные акты «дорывания» напряженных связей. Первичные же акты предразрушения происходят перед фронтом трещины в особых возникающих там условиях, где из-за больших напряжений развиваются неупругие явления.

      Напряжение сцепления в клюве трещины определяется формулой 

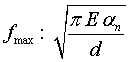                                                                                     (2)      

По этой формуле можно оценить порядок величины напряжения сцепления. Для ПММА возьмем численные данные из [1]: , . Получаем оценки  напряжения сцепления:,    .

 

Таким образом, напряжение в клюве трещины конечно и для ПММА его можно принять равным 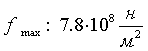. Для трещины нормального отрыва это нормальное напряжения . Что касается трещины поперечного сдвига (трещина второго типа), то здесь ее фронт продвигается путем скольжения берегов относительно друг друга. Поэтому напряжение сцепления в клюве этой трещины – это тангенциальное напряжение , хотя межчастичные связи при всяком виде макроскопических напряжений испытывают только растяжение.

     При фрактографическом исследовании поверхности излома разрушенных образцов наблюдались три зоны: зеркальная, матовая и перьевая (искромсанная) [1,9]. Зеркальная зона соответствует медленному флуктационному подрастанию трещины. Трещина на своем пути пересекает множество микрополостей размером от нескольких до десятка микрон. Взаимодействие трещины с этими микрополостями приводит к зарождению многих вторичных микротрещин, так что трещина разрушения продвигается как бы через заранее подготовленную разрыхленную среду, насыщенную микропорами и микротрещинами. В матовой зоне, соответствующей атермической  стадии движения трещины с большой скоростью, возросшие локальные напряжения становятся достаточными для активизации изолированных микрополостей и их взаимодействия. Здесь уже одновременно вместе с магистральной трещиной распространяется множество вторичных микротрещин. В перьевой зоне, которая завершает разрушение, этот процесс становится еще интенсивнее.

      Упомянутые процессы предразрушения, т.е накопление микроповреждений («разрыхление») перед фронтом трещины ,идут параллельно с развитием неупругой вынужденноэластической деформации. Процессы предразрушения и вынужденноэластического деформирования развиваются во времени с конечной скоростью.

            Наиболее известной теорией, учитывающей наличие неупругой зоны перед трещиной, является теория Леонова-Панасюка-Дагдейла (ЛПД) [5,7]. В этой теории рассматривается трещина нормального отрыва  с  пластической зоной перед ней. Теория ЛПД была создана для материалов, деформирующихся пластически, в первую очередь металлов.

Пластическая  зона моделируется тонкой прослойкой на продолжении трещины, заполненной нелинейно пластически деформированным материалом. 

     В полимерах внешним аналогом пластической деформации является вынужденноэластическая деформация. По внешним признакам эта деформация напоминает пластическую, хотя по физической природе это совершенно разные виды деформаций.  Поэтому перед фронтом трещины возникает зона вынужденноэлатической деформации.  Развитие вынужденной эластической деформации происходит с преодолением внутреннего трения и выделением тепла, что приводит к нагреванию материала вблизи трещины. Это, с одной стороны, ускоряет процесс накопления повреждений, а с другой – через релаксацию напряжения тормозит их. Микрорасслоение материала в эластической зоне, которое начинается, если температура зоны приближается к температуре стеклования, приводит к ориентационному упрочнению и так же затормаживает процессы предразрушения.

По достижении напряжения, равного пределу вынужденной эластичности  для данной температуры, «размораживается» сегментальная подвижность звеньев макромолекул и начинает развиваться вынужденная эластическая деформация ползучести при напряжении, связанная с разворачиванием свернутых конформаций макромолекул и с большими перемещениями материала внутри зоны вынужденной эластичности. Вне эластической зоны, где напряжения меньше предела вынужденной эластичности, сегментальная подвижность блокируется межмолекулярным взаимодействием, и одно только тепловое движение не в силах его преодолеть. Поэтому вне эластической зоны материал испытывают только малые упругие деформации.

Напряжение в эластической зоне конечно и равно пределу вынужденной эластичности, соответствующему данной локальной температуре зоны. Форма и размеры зоны вынужденной эластичности описываются в полярных координатах формулой

 

                                                                                (3)

Здесь - предел вынужденной эластичности, К-коэффициент интенсивности напряжений (К1 для тещины нормального отрыва и К2 для трещины поперечного сдвига).  

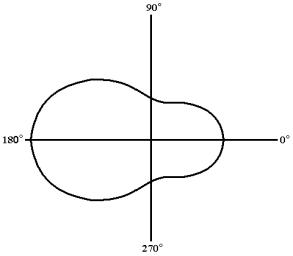
Рис. 1. Форма зоны вынужденной эластичности вблизи трещины поперечного сдвига при плоском напряженном состоянии.

На рис 1 представлена рассчитанная форма эластической зоны. Построение выполнено в безразмерных полярных координатах с использованием безразмерного полярного радиуса 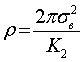. Большая часть эластической зоны вытянута вдоль берегов трещины. Примерно 20% эластической зоны располагается впереди перед фронтом трещины. Это «активная» часть эластической зоны, она является продолжением клюва трещины, именно здесь процессы предразрушения «прокладывают дорогу» для дальнейшего роста трещины.

       Площадь эластической зоны легко найти, проинтегрировав выражения (3) по области, ограниченной контуром зоны на рис 1. Получаем

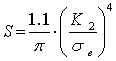                                                                                         (4)      

Площадь же «активной» части зоны равна

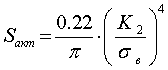                                                                            (5)      

Объем активной части получается умножением на толщину образца h:

                                                                                                    (6)          

Длина активной части зоны, находящейся перед фронтом трещины, равна 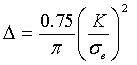                                                                                                                                     (7)      

Размеры эластической зоны, как видно из формул (4)-(7), полностью определяются соотношением между коэффициентами интенсивности напряжений (КИН) К и пределом вынужденной эластичности .   В определении размеров эластической зоны ведущую роль играет коэффициент интенсивности напряжений (КИН) К. Динамический КИН для движущейся трещины, вообще говоря, отличен от статического, и зависит от скорости трещины. В работе [8] для движущейся трещины нормального отрыва при постоянном одноосном растягивающем напряжении получено выражение для динамического КИН  К в виде

                                                             (8)                  

Здесь - статический КИН, рассчитываемый обычными методами механики разрушения, а  - динамическая поправка, равная

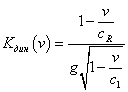                                                                               (9)             

где фактор g слабо зависит от скорости трещины  и принимает значения, близкие к единице, - скорость поверхностных рэлеевских волн, а - скорость продольных упругих волн расширения-сжатия . С увеличением скорости трещины  динамическая поправка  уменьшается, стремясь к нулю при . Эксперименты показывают, что максимальная скорость трещины не достигает рэлеевской скорости   и по различным данным составляет   . [9,10].

    По мере роста трещины увеличивается статический КИН, и размеры эластической зоны тоже увеличиваются, т.к. на больших расстояниях от фронта трещины напряжения достигают предела вынужденной эластичности . При увеличении локальной температуры вблизи трещины уменьшается предел вынужденной эластичности , и опять раньше, т.е. на больших расстояниях напряжения достигают этого предела. Поэтому размеры эластической зоны увеличиваются с ростом локальной температуры. Поскольку локальная температура тоже зависит от длины трещины, то, в конечном счете, при заданных внешних условиях размеры эластической зоны управляются размером трещины.

      Если локальная температура вблизи фронта трещины выше температуры хрупкости, то здесь начинает развиваться вынужденная эластическая деформация и появляется эластическая зона, размеры которой сокращаются с уменьшением локальной температуры и при температуре хрупкости  эластическая зона стягивается к клюву трещины. Поэтому при температурах ниже температуры хрупкости трещина растет по хрупкому механизму без эластической зоны. Начиная же с температуры квазихрупкости , в эластической зоне появляется собственная структура: материал зоны расслаивается на тяжи, отделенные друг от друга и зона преобразуется в крейз (трещину серебра). Для справки приведем значения этих эпюрных температур для двух полимеров, взятые из монографии [1]:

ПММА  ,  ,  

ПЭТФ ,  ,    

Если локальная температура выше  или становиться таковой в процессе медленного подрастания трещины, то перед ее фронтом появляется эластическая зона, и трещина прорастает через нее, одновременно двигая ее вперед.

    Для аморфных полимеров, таких как ПММА, ПС, ПЭТФ и др. ниже температуры стеклования  выделяются при прочностных состояния: хрупкое, квазихрупкое и нехрупкое (вязкоупругое) [1]. Они разделяются температурами хрупкости и квазихрупкости . В каждом состоянии распространение трещины имеет свою специфику, что отражено в названиях трещин: хрупкая, квазихрупкая и трещина серебра (крейз).  Ниже  реализуется хрупкая трещина без эластической зоны, в интервале от   до  перед фронтом трещины появляется эластическая зона, а выше  она преобразуется в крейз и трещина прорастает через него за счет накопления  в тяжах повреждений и их последующего разрыва. 

          В работе [11]   отмечается, что для развития в пластичных материалах (в первую очередь, в металлах) хрупкого или нехрупкого разрушения важную роль играет скорость трещины. Пока скорость мала пластическая деформация успевает развиться, и трещина растет через пластическую зону. Когда же скорость достигает достаточно большой величины, пластическая деформация не успевает за трещиной и наступает хрупкий разрыв, который затем может снова превратится в пластический, если освобождающейся упругой энергии окажется недостаточно для обеспечения нужной скорости трещины. Этот релаксационный фактор еще в большей степени проявляется в полимерах, которые в отношении механических свойств являются вязкоупругими средами с сильной зависимостью механических характеристик от скорости и длительности (и частоты) воздействия, а также от температуры.

    «Проигрывание» на компьютере движения трещины в условиях существования впереди неё зоны вынужденной эластичности приводит к следующим результатам. Вынужденная эластическая деформация развивается во времени с конечной скоростью, зависящей от напряжения и температуры. Скорость формирования эластической зоны характеризуется временем запаздывания вынужденной эластической деформации ползучести t, зависящим от интенсивности межмолекулярных взаимодействий, тормозящих процесс разворачивания свернутых конформаций макромолекул, а также от температуры и внешнего напряжения. Ведем безразмерный характеристический параметр 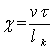 , где - скорость трещины, а - ее критическая длина на флуктационной стадии движения. Произведение  определяет среднее расстояние, на которое продвинулась бы трещина за время развития вынужденной эластичности деформации . Если  то это означает, что за время  трещина прошла бы путь, много меньший ее критического пути, т.е. подавляющую часть своего пути трещина будет двигаться в условиях уже развившейся вынужденной эластической деформации впереди нее. Поэтому условия  определяет наличие перед трещиной сформировавшейся зоны вынужденной эластичности.

Развитие вынужденной эластической деформации происходит с совершением работы против сил внутреннего трения и сопровождается выделением тепла. Можно показать, что пока скорость трещины невелика это тепло успевает отводится во вне, и движение трещины является изотермическим.

По мере роста трещины ее скорость возрастает, напряжения вблизи ее фронта увеличиваются, выделяющиеся тепло уже не успевает полностью отводится, и происходит постепенный переход к адиабатическому движению трещины, эластическая зона нагревается, увеличивается частота элементарных актов разрушения, время развития вынужденной эластической деформации уменьшается, уменьшается и предел вынужденной эластичности . Все эти факторы противоречивым образом влияют на движение трещины и эволюцию эластической зоны. В конце медленной стадии движения трещины из-за адиабатического разогрева ее скорость резко, почти скачком увеличивается, приближаясь к предельной скорости атермической стадии. В это время характеристический параметр  становится больше единицы, и вынужденная эластическая деформация уже не успевает за трещиной, размеры эластической зоны вначале «замораживаются», а с переходом к атермической стадии движения трещины эластическая зона исчезает, и заключительный этап разрушения происходит по хрупкому механизму-трещина «летит» адиабатически с высокой локальной температурой в ее головной части. Таким образом, условие  определяет отсутствие эластической зоны. Таковы результаты компьютерного моделирования.

           Итак, при температурах выше температуры хрупкости в нагруженном материале в окрестности трещины появляется эластическая зона, заполненная нелинейно деформированным полимерным веществом. Материал зоны подвергается вынужденной эластической деформации ползучести, связанной с большими макроскопическими перемещениями. Вне зоны материал образца испытывает только упругие деформации. На микроскопическом уровне развитие вынужденной эластической ползучести обусловленной  возникновением в силовом поле вынужденной сегментальной подвижности и проявляется в изменении конформаций макромолекул от свернутых к вытянутым без их разрыва и перемещения как целого. При этом изменяется (уменьшается) конформационная энтропия макромолекул. В этом смысле вынужденная эластическая деформация имеет энтропийное происхождение. Но конформационные преобразования при вынужденной ползучести происходят с преодолением блокирующего действия межмолекулярных сил, поэтому изменяется не только энтропия, но и внутренняя энергия макромолекул. Поэтому характер вынужденной эластической деформации не чисто энтропийный. Тормозящее действие межмолекулярных сил проявляется как внутреннее трение, на преодоление которого затрачивается работа, которая рассеивается в виде тепла. Поэтому при формировании эластической зоны она нагревается.

     Таким образом, в эластической зоне деформация имеет две составляющие – упругую, которая возникает практически мгновенно, и запаздывающую – вынужденноэластическую. Упругая составляющая обусловлена растяжением химических связей и валентных углов, в первую очередь, в цепях главной валентности полимерных макромолекул. Эластическая составляющая появляется только выше температуры хрупкости, т.к. только при этих температурах «размораживается» сегментальная подвижность. Она проявляется как вынужденная ползучесть в стесненных условиях малого объема эластической зоны. Ее развитие растянуто во времени, а по величине эластическая составляющая значительно превосходит упругую. Все это позволяет записать тензор деформаций в эластической зоне в виде

                                                    (10)

где q(T-Tхр)-функция Хевисайда. Он зависит от пространственных координат произвольной точки M зоны и от времени. Эта формула действует только в пределах эластической зоны, которая при понижении температуры до температуры хрупкости  стягивается к клюву трещины. При температурах ниже  эластическая зона отсутствует, и в этой формуле остается только первое слагаемое. Тензор вынужденной эластической деформации разложим обычным образом на шаровую и девиаторную части

                                                                        (11)                                                      

где - след тензора эластической деформации, а

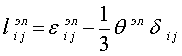                                                                                              (12)      

девиатор тензора эластической деформации.

Вынужденная эластическая деформация развивается в стесненных условиях малого объема окрестности трещины. За пределами эластической зоны материал деформируется только упруго. Поэтому при деформации эластической зоны изменение объема не происходит, и существенным является только девиатор деформации. В связи с этим уточним формулу (10)

                                                    (13)

В пределах эластической зоны (когда она есть) устанавливается напряжение, равное пределу вынужденной эластичности. Для нормальных и тангенциальных компонент напряжений предел вынужденной эластичности, вообще говоря, различен. Как правило, для сдвига он меньше, чем для растяжения [1]. Поэтому, например, для трещины поперечного сдвига размеры эластической зоны определяются значением предела вынужденной эластичности на сдвиг, и эластическая составляющая деформации появляется, когда тангенциальное напряжение достигает предела вынужденной эластичности для данной температуры.

В упругом тензоре деформаций   существенны и шаровая часть и девиатор, т.к. при упругой деформации изменяется и объем и форма. Деформация химических связей и валентных углов в макромолекулах – это всегда упругое растяжение, но оно вызывается всеми компонентами тензора напряжений, т.к. на микроскопическом уровне всегда имеются химические связи в макромолекулах, растягиваемые всеми компонентами макроскопического напряжения.

       В процессе формирования эластической зоны возникают вязкие или диссипативные напряжения, вызванные силами внутреннего трения. Вязкие напряжения зависят от скорости вынужденной эластической деформации и исчезают, когда развитие этой деформации завершается. Работа, производимая вязкими напряжениями, определяет потери энергии при деформировании. Эта энергия рассеивается в виде тепла, поэтому при формировании эластической зоны ее вещество нагревается. Потери энергии на трение в единице объема в единицу времени определяются т.н. диссипативной функцией , а именно выражение  определяет потери энергии в малом объеме  около точки М за малое время  около момента t. Мощность тепловыделения в единице объема  равна

                                                               (14)                                                                               

Количество тепла, которое выделяется во всем объеме эластической зоны V за промежуток времени [t1,t2] равно

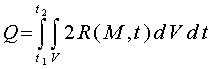                                                                                           (15)  

Диссипативная функция  является квадратичной функцией тензора скоростей эластической деформации . Тензор вынужденной эластической деформации представляется суммой девиатора и шаровой части, получаем

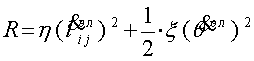
                                                 (16)                                                               

Здесь точкой обозначено дифференцирование по времени, а  и  - коэффициенты вязкости, именно - вязкость формы (на сдвиг), - вязкость объема. Поскольку в рассматриваемом случае вынужденная эластическая деформация определяется девиатором , то от этой формулы остается

                                                                                                       (17)         

Тогда мощность тепловыделения в произвольной точке М эластической зоны будет

                                                                            (18)  

Зависимость девиатора эластической деформации от времени определяется реологическими свойствами полимерного вещества. Для оценки этих свойств можно взять реологическую модель Кельвина (линейное стандартное тело). Эта модель сочетает в себе мгновенную упругость и запаздывающую упругость, обусловленную вязкостью материала. Мгновенная упругость характеризуется мгновенным модулем упругости Е, а запаздывающая – вязкостью  и временем запаздывания . В одномерном случае ползучесть материала Кельвина описывается формулой

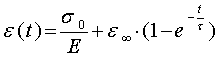                                                                         (19)      

Здесь - приложенное напряжения, а - равновесное значение запаздывающей деформации, равное

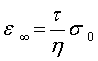                                                                                                        (20)      

Первое слагаемое в формуле (19) определяет мгновенную упругую деформацию и соответствует первому члену формулы (10 ), а второе – запаздывающую вынужденную эластическую деформацию, соответствующую второму члену формулы (10). Отталкиваясь от формулы (19), запишем девиатор вынужденной эластической деформации в виде

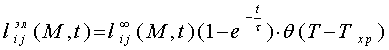                                          (21)      

Тогда скорость этой деформации будет

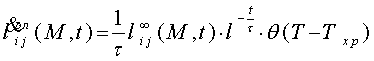                                (22)                                  

Подставим это в формулу (18) получаем мощность тепловыделения, равную

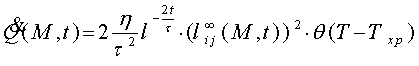                        (23)                                             

Это означает, что в процессе формирования эластической зоны в каждой точке ее объема действует тепловой источник с такой мощностью. Количество тепла, которое выделяется за  время формирования эластической зоны, получим, если подставить (23) в формулу (14)   и произвести предусмотренное там интегрирования

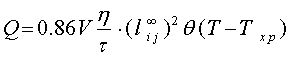                                             (24)                                  

Здесь V- объем эластической зоны, а - средняя равновесная эластическая деформация.

По завершении формирования эластической зоны в ней устанавливается однородное напряжение, равное пределу вынужденной эластичности. Тогда количество выделяющегося тепла в эластической зоне окончательно будет равно

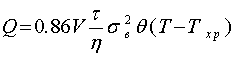                                                                  (25)

                                                         Литература

 

1.Бартенев Г.М.//Прочность и механизм  разрушения полимеров.М.:Химия.1984.-280с.

2. Валишин А.А., Карташов Э.М., Тишаева С.Д. // Учёные записки МИТХТ-2003.-№ 7.-С.40-45.

3. Баренблатт Г.И. В кн.:Проблемы механики сплошных сред.-Изд-во АН СССР.-М.-Л..-1961.

4. Баренблатт Г.И.//Прикладная математика и механика.-1964.-28,№4.-с.630-643.

5. Панасюк В.В. Предельное равновесие хрупких тел с трещинами. Киев.-Наукова Думка.-1968.

6. Ландау Л.Д., Лифшиц Е.М. Теория упругости.М.:Наука.-1978.-358с.

7. Керштейн И.М., Клюшников В.Д., Ломакин Е.В., Шестериков С.А. Основы экспериментальной механики разрушения. М.:Изд-во МГУ.-1989.с.61.

8. Костров Б.В. //Прикладная математика и механика.-1974.-38,№3.-с.551-560.

9. Партон В.З. Механика разрушения . –М.: Наука.-1990.-с.157.

10. Черепанов Г.П. Механика хрупкогот разрушения.М.:Наука,1974.-640с.

11. Fehlebeck D.K., Orowan E.O.// Weld. Journ. Ress. Suppl.-1955.-34.-p.570-575.