4 страниц

К.т.н., доцент Саакян С.А., Научный исследователь Дарахчян М.К.

Государственный Инженерный Университет Армении

ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ СВОБОДНОЙ ГРАНИЦЫ АРГУМЕНТА В ОДНОМЕРНЫХ ВАРИАЦИОННЫХ ЗАДАЧАХ УПРАВЛЕНИЯ

В оптимальных системах управления существование достаточных условий свободных границ (СГ) полностью не исследованы, в том числе и при простейшей задаче вариационного исчисления (ВИ). В них необходимые условия существования СГ описываются уравнениями Эйлера-Пуасона в общем уравнении вариации [1]. Выявление достаточных условий существования СГ на основе второй вариации, в связи с наличием неизвестных параметров, связаны с определенными трудностями. В настоящей статье исследуется достаточное условие существования правостороннего свободного параметра аргумента в задачах одномерного неавтономного ВИ, математическое описание которого имеет вид:

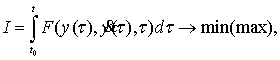(1)

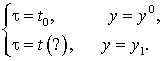(2)

Основываемся на том, что оптимальная функция зависит не только от текущего значения аргумента , но и от граничного параметра аргумента . При этом оптимальную функцию можно представить в виде

(3)

Оптимальное значение функционала (1) при этом также является функцией граничного параметра . В результате будем иметь следующую задачу экстремума:

(4)

Изменение оптимального значения функционала при отклонениях граничного значения аргумента определяем рядом Тейлора:

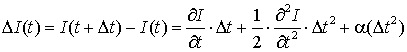, (5)

где - слагаемые членов высших порядков. Из выражения (5) следует достаточное условие существования СГ значения аргумента:

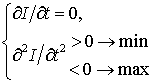(6)

В аналитически решаемых задачах можно найти коэффициенты в (5) и тем самим решить вопрос существования свободного граничного параметра аргумента. В тех случаях, когда задача решается только цифровыми методами, коэффициенты в (5) будут определены в результате разложения интегрального выражения (1) в ряд относительно граничного параметра аргумента при ее отклонениях.

Предполагается, что функции и имеют непрерывные частные производные высших порядков. Изменение оптимального значения функционала (1) можно определить следующим выражением:

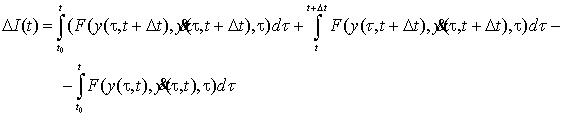(7)

Разлагая подинтегральное выражение в ряд Тейлора вторым приближением, будем иметь:

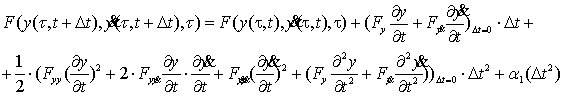(8)

где

Интегрируя по частям, с учетом выражения (8) в (7), и пользуясь граничными соотношениями частных производных функции [2], получим:

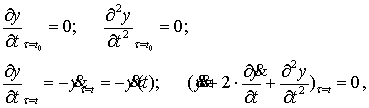(9)

где Учитывая также, что функция

_{удовлетворяет уравнению Эйлера, для оценки изменения функционала будем иметь}

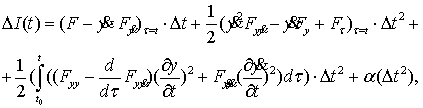(10)

откуда и определяются коэффициенты в ряде (5):

(11)

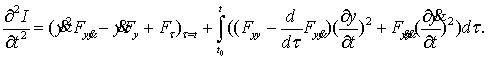(12)

Функции и являются решением задачи Для определения коэффициента необходимо иметь функции и . Эти функции можно определить, решая уравнение вариации первой степени относительно аргумента [3]

(13)

с учетом граничных условии (9).

Таким образом, для определения коэффициентов в ряде (5) необходимо дополнительно решить дифференциальное уравнение второго порядка (13) с граничными условиями (9).

В тех случиях, когда коэффициенты в (11) и (12) имеют нулевые значения

необходимо в рядах (5) или (10) определить первый нулевой коэффициент высшего порядка, и тем самым решить вопрос существования свободного граничного параметра аргумента [4] или необходимо дополнительно два раза (при положительном и отрицательном ) решить задачу и сравнить оптимальные значения функционала.

Литература

1. Петров Ю.П. Вариационные методы теории оптимального управления.-2-е изд. Перераб. и доп. –Л.: Энергия, 1977.-220с.

2. Саакян С.А. Оценка изменения показателей эффективности в динамических системах управления // Вестник Инженерной Академии Армении. – Ереван, 2005.-Т.2, N1. – С. 131-134.

3. Саакян С.А. Дарахчян М.К. Определение частных производных оптимальной функции по граничным параметрам в вариационных задачах управления // Вестник ГИУА.-Ереван, 2009.- Том 1, N1. –с. 514-517.

4. Дегтярев Ю.И. Методы оптимизации. Уч. Пособие для вузов. –М: Сов. Радио, 1980-272с.