К. т. н., Бондаренко Л.Н., Бондарева О.А., Середа О.В.

Днепропетровский национальный университет железнодорожного транспорта

имени академика В. Лазаряна

ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ КАЧЕНИЮ

КОЛЕСА ОТ КРУГЛОСТИ

Колеса механизмов передвижения кранов, тележек и другие детали машин всегда имеют то или иное отклонение от круглости, обусловленное как технологией изготовления, так и появляющуюся в результате износа.

Характерной особенностью такой детали является то, что при качении она имеет переменный во времени радиус кривизны в месте контакта.

Предположим, что катящееся колесо имеет форму эллипса (рис. 1) с коэффициентом сжатия , где a – большая ось; b – малая ось.

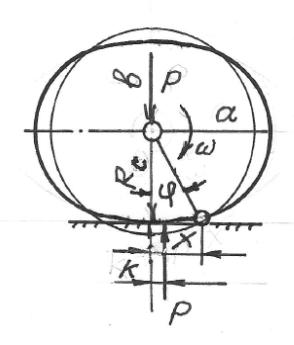
Рис. 1 Расчетная схема для определения сопротивления качению колеса эллипсовидной формы.

Пусть в начальный период времени большая ось колеса расположена параллельно горизонту. Контакт в этом случае происходит в вершине с наибольшим радиусом кривизны, величина которого определяется из аналитической геометрии:

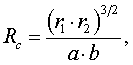(1)

где - эксцентриситет; - абсцисса точки на линии эллипса, измеряемая от точки пересечения осей. Ввиду двойной симметрии эллипса можно рассмотреть значения в интервале

Для определения соотношения между абсциссой и углом поворота эллипса учтем то обстоятельство, что длины эллипса с достаточной для практических расчетов точностью может быть найдена из соотношения:

(2)

Здесь выражение в скобках представляет собой два члена ряда разложения полного эллиптического интеграла 2-го рода при помощи которого вычисляется длина эллипса.

Равновеликой длине L будет длины окружности с радиусом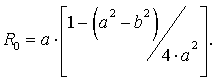

Теперь соотношение между поворотом эллипса на угол и абсциссой запишется в виде:

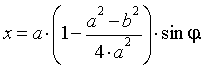(3)

Из курса аналитической геометрии радиус кривизны эллипса в любой точке:

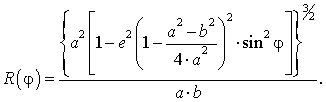(4)

При известных величинах и нагрузке на колесо может быть найдена полуширина пятна контакта и коэффициент трения качения в функции угла поворота колеса.

Полуширина пятна контакта при схеме касания «цилиндр-плоскость», равенстве модулей упругости цилиндра и плоскости и равенстве коэффициента Пуассона 0,3

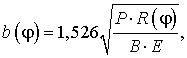(5)

где - длина цилиндра.

Коэффициент трения качения

(6)

где - в метрах.

Зависимость от угла поворота колеса сопротивления передвижению при показаны на рис.2.

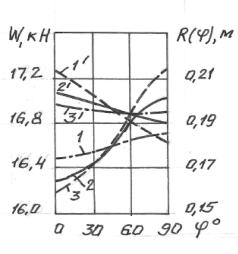
Рис.2 Зависимости от угла поворота колеса : 1, 2, 3 – сопротивления передвижению при коэффициентах сжатия 0,99; 0,97 и 0,95 соответственно; 1', 2', 3' – радиусы кривизны колеса в месте контакта.

Анализ графиков на рис.2 показывает, что при реальной величине коэффициента сжатия сопротивление качению колеса отличается более чем на 7% при и , что должно учитываться при расчете деталей механизмов передвижения.

Литература:

1. Справочник по сопротивлению материалов /Писаренко Г.С., Яковлев А.П., Матвеев В.В. – К.: Наук. думка, 1988. – 736 с.

2. Бондаренко Л.М. Аналітично-експериментальне визначення коефіцієнта тертя кочення /Будівництво України, 2001. – с. 47-48