Технические науки/Механика

К.т.н., доцент И. А. Трегубова

Одесская национальная академия связи им. А.С. Попова

Рациональное использование анизотропных свойств материала при формировании поверхности оболочки

Проектирование оболочек-покрытий состоит из нескольких этапов, первым из которых является этап эскизного проектирования.

На этом этапе, с доступной для него погрешностью, ведется поиск геометрической формы поверхности с учетом различных требований. К одним из них относится учет особенностей свойств материала и умелое использование прочностных и деформационных возможностей в различных направлениях при формировании поверхности.

Так как анизотропные материалы обладают различными механическими свойствами в разных направлениях, то учет последних является одним из основных требований при поиске геометрической формы оболочки. Анизотропия обусловлена структурой, строением и составом материала. Так, к примеру, в направлении вдоль волокон такой материал может обладать наибольшими прочностными и упругими свойствами, а в направлении поперек волокон – наименьшими, что подтверждается соответствующими модулями упругости. Показатели упругости при растяжении, сжатии и изгибе поперек волокон значительно ниже, чем вдоль волокон.

Вследствие высокого модуля упругости вдоль волокон анизотропный материал эффективно располагать в оболочках в том направлении, где бы максимально использовались высокие прочностные и деформационные свойства материала. В тоже время, низкий модуль упругости поперек волокон позволяет использовать этот материал в тех направлениях, где невелико влияние его деформативности. Таким образом, правильное использование физико-механических свойств анизотропных материалов при формировании поверхности ведет к определению ее рациональной формы и требует решения комплекса геометрических задач на этапе эскизного проектирования оболочек. На этом этапе встречаются задачи, где необходимо построить дискретный обвод, проходящий через наперед заданные точки, если известно, что прочностные и деформативные свойства материала в двух взаимно перпендикулярных направлениях отличаются весовым коэффициентом К учета свойств упругости материала.

Для решения поставленной задачи воспользуемся известным в литературе способом формирования оболочек, позволяющим управлять ее формой с учетом напряжений, возникающих в ней, и основанный на конечно-разностной аппроксимации дифференциальных уравнений [1].

Рассматриваемая поверхность заменяется дискретной упруго-изогнутой сетью. Совокупность узлов и связей сети, между которыми устанавливается функциональная зависимость в виде конечно-разностного уравнения, называется звездой сети. В основу получения такого конечно-разностного уравнения положена физическая модель дискретной упругой рейки [2].

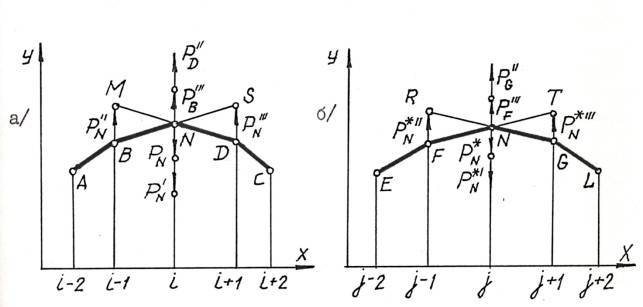
Рис. 1

Дискретная геометрическая модель гибкой рейки может быть представлена в виде ломаной линии с шарнирным закреплением в узлах (рис.1), на звеньях которой действуют изгибающие моменты, стремящиеся выпрямить каждую пару соседних звеньев.

Узлы ломаной, совпадающие с наперед заданными точками, через которые необходимо провести дискретный обвод, назовем закрепленными, остальные узлы будут считаться незакрепленными. Если каждому незакрепленному узлу ломаной со звеньями переменной длины предоставить возможность свободного перемещения в плоскости ломаной, то под действием изгибающих моментов они будут перемещаться до тех пор, пока система не уравновесится. Положение незакрепленных узлов на плоскости определяется системой уравнений равновесия. Для получения уравнения равновесия любого незакрепленного узла необходимо изгибающие моменты разложить на эквивалентные им пары сил, векторная сумма которых должна быть равна нулю.

Обобщение дискретного представления упругой рейки позволяет построить модель упругой сети. Представляя дискретный сетчатый каркас поверхности в виде множества гибких реек, ориентированных по двум направлениям, можно построить сеть с четырехугольной ячейкой, проходящую через наперед заданные узловые точки. Планом такой сети является правильная квадратная сетка. Этот принцип позволяет перейти от плоского дискретного обвода к двумерному путем сложения сил, действующих на узлы ломаных различных направлений и получить конечно-разностное уравнение равновесия узла, являющегося общим для двух семейств ломаных, которое имеет вид

(1)

где - соответствующие порядковые номера узлов сети.

Уравнение равновесия (1) и соответствующий ему вычислительный шаблон (рис.2), составляются для незакрепленных узлов дискретных сетей, выполненных из изотропных материалов. При этом условии весовой коэффициент К учета свойств упругости во всех направлениях равен единице (K=1). Если оболочка выполнена из анизотропного материала, то вид уравнения равновесия (1) изменится, так как в него необходимо будет ввести весовой коэффициент К учета упругих свойств материала.

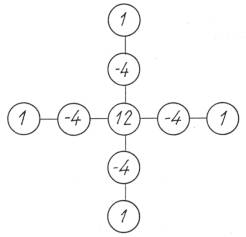
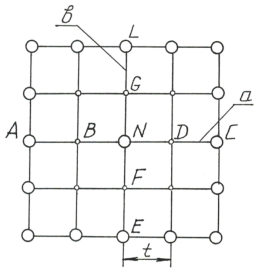
Рис.2 Рис.3

Пусть в оболочке, выполненной из анизотропного материала, закрепленными узлами сети (рис.3) являются узлы квадратного опорного контура и центральный узел N . Известно, что деформационные и прочностные возможности материала в двух взаимно-перпендикулярных направлениях отличаются весовым коэффициентом К. В направлении ломаной а=ABNDC коэффициент К=1, а в направлении ломаной b=EFNGL K=k. Таким образом, усилия, действующие вдоль ломаной b в К раз отличаются от усилий в ломаной a. Узел N лежит на пересечении этих двух ломаных а и b.

Для получения уравнения равновесия произвольного незакрепленного узла N необходимо определить величину изгибающих моментов, возникающих в узлах ломаной a и в узлах ломаной b. Изгибающие моменты заменим эквивалентными им парами вертикальных усилий ( рис. 1). Плечом каждого момента будет разность абсцисс смежных узлов, которую для всех звеньев примем одинаковой и равной заданному шагу t. Величину изгибающего момента в узле N, лежащего на ломаной a, примем равной

(2)

Выражая ординаты узлов точек М и S в (2) через координаты узлов B, N, D получим

.

Аналогично определим изгибающие моменты в узлах B и D:

,

.

Запишем выражения для изгибающих моментов в узле N, лежащем на ломаной b. Так как усилия, действующие в узлах ломаной b, отличаются коэффициентом К от усилий, действующих в узлах ломаной а , то

,

,

.

Таким образом, получены выражения для определения изгибающих моментов в узлах дискретной сети, которой заменена поверхность оболочки, выполненная из анизотропного материала.

Литература:

1. Ковалев С.Н., Ахмедов Ю.Х. Линеаризация условий пластичности оболочек с помощью дискретных гиперсетей // Прикладная геометрия и инженерная графика. – К.: Будівельник, 1986. – Вып. 41. – С. 19-22 .

2. Михайленко В.Е., Ковалев С.Н., Сазонов К.А. Формирование большепролетных покрытий в архитектуре . – К: Вища школа. Головное изд., 1987. – 191 с.