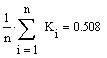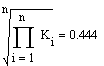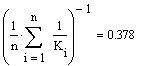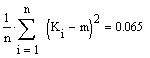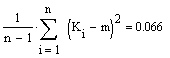Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

УДК 681.518.68:622.24

Семенцов Г.Н., Пархуць Х.В., Чигур Л.Я.

Івано-Франківський національний технічний університет нафти і газу

СТАТИСТИЧНІ ВЛАСТИВОСТІ ФЛУКТУАЦІЙ КОЕФІЦІЄНТУ МЕХАНІЧНОЇ ЕФЕКТИВНОСТІ ДОЛОТА

Автоматизація процесу керування відпрацюванням бурових доліт трактується [1,2] як одна із підзадач системи керування процесом буріння, головною задачею якої є виявлення початку завершального періоду роботи долота і прийняття рішення стосовно моменту підйому його для заміни.

Проте, процес буріння як об’єкт керування є нелінійним нестаціонарним невідтворюваним багатофакторним динамічним об’єктом, що функціонує за умов апріорної та поточної невизначеності щодо структури та параметрів, розвивається в часі і перебуває під впливом зовнішніх завад. Наявність таких специфічних ознак дає підстави говорити про специфічну методологію його дослідження, оскільки все це викликає погану організацію внутрішньої структури системи в розумінні нечіткого проявлення причинно-наслідкових відношень [2].

Разом з тим, процес буріння як об’єкт керування повинен бути формалізований у вигляді багатовимірної системи однонаправленого перетворення вхідних керувальних координат (осьової сили на долото , швидкості його обертання , витрати промивальної рідини ), а також вхідних контрольованих і неконтрольованих збурень (міцність, твердість, абразивність, буримість, пластичність та ін. гірських порід; пластові тиски, тертя колони бурильних труб в свердловині) у реакції об’єкта керування (проходка долота , показники, що характеризують технічний стан озброєння долота).

Тому завданням формалізації процесу буріння є встановлення в математичній формі причинно-наслідкових зв’язків змінних стану з вхідними величинами та .

Оскільки на процес буріння свердловини впливають численні фактори, які носять випадковий характер і які неможливо контролювати, то для отримання змістовних результатів, які б об’єктивно відтворювали основні закономірності завершального періоду роботи долота, зробимо такі припущення:

· буріння ведеться полікристалічними безопорними долотами нового покоління типу PDC;

· вся глибина свердловини розбита на певні інтервали, всередині яких міцність порід можна вважати постійною;

· протягом рейсу долота витрата промивальної рідини постійна і є такою, що забезпечує повне очищення вибою свердловини від шламу;

· керувальні впливи – осьова сила на долото та швидкість його обертання – взаємно незалежні параметри;

· на керувальні дії накладені технологічні обмеження

Для вирішення задачі автоматизації процесу керування відпрацюванням безопорних бурових доліт типу PDC математичну модель процесу буріння необхідно отримати у просторі станів. Для цього потрібна поточна інформація про проходку долота та про стан його озброєння.

Проте стан озброєння долота є невимірюваним показником і тому в математичній моделі його не повинно бути. Тому для оцінювання технічного стану озброєння шарошкових доліт користуються [2] узагальненою оцінкою стану озброєння доліт — функцією зносу , де – початкова швидкість буріння і поточне її значення. В зарубіжній практиці для оцінювання технічного стану доліт нового покоління користуються таким показником як механічна ефективність долота.

З існуючих наукових досліджень [1,2,4 та ін.] відомо, що структура функції зносу досліджувалась головним чином для традиційних з фрезерованими і твердосплавними зубцями шарошкових доліт. Зважаючи на це, технічний стан озброєння полікристалічних доліт PDC оцінюватимемо опосередковано через показник механічної ефективності долота , що являє собою відношення зміни механічної швидкості буріння в часі до початкової швидкості буріння : . Для полікристалічних доліт типу PDC цю залежність досліджуватимемо аналітично і експериментально на базі кореляційно-спектрального аналізу, об’єктом якого є сукупність показників процесу буріння, виміряні в дискретні моменти часу, які характеризують протягом рейсу долота його технічний стан [1, 2]. Вказані показники розуміються як реалізації випадкових процесів, властивості яких відомі частково або невідомі зовсім, але задані лише деякі їх обмеження.

Для розв’язку поставленої задачі аналізу експериментальних значень механічної ефективності долота (табл. 1) залучатимемо методи математичної статистики.

Таблиця 1 – Масив експериментальних значень механічної ефективності долота ЗУ 295 СЗГ (Свердловина № 814 Прикарпатського УБР, електробур Е240-8, інтервал буріння 2080,0-2089)

№		№		№		№
0	0.236	30	0.515	60	0.415	90	0.340
1	0.126	31	0.622	61	0.323	91	0.600
2	0.154	32	0.780	62	0.480	92	0.280
3	0.101	33	0.631	63	0.640	93	0.220
4	0.128	34	0.690	64	0.614	94	0.280
5	0.316	35	0.900	65	0.600	95	0.510
6	0.278	36	0.470	66	0.480	96	0.200
7	0.256	37	0.480	67	0.632	97	0.260
8	0.280	38	0.580	68	0.430	98	0.280
9	0.385	39	0.452	69	0.390	99	0.220
10	0.352	40	0.290	70	0.520	100	0.370
11	0.225	41	0.140	71	0.390	101	0.320
12	0.514	42	0.128	72	0.520	102	0.580
13	0.509	43	0.175	73	0.520	103	0.400
14	0.435	44	0.160	74	0.250	104	0.180
15	0.424	45	0.180	75	0.620	105	0.320
16	0.406	46	0.430	76	0.580	106	0.470
17	0.372	47	0.680	77	0.440	107	0.500
18	0.191	48	0.697	78	0.490	108	0.630
19	0.348	49	0.942	79	0.941	109	0.680
20	0.628	50	1.136	80	0.820	110	0.930
21	0.865	51	1.420	81	0.580	111	0.810
22	0.826	52	0.642	82	0.740	112	1.311
23	0.642	53	0.580	83	1.010	113	1.311
24	0.805	54	0.640	84	0.320	114	0.230
25	0.578	55	0.430	85	0.652	115	0.180
26	0.605	56	0.481	86	0.410	116	0.831
27	0.324	57	0.382	87	0.480	117	0.778
28	0.410	58	0.515	88	0.620	118	0.813
29	0.542	59	0.641	89	0.640

Визначимо математичне сподівання, дисперсію та середньоквадратичне відхилення за допомогою середовища Mathcad, для чого замінимо позначення на К.

Характеристики вибірки даних: ORIGIN := 1.

Cереднє арифметичне

Середнє геометричне

Середнє гармонічне

Дисперсія

Зміщена оцінка

Не зміщена оцінка

Середнє квадратичне відхилення

Зміщена оцінка

Не зміщена оцінка

Медіана

Мода

Ексцес

Асиметрія

У результаті отримали такі характеристики досліджуваного випадкового процесу, як оцінку математичного сподівання, дисперсію та середньоквадратичне відхилення. Оцінка математичного сподівання випадкового процесу в загальному вигляді являє собою деяку середню криву, навколо якої розподіляються всі можливі окремі реалізації даного процесу. Дисперсія var(K) і середньоквадратичне відхилення stdev(K) характеризують розсіювання окремих можливих реалізацій навколо цієї середньої кривої. Ці характеристики для кожного конкретного моменту є середніми з множини. Вони визначаються одномірним законом розподілу, який треба визначити.

Впорядкуємо досліджувану вибірку у порядку зростання:

n=118

Отримуємо таблицю значень:

	₀
₀	_0.101
₁	₀_.126
₂	_0.128
₃	_0.128
₄	_0.14
₅	_0.154
₆	_0.16
₇	_0.175
₈	_0.18
₉	_0.18
₁₀	_0.18
₁₁	_0.191
₁₂	_0.2
₁₃	_0.22
₁₄	_0.22
₁₅	_...

_Z₌

За допомогою формули Стерджеса визначаємо крок і довжину інтервалу, для чого визначимо зону розсіювання значень за формулою:

R:=max(К) – min(К)

R = 1.319

Розділимо вибірку на 8 груп із інтервалами h=0.203. Далі визначимо границі інтервалів та зберігаємо їх як масив int. Визначаємо середини інтервалів (масив x_i).

i := 0..7 int₀ := z₀ int_i₊₁:= int_i+h

Розраховуємо середини інтервалів, абсолютні частоти інтервалів та відносні частоти інтервалів. У результаті розрахунків отримуємо наступні значення:

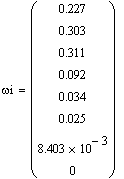
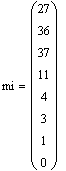
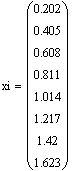
Виконуємо перевірку обчислення абсолютних та відносних частот:

За отриманими даними побудована гістограма густини відносних частот та закон розподілу (рис.1):

і := 1..8, n := 119

Для перевірки даної гіпотези скористались критерієм Пірсона :

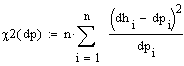(1)

0,311

0,303

0,225

0,0

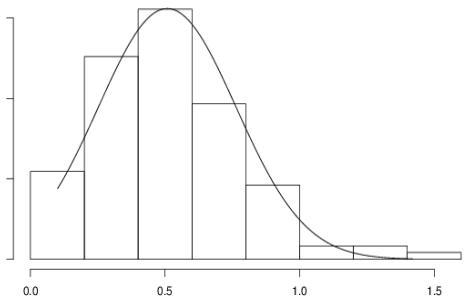
Рисунок 1 – Гістограма і нормальний закон розподілу для механічної ефективності долота К

По отриманим графікам можна припустити, що даний розподіл підпорядковується нормальному закону розподілу.

Для випадкової функції одномірний розподіл імовірності і отримані на основі нього характеристики, ще не є достатніми для оцінки характеру протікання випадкового процесу К(t) в часі. Необхідно ще встановити зв’язок між значеннями випадкового процесу в різні моменти часу.

Інтенсивність зміни випадкового сигналу в часі можна охарактеризувати за допомогою однієї з функцій – автокореляційної функції або функції спектральної густини. Автокореляційну функцію визначають за формулою [3,4]:

(2)

де τ – кореляційний зсув (лаг).

Оскільки досліджувана реалізація являє собою сукупність дискретних значень сигналу К(t), отриманих через рівні проміжки , то інтеграл (2) наближено замінимо сумою

(3)

де – центровані значення.

Для визначення нормованої автокореляційної функції скористались пакетом Matlab. Отримана оцінка нормованої автокореляційної функції наведена на рис.2.

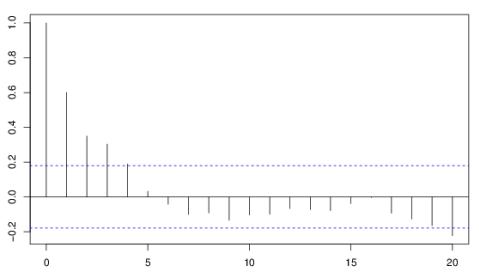
Рисунок 2 – Графічне зображення нормованої автокореляційної функції для механічної ефективності долота К

Рівняння, яким описується ця залежність, отримане за допомогою програми Curve Expert (рис.3).

Отже, рівняння автокореляційної функції має вигляд експоненціально-косинусної функції:

. (4)

З такими параметри: a=0,303; b=0,288.

Тоді рівняння (4) матиме вигляд:

При статистичному аналізі стаціонарних випадкових функцій зручно користуватись також спектральною густиною випадкової функції, тобто двохстороннім зображенням Фур’є автокореляційної функції [4]

, (5)

де R_КК(t) – оригінал автокореляційної функції механічної ефективності долота.

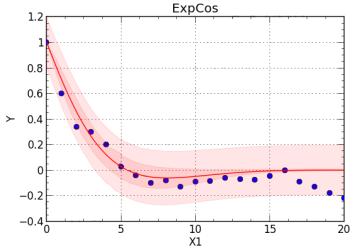
Рисунок 3 – Рівняння і графічне зображення нормованої автокореляційної функції для механічної ефективності долота К при використанні Curve Expert

Спектральна густина є додатною функцією у всьому діапазоні частот від 0 до ¥. Вона не містить відомостей про фази окремих гармонійних складових. За допомогою приведеної формули можна визначити спектральну густину по заданій аналітично автокореляційній функції R_КК(t).

Визначимо спектральну густину , використовуючи пакет MathCad, для чого збережемо отримані значення функції в масив даних:

(6)

Далі використаємо перетворення Фур’є, взявши за основу вбудовану функцію

(7)

Отримане перетворення потрібно взяти по модулю, оскільки спектральна густина є додатною у всьому діапазоні частот. Отже

(8)

(9)

(10)

По отриманих даних побудуємо графік спектральної густини . Модуль значення спектральної густини визначає амплітудно-частотну характеристику (АЧХ) сигналу, а її аргумент є фазочастотною характеристикою (ФЧХ). АЧХ сигналу являється парною функцією, а ФЧХ – непарною. В загальному вигляді зміст визначається як амплітуда сигналу, що припадає на 1 Гц в нескінченно вузькій полосі частот, яка включає в себе розглянуту частоту w.

Отже, кореляційній функції (4) відповідає спектральна густина

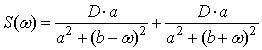. (11)

Підставивши коефіцієнти, отримали таку функцію спектральної густини:

. (12)

Графік спектральної густини для механічної ефективності долота наведено на рис.4.

При дослідженні автоматичних систем виникає необхідність створювати типові випадкові впливи штучно – за допомогою спеціальних генераторів. Найпростіше ця задача вирішується з використанням методу формуючого фільтра. Суть методу полягає в тому, що потрібний випадковий сигнал отримується шляхом пропускання білого шуму через фільтр з відповідною частотною характеристикою.

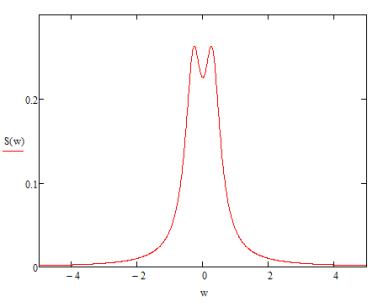
Рисунок 4 – Графік спектральної густини для механічної ефективності долота К

Частотна передавальна функція W_ф(jω) фільтра зв’язана з спектральною густиною S(w) формуючого сигналу наступним співвідношенням [3]:

{W_ф(jω)}²= S(w). (13)

Для пошуку функції W_ф(jω) необхідно розкласти спектральну густину S(w) на спряжені множники W_ф(jω) і W_ф(-jω). З цих двох множників фізично реалізованим у вигляді фільтра є лише перший множник.

Для сигналу з експоненціально-косинусною кореляційною функцією маємо [3]:

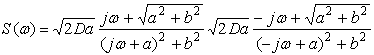. (14)

Звідси частотна функція фізично реалізованого фільтра:

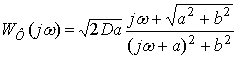. (15)

Тоді, для маємо:

Виділимо дійсну і уявну складові, здійснивши ряд перетворень:

;

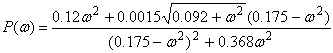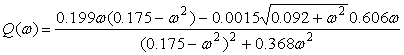Виводимо графік для АФХ формуючого фільтру за допомогою програми Mathcad.

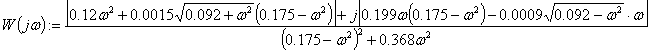
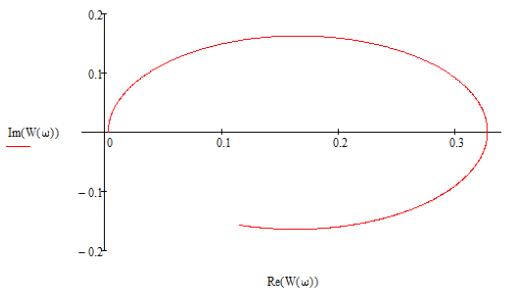
Рисунок 5 – Графік АФХ формуючого фільтру для механічної ефективності долота К

Висновок

Доведено, що досліджуваний процес зміни в часі коефіцієнта механічної ефективності долота є стаціонарним і ергодичним, має нормальний закон розподілу. Для досягнення якісних показів вимірювальних приладів визначено передавальну функцію формуючого фільтру.

Література

1. Драганчук О.Т. Аналіз відпрацювання доліт РДС на родовищах Ураїни і світу / О.Т.Драганчук, Т.О.Пригоровська // Нафтогазова енергетика. – 2008, №4. – С. 11-15.

2. Горбійчук М.І. Оптимізація процесу буріння глибоких свердловин: [навчальний посібник] / М.І.Горбійчук, Г.Н. Семенцов. – Івано-Франківськ: ІФНТУНГ, 2003. – 493 с.

3. Семенцов Г.Н. Теорія автоматичного керування: [навчальний посібник] / Г.Н. Семенцов. – Івано-Франківськ: ІФНТУНГ, 1999. – 611 с.

4. Семенцов Г.Н. Аналіз ергодичності випадкових процесів в системах керування / Г.Н.Семенцов, О.В.Фадєєва // Вісник Хмельницького національного університету. Технічні науки. - 2008. - №1. – С.74-80.