Технические науки/6. Электротехника и радиоэлектроника

Ст. преп. Балгабекова Л. О.

Алматинский университет энергетики и связи

ИССЛЕДОВАНИЕ ПЛОТНОСТИ ПОСТУПЛЕНИЯ ПАКЕТОВ ИЗМЕРЕННОГО ВИДЕО ТРАФИКА MPEG И АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ

С целью изучения основных статистических свойств измеренного видео трафика MPEG был проведен анализ экспериментальных данных.

На рисунке 1 представлен временной ряд (time series) – последовательность упорядоченных во времени зависимости числа пакетов в единицу времени.

Совокупность Xn таких измерений называют выборкой случайной величины X, сами измерения называют элементами выборки, а число измерений n – объемом выборки. Временной ряд включает два элемента время и количество пакетов (уровень ряда).

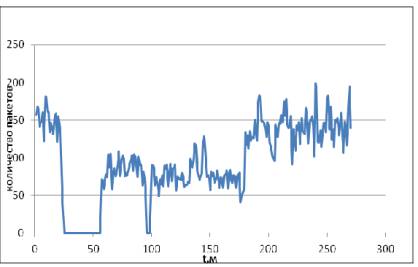
Рисунок 1 – Число пакетов в единицу времени (м)

Числовые характеристики общего измеренного трафика данных представлены в таблице 1.

Таблица 1 – Числовые характеристики случайной величины

Наименование	Значение
Математическое ожидание	0,014428395
Дисперсия	0,00045443
Среднеквадратическое отклонение	0,021317
Коэффициент вариации	1,47

Выше представленный временной ряд зависимости числа пакетов в единицу времени проверим на наличие корреляционной зависимости. Это корреляция, проявляющаяся во времени. Корреляционная зависимость между последовательными уровнями временного ряда называется автокорреляцией уровней ряда. Автокорреляция – корреляция ряда с самим собой, с задержкой на k наблюдений (k обычно называют лагом). Лаг – показатель, отражающий отставание или опережение во времени одного явления по сравнению с другим, связанным с ним. Коэффициент корреляции является мерой линейной зависимости между наблюдениями, разделенными определенными временными интервалами – мерой линейной связи между смежными наблюдениями. Совокупность коэффициентов автокорреляции, основанных на разной величине лага, есть не что иное, как расчетная автокорреляционная функция, график которой обычно называют коррелограммой. Коррелограмма показывает численно и графически автокорреляционную функцию (AКФ). Коррелограмма позволяет исследовать структуру временного ряда, выявлять наличие его компонент. Последовательность коэффициентов автокорреляции уровней первого, второго и других порядков называется автокорреляционной функцией временного ряда. Анализ автокорреляционной функции и коррелограммы позволяет найти лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями временного ряда наиболее тесная.

Определим обладает ли временной ряд медленно убывающей зависимостью или быстро убывающей зависимостью. Процесс Х обладает МУЗ, если для его АКФ выполняется условие

(1)

где ;

L_l – медленно меняющаяся на бесконечности функция

для всех Х.

Процессы с МУЗ характеризуются автокорреляционной функцией, которая убывает по степенному закону при увеличении временной задержки (лага). В отличие от процессов с МУЗ, процессы с БУЗ обладают экспоненциально спадающей АКФ вида

(2)

Вычисление АКФ выполнено с помощью программы Microsoft Office Excel по формуле (рисунок 2) результаты вычислений:

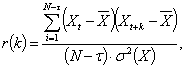(3)

где - выборочное среднее ряда Х;

- выборочная дисперсия ряда Х;

k=0, 1, 2,…

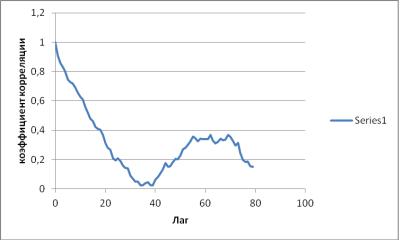
Рисунок 2 – Коррелограмма

Вид выборочной автокорреляционной функции тесно связан со структурой ряда:

- для стационарного ряда АКФ быстро убывает с ростом k;

- в нашем примере автокорреляционная функция приобретает характерный вид очень медленно спадающей кривой было рассчитано при лаге равном 69 из имеющихся 270 значений т. есть АКФ имеет отчетливый тренд (одно из свойств самоподобия). Они не обращаются в ноль при больших значениях k, что говорит о медленном убывании АКФ (гиперболически по степенному закону) при увеличении лага и о том, присутствует МУЗ.

Литература:

1. Шелухин О.И., Осин А.В., Смольский С. М. Самоподобие и фракталы. - М.: ФИЗМАТЛИТ, 2008.- 214 с.