Жолдыбаев М.Е.

Актюбинский региональный государственный

университет им. К.Жубанова, Казахстан.

Асимптотическое решение краевой задачи с начальным скачком для линейного сингулярно возмущенного интегро-дифференциального уравнения в частных производных второго порядка

1. Постановка задачи

Рассмотрим в области линейное сингулярно возмущенное интегро-дифференциальное уравнение в частных производных второго порядка вида:

(1)

,

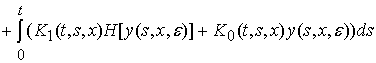удовлетворяющее краевым условиям:

, . (2)

Здесь - малый параметр, - независимые переменные, - искомая функция, , и функции заданные в области , а операторы:

,

где функция также задана в области .

Предположим, что:

1) функции ,, и - достаточно гладкие по совокупности аргументов ;

2) , , ,

где , - некоторые вещественные числа;

3) функции и являются решениями уравнения характеристики:

,

соответствующего уравнению (1), и удовлетворяющее начальным условиям

4) для функции

,

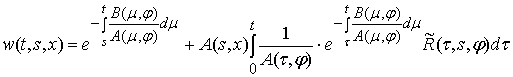значение удовлетворяет условию

, (3)

где резольвента ядра :

.

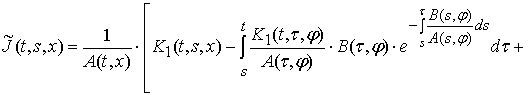
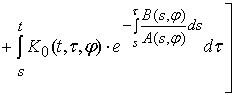Цель работы: построить равномерное в области асимптотическое разложение по малому параметру для решения сингулярно возмущенной задачи (1), (2).

2. Построение асимптотического разложения

Для построения асимптотики решения краевой задачи (1), (2) рассмотрим вспомагательную задачу Коши с начальным скачком, т.е.

(4)

где - неизвестная функция, представимая в виде:

. (5)

Решения возмущенной задачи (1), (4) ищется в виде:

, (6)

где - погранслойная независимая переменная, - регулярная часть асимптотики решения задачи (1), (4) определяемое асимптотическим рядом по малому параметру :

(7)

а - погранслойная часть:

. (8)

Коэффициенты разложения (7) и разложения (8) последовательно определяются из следующих задач:

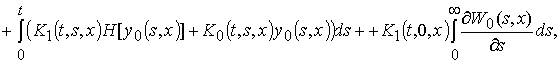
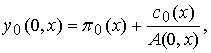(9)

, .

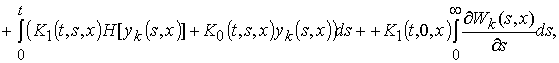
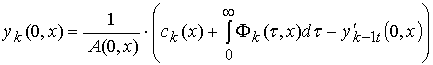
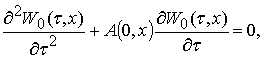
(10)

, .

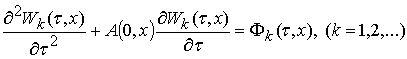
где -известная функция, которая выражается через функции , легко доказывается сходимость несобственных интегралов в (9).

Так как по условию 4) значение (3), то из (9) и полагая

, ,

неизвестные функций , входящие в (5), определяется из следующих уравнений:

,

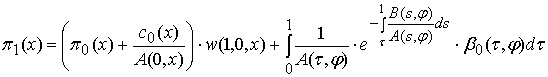
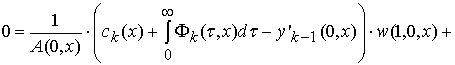
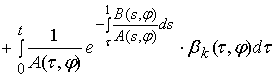где .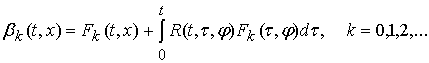

Для функций (7), (8) справедлива

Лемма. Пусть выполнены условия 1)-4). Тогда в области решение задачи (9) и решение задачи (10) , существуют, единственны и для них справедливы следующие оценки:

где - некоторое действительное число.

3. Оценка остаточного члена

Из разложений (7), (8) с уетом с учетом суммы (6) образуем частичную сумму вида [2]:

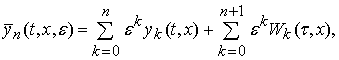
, (11)

где коэффициенты , однозначно определяются из задач (9), (10).

Можно доказать, что функция выражаемая формулой (11), в области является приближенным решением сингулярно возмущенной задачи (1), (2) с точностью порядка , т.е.:

.

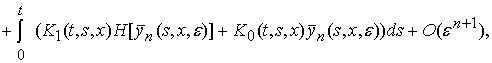
Обозначим через разность между точным решением возмущенной задачи (1), (2) и ее приближенным решением . Тогда будем иметь:

Справедлива следующая теорема, которая в силу громоздкости приводится без доказательства.

Теорема. Если справедливы условия 1)-4), то в некоторой достаточно малой окрестности значения существует единственное значение , представимое в виде , такое что решение сингулярно возмущенной задачи (1), (4) в области является единственным решением сингулярно возмущенной краевой задачи (1), (10) и это решение допускает следующее асимптотическое разложение:

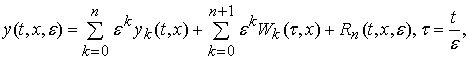
коэффициенты и однозначно определяются соответственно из задач (8) и (9), а остаточный член удовлетворяет оценкам

где - некоторая постоянная, независящая от и .

Литература

1. Ломов С.А. Введение в общую теорию сингулярных возмущений. М.Наука, 1981, 400 с.

2. Касымов К.А. Линейные сингулярно возмущенные дифференциальные уравнения второго порядка. Алма-ата, 1981.

3. Тажимуратов И.Т., Жолдыбаев М.Е., Оценки решений сингулярно-возмущенных уравнений в частных производных второго порядка. // Известия НАН РК. 2000, № 3, с. 56-62.