Таттибеков
К.С.
Таразский
государственный педагогический институт, Казахстан
Солитоны в одной
магнитоупругой модели
В настоящее время понятие солитона получило широкое
распространение. Это объясняется его универсальностью и обилием приложений при
выяснении различных процессов в нелинейных средах. Математический аппарат
теории солитонов - метод обратной задачи рассеяния - стал мощным инструментом
для исследования нелинейных уравнений в частных производных. МОЗР позволяет
построить точные N - солитонные решения
интегрируемых эволюционных уравнений, когда для них известны соответствующие
задачи рассеяния. Если последние неизвестны, то N - солитонные решения
интегрируемых уравнений могут быть найдены прямыми методами - метод
преобразования Бэклунда, метод Хироты. Более того, метод Хироты [1,2] дает
возможность получить солитонные решения и неинтегрируемых уравнений в частных
производных.
Рассмотрим систему нелинейных эволюционных уравнений,
описывающую магнитоупругую динамику в ферромагнетиках [3]:
![]() (1a)
(1a)
![]() (1б)
(1б)
![]() (1в)
(1в)
с граничными условиями на бесконечности
![]() ,
(2)
,
(2)
где ![]() ,
, ![]() - посстоянные действительные числа.
- посстоянные действительные числа.
Далее,
используя условие
![]()
уменьшим
число неизвестных функции на одну. Для этого достаточно перейти к новой
неизвестной функции ![]() по формулам
по формулам
![]() ,
, ![]()
где
* - означает комплексное сопряжение. Тогда система (1) и граничные условия (2) переходят
соответственно к
![]() , (3a)
, (3a)
![]() (3б)
(3б)
![]() (4)
(4)
Система нелинейных дифференциальных уравнений (3) инвариантна
относительно группы сдвигов в пространстве независимых переменных
![]()
![]() - действительный параметр, порожденный
образующей
- действительный параметр, порожденный
образующей ![]() – посстоянное число. Глобальными инвариантами
этой группы являются
– посстоянное число. Глобальными инвариантами
этой группы являются
![]()
так
что инвариантное относительно группы сдвигов решение системы (3) имеет вид
![]()
определяющее
волну неизменного профиля, движущаяся с постоянной скоро-стью ![]() .
.
Выражая
производные от функции ![]() через произ-водные по
через произ-водные по ![]() ,
имеем,
,
имеем,
![]()
после
чего система (3) переходит к следующей системе обыкновенных дифференциальных
уравнений
![]() (5a)
(5a)
![]() (5б)
(5б)
а
граничные условия (4) к
![]() (6)
(6)
Уравнение
(2.5б) после двукратного интегрирования, с учетом условия на бесконечности
(6), дает
![]() (7)
(7)
После
подстановки (7) в
(5а) получим
![]() (8)
(8)
Последнего уравнения интегрируем используя формализацию
Хироты [1]. Подстановка ![]() - функции комплексные, в (8) и
последующее расщепление приводят к двум уравнениям
- функции комплексные, в (8) и
последующее расщепление приводят к двум уравнениям
![]() , (9а)
, (9а)
![]() . (9б)
. (9б)
Где ![]() есть оператор Хироты, определяемый по
формуле
есть оператор Хироты, определяемый по
формуле
![]() при
при
![]() .
.
В отличие от обычной для данного метода билинейной
формы, выражения (9) являются трилинейными, что
усложняют дальнейшие вычисления.
Отметим,что трилинейную формуХироты имеет
и уравнение Ландау-Лифщица [4]. Однако, как в этом убедимся ниже, возникшая
трудность не является принципиальной. Выражения (9) легко могут быть
преобразованы к билинейным формам Хироты [2].
Для построения солитонных решений уравнения (8), удовлетворяющих
граничному условию
(6), разложим функции
![]() в формальные ряды теории возмущений
в формальные ряды теории возмущений
![]() (10а)
(10а)
![]() (10б)
(10б)
где ![]() - некоторый действительный параметр.
- некоторый действительный параметр.
Подставив (10) в
(9), и приравняв к нулю коэффициенты
при каждой степени ![]() ,
получим:
,
получим:
![]() (11а)
(11а)
![]() (11б)
(11б)
![]() (11в)
(11в)
![]() (11г)
(11г)
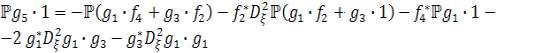 (11д)
(11д)
и т.д., где
через ![]() обозначены операторы
обозначены операторы
![]()
![]() .
.
Для солитонных решений ряды (10) обрываются.
Функция ![]() где
где ![]() -
комплексные числа, является решением уравнения (11а), если имеет место
равенство
-
комплексные числа, является решением уравнения (11а), если имеет место
равенство
![]() (12)
(12)
Тогда
из (11б), интегрируя, найдем
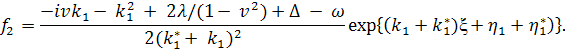
Уравнение
для ![]() (11в), после подстановки в него
(11в), после подстановки в него
![]() примет вид
примет вид![]() Следовательно, в силу линейности оператора,
можно взять
Следовательно, в силу линейности оператора,
можно взять ![]() Аналогично, из (2.11г)
имеем, что
Аналогично, из (2.11г)
имеем, что ![]()
Далее нетрудно убедится в том, что все
уравнения для ![]() в (11) являются линейными однородными, так что возьмём
в (11) являются линейными однородными, так что возьмём
![]()
Таким образом, решением трилинейных
уравнений (9) являются
![]() (13)
(13)
где ![]() -
вполне определенные функции.
-
вполне определенные функции.
Теперь можно написать явный вид
солитонного решения системы (1). Из (12)
имеем, что
![]()
где
k - любое действительное число, и
![]()
Тогда в силу (13), по формулам ![]() (2), (7)
получим солитонное решение системы уравнений (1) удовлетворяющее граничному
условию (2):
(2), (7)
получим солитонное решение системы уравнений (1) удовлетворяющее граничному
условию (2):
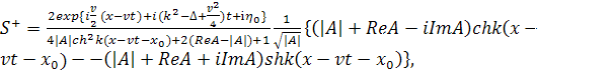
![]()
![]()
![]() - любые действительные числа.
- любые действительные числа.
Эти формулы
показывают, что
решение
![]()
представляет
собой уединенную волну, локализованную вдоль направления ![]() центр которой движется с постоянной
скоростью
центр которой движется с постоянной
скоростью ![]() .
.
Литература
1.Hirota R. Direct Methods of Finding Exact Solutions jf Nonlinear Evolution Equations. Вкн.:Baklund Trans formations, ed.by R.M. Miura, Lecture
Notes in Mathematics, 1976, Vol.515.
2.Hirota R. Bilinearization of Soliton Equations /J. Phys. Soc. Jap.,
1982, v.51, №1, p.323-331.
3.Мырзакулов Р. Новые
нелинейные эволюционные уравнения, описывающие динамику магнон-фононных систем
/Вестник АН Каз ССР, 1990, №1, с.74-77.
4.Богдан М.М., Ковалев
А.С. Точные многосолитонные решения уравнений Ландау-Лифщица для неизотропного
ферромагнетика /Писма в ЖЭТФ, 1980,т.31,№8, с.453-457.