Gaidar O. G., Pisanka E. S.
Ukraine, Donetsk National Technical University
INVERSION
OF SURFACES REFERRED
TO THE LINES OF CURVATURE
Reference of
surfaces to the lines of curvature plays an important role in the theory of
covers and at determination of optimum trajectories of processing on NC machine
tools. Transition from any parameterization to the special one, at which the
coordinate grid coincides with the grid of lines of curvature, is possible only
for some surfaces. It is connected with the fact that finding of the lines of
curvature on a surface is reduced to the solution of the differential equations
which can be integrated in some cases only. Considering this designing of the
surfaces and finding the families of the lines of curvature on them is a topical
task.
One of the most
widespread mathematical apparatuses of designing of lines and surfaces are
geometrical transformations. They allow to receive new images, keeping certain
useful properties of prototypes. The transformation of the known surfaces
referred to the families of the lines of curvature will be carried out using
the inversion. As far as this transformation is conformal, the orthogonality of
the lines remains constant and the lines of curvature of the initial surface
turn into the lines of curvature of the new surface [1].
If 
, 
, 
(1)
are the parametrical equations of
the prototype surface, the parametrical equations of the image surface,
received by application of the transformation of the inversion [2], are
,
,
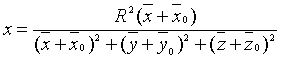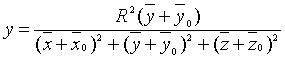(2)
,
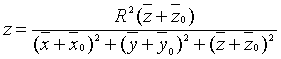where 
are the coordinates of the center of
inversion,
R is the radius of
inversion.
Thus, if t=const, u=const are the lines of the curvature of the surface (1), they are
the lines of curvature and for the surface (2) too.
Let's note a
number of properties useful to the applied formation of characteristics which
the inversion transformation has:
- the image of the sphere is the
sphere (we will remind that the plane is the sphere too and has the infinite
radius);
- the image of the plane which
passes through the center of inversion is the plane which passes through the
center too;
- the image of the plane which
doesn't pass through the center of inversion is the sphere which passes through
the center of inversion;
- the image of the sphere which
doesn't pass through the center of inversion is the sphere which doesn't pass
through the center of inversion;
- the image of the sphere which
passes through the center of inversion is the plane which doesn't pass through
the center of inversion;
- the transformation by inversion is conformal: it
keeps corners.
For example, tor surface of the
rotation (fig. 1), which equation is
, 
, 
(3)
where R is the radius of the circle of the centers of one-parametrical
family of the forming circles, r is the radius of the forming circle;
by transformation of the inversion
(2) is raised to the equation of the cyclide of Dupin of the fourth order
without conic points
,
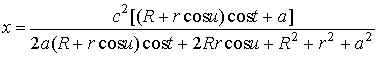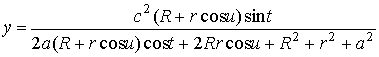, (4)
.
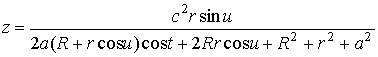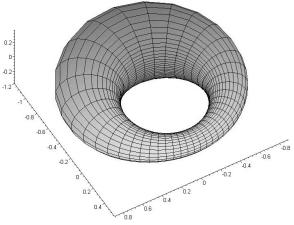
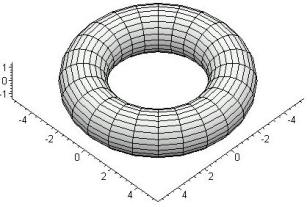
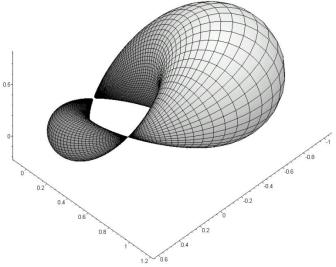
Fig. 1 –
The prototype surface Fig. 2 – The image surface
In fig. 2 this
cyclide constructed on the equation (4) at R=4, r=1.3, a=2.7, c=1,
, 0
£ t £ 2p, 0 £ u
£ 2p is shown.
Dupin's cyclide
of the fourth order with two conic points is possible to be received using the
inversion of the rotation cone provided that the center of the inversion is assumed
not to belong to its surface [3].
The parametrical equations of the
cone-prototype will be written down as
, 
, 
(5)
Let's
substitute (5) to (2) and receive
, 
,
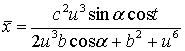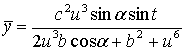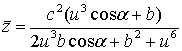(6)
the parametrical equations of the
cyclide of the fourth order with two conic points (fig. 3) at 
-
a tilt angle forming the cone-prototype to its axis, b = - 1 - distance from
the center of inversion to cone prototype’s top, c=4, 0 £ t £ 2p, –10
£ u £ 10.
At last, the
cyclide of the fourth order with one conic point is possible to be received
using the inversion of rotation of the cylinder concerning the sphere which
center is assumed not to belong to its surface [3]. The parametrical equations
of the cylinder are
, 
, 
. (7)
let's substitute to (2) and receive
, 
, 
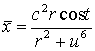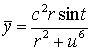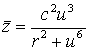(8)
the parametrical equations of the cyclide of the fourth order with one
conic point. This cyclide is shown in fig. 4 at r=6, c=5, 0 £ t £ 2p, –10 £ u
£ 10..
