Математика/5.
Математическое моделирование
Baimankulov A.
Kostanay State
University named after A.Baitursynov, Kazakhstan.
Rating the solution of
direct problem
In the area of ![]() we consider
the problem
we consider
the problem
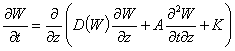 , (1)
, (1)
![]() ,
, ![]() (2)
(2)
![]() (3)
(3)
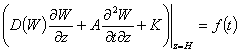 , (4)
, (4)
where
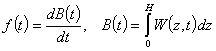 . (5)
. (5)
To determine ![]() moisture is
given on the soil surface
moisture is
given on the soil surface
![]() . (6)
. (6)
We multiply (1) on ![]() and integrate over
all internal points of the domain
and integrate over
all internal points of the domain ![]() then
then
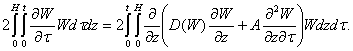
Integrating by parts with respect to variable, giving initial and boundary conditions (2) - (4) we obtain
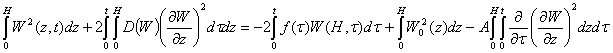
or
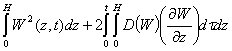 +
+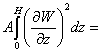
 +
+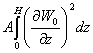
![]() .
.
After a series of obvious transformations we have
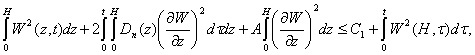 (6)
(6)
where
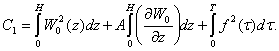
using the inequality
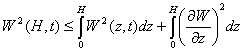 (7)
(7)
from (6) we obtain
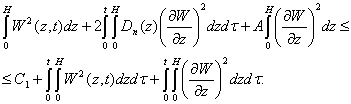
After application of the Gronwall lemma we
obtain the estimate
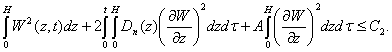
Based on this evaluation of (7) implies:
![]()
Lemma 1. if ![]() then for the solution of (1) - (4) we have the estimates:
then for the solution of (1) - (4) we have the estimates:
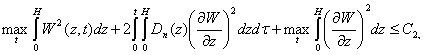
![]()
Consequence.
From the obvious equality
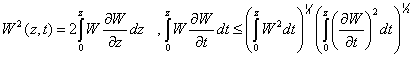
implies
the estimate
![]() .
.
Using
Lemma 1, we deduce the inequality:
![]() .
.
References
1.Нерпин С.В., Юзефович Г.И. О расчете нестационарного
движения влаги в почве// Доклады ВАСХНИЛ, № 6, 1966.
2.Юзефович Г.И., Янгарбер В.А. Исследование
нелинейного уравнения влагопереноса. // Л.: Колос. Сб. трудов по агрофизике,
вып. № 14, 1967.
3.Байманкулов А.Т. Определение коэффициента
капиллярной диффузии.// Материали за VIII международна научна практична конференция «Бъдещето
въпроси от света на науката -2012», т.36, 17-25 декември, 2012, София.