К.п.н., Петрова С.Н., Пирожок А.А.

Уральский государственный экономический университет, Россия

Применение векторных функций Ляпунова

к анализу устойчивости и агрегирования

сложных технически системы

Структура агрегирования и анализ устойчивости играют важную роль в задачах проектирования, совершенствования и при оценке безопасности функционирования сложной технической системы [1–6]. Структура агрегирования используется для получения эффективных критериев устойчивости. Смысл метода агрегирования состоит в замене исходной сложной системы системой меньшей размерности таким образом, чтобы решения исходной и полученной систем находились во взаимно однозначном соответствии. Корректность указанной замены является отдельной, часто трудной задачей, связанной с тем, что система n‑го порядка имеет n собственных движений, каждое из которых может происходить при определенной реализации структурных возмущений. Условия агрегирования сложной системы тесно связаны с характерными признаками исходной системы S.

В работе рассмотрена структура агрегирования, учитывающую взаимосвязи между агрегатами S_i . Пусть функция v_i является i‑й компонентой вектор-функции Ляпунова V = (v₁, v₂, ¼, v_k)¢, причем

, или

Структура агрегата базируется на условии, приведенном ниже.

Условие 1. Существуют открытые связные окрестности N_i , , состояния x_i = 0, функции v_i и z_i : R´R ® R, действительные числа a_ij(A_i), b_ij(A_i) и c_ij такие, что

1) a_ij(A_i) ³ 0, i ¹ j, b_ij(A_i) ³ 0, c_ij ³ 0 "i, jÎ[1, k], "AÎG^k ;

2) v_i – положительно определенные на N_i  "i = 1, 2, ¼, k;

3) ;

4)

где 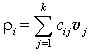, "i = 1, 2, …, k;

5) , "i = = 1, 2, …, k; "(t, x, P, A)Î;

6) существуют такие числа a_ij, b_ij, и , где A^*ÎG^k  , для которого справедливы оценки

a_ij(A_i) £ a_ij, b_ij(A_i) £ b_ij , "i, j = 1, 2, ¼, k; "AÎG^k .

Данная структура агрегирования вводит матрицы сравнения A = (a_ij), B = (b_ij) и C = (c_ij), где А, В, СÎR^k´k, и вектор-функции сравнения z = (z₁, z₂, ¼, z_k)¢ и r = (r₁, r₂, ¼, r_k)¢.

Условия 4) – 6) приводят к дифференциальному неравенству:

V ^*(t, x, P, A) £ AV(t, x) + BZ(r), r = CV(t, x),

"(t, x, P, A)Î, или V ^* £ AV + BZ(r), r = CV. (1)

Пусть K = diag {k₁, k₂, ¼, k_k }. Справедливы следующие признаки устойчивости.

Утверждение А. Если а) выполняется условие 1;

б) существуют положительные числа x_i (или x_i = +¥) такие, что множества V_i z(t) асимптотически сжимающиеся при каждом zÎ]0, x_i [ и каждом i = 1, 2, …, k;

в) матрицы B = (b_ij) или C = (c_ij) имеют положительную диагональ;

г) пара (А, В) – управляема, пара (А, С) – наблюдаема, а матрица А – устойчива;

д) существует неотрицательная диагональная k´k-матрица Q такая, что матрица

Q(w²) = K ^–1 + Н_i (I + jwQ) С (А – jwI)^–1 В (2)

положительно определена при каждом wÎ[0, +¥], то состояние x = 0 системы

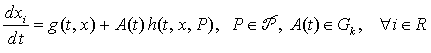⁽³⁾

структурно асимптотически устойчиво на P ´G^k .

Матрицы A, B и C, а также величина v – известные вещественные величины. Для несвязанных агрегатов

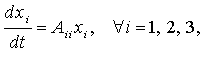(4)

функции v_i выбираем в виде где H_i – решения матричных уравнений Ляпунова

. (5)

Здесь G_i – произвольные положительно определенные симметричные матрицы.

Если условия а) – г) выполнены при , x_i = +¥ и функциях v_i , радиально неограниченных при "i = 1, 2, …, k, то состояние ^.x = 0 системы (3) структурно асимптотически устойчиво в целом на P ´G^k .

Утверждение Б. Если а) выполняется условие 1;

б) функции v_i – убывающие на N_i  "i = 1, 2, …, k;

в) одна из матриц B = (b_ij) или C = (c_ij) имеет положительную диагональ;

г) пара (А, В) является управляемой, пара (А, С) является наблюдаемой, а матрица А – устойчивой;

д) существует неотрицательная диагональная (k´k)‑матрица Q такая, что матрица Q(w²), положительно определена при каждом wÎ[0, +¥], то состояние x = 0 системы (3) структурно равномерно асимптотически устойчиво на P ´G^k .

Если условия а) – д) выполняются при и функции v_i – радиально неограниченные при всех i = 1, 2, …, k, тогда состояние x = 0 системы (3) структурно равномерно асимптотически устойчиво в целом на P ´G^k .

Отметим, что данная структура агрегирования эффективна лишь в случае, когда существует значение iÎ{1, 2, …, k}, для которого k_i = +¥. В противном случае все k_i < +¥ и, следовательно, так как k_i > 0 и b_ij > 0, дифференциальное неравенство (1) принимает вид

.

Пример. Рассмотрим систему S, описываемую уравнениями шестого порядка (n_i = 2, i = 1, 2, 3; s = 3):

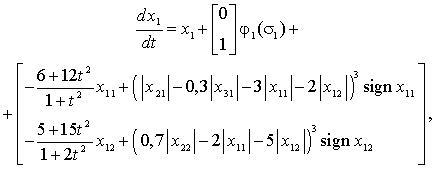
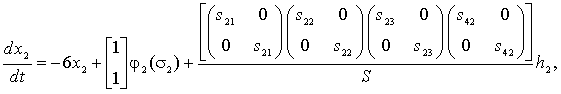
где ;

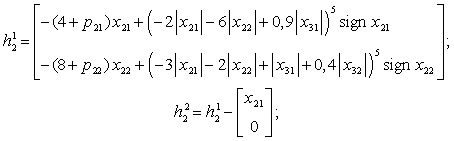
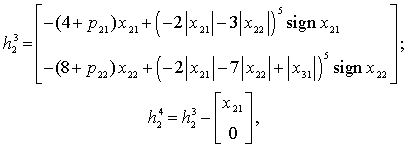
и

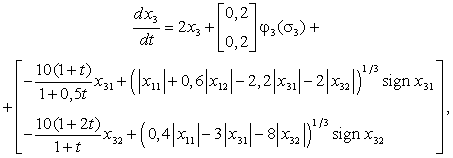
где

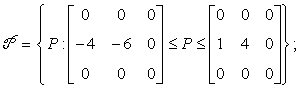
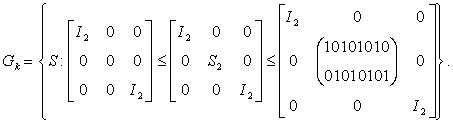
Независимые агрегаты описываются уравнениями

,

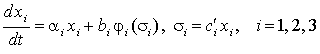решения x = 0 первого и третьего из которых неустойчивы. Структура взаимосвязей дает возможность выбрать функции v_i в виде

,

причем

,

где A = –2I, B = 2I; r = (r₁, r₂, ¼, r_k)¢; ;

k_i = +¥, i = 1, 2, 3;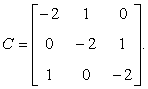

Откуда получаем

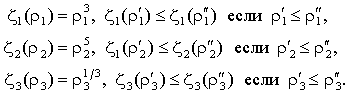
Следовательно, все условия требования 1 выполняются. Кроме того, пара (А, В) является управляемой, пара (A, С) – наблюдаемой, а матрица А – устойчивой. Пусть . Тогда имеем

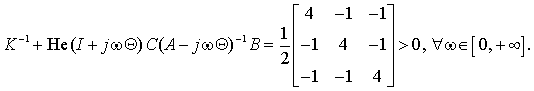
Согласно критерию 2 состояние x = 0 полной системы структурно равномерно асимптотически устойчиво в целом на P ´G^k при допустимых нелинейностях в секторе [0, +¥].

Таким образом, критерий устойчивости установлен на основе системы сравнения третьего порядка, в то время как исходная система имеет шестой порядок. Используемая при этом вектор-функция Ляпунова имеет вид

.

Рассмотрены специальные случаи структуры агрегатов. Разработаны алгоритмы анализа устойчивости на базе приведенных выше условий устойчивости с учетом рассмотренной структуры агрегатов. Рассмотрены модели манипуляционных робототехнических систем с применением метода агрегирования. Для систем предикатного управления [7] даны обобщения условий устойчивости на основе применения функций Ляпунова. Настоящая работа является продолжением работ [8, 9].

Работа выполнена при поддержке РФФИ (проект № 13-08-00710).

Литература:

1. Бусленко Н.П. Моделирование сложных систем, М.: Наука, 1978.

2. Воронов А.А. Введение в динамику сложных систем. М.: Наука, 1985.

3. Груйич Л.Т., Мартынюк А.А., Риббенсон-Павелла М. Устойчивость крупномасштабных систем при структурных и сингулярных возмущениях. Киев: Наук. думка, 1984.

4. Мартынюк А.А. Устойчивость движения сложных систем. Киев: Наукова думка, 1975.

5. Мартынюк А.А., Като Дж., Шестаков А.А. Устойчивость движения: метод предельных уравнений. Киев: Наукова думка, 1990.

6. Матросов В.М. Метод векторных функций Ляпунова: анализ динамических свойств нелинейных систем. М.: Физматлит, 2001.

7. Васильев С.Н. К интеллектному управлению // Нелинейная теория управления и ее приложения. М.: Физматлит, 2000. С. 57–126.

8. Петрова С.Н. Об условиях устойчивости и построении моделей сравнения для крупномасштабных систем // Труды XXI Международной конференции «Проблемы управления безопасностью сложных систем» (Москва, 18 декабря 2013 г.). М.: ИПУ РАН, 2013. С. 41–45.

9. Петрова С.Н. Анализ устойчивости дискретных управляемых систем с неполной информацией // Наукоемкие технологии. 2012. № 1. Т. 13. С. 42–46.