О простейшем методе решения уравнения параболического типа второго порядка
Бейсенова А. Е. –
магистрант II – го курса, Государственного
университета имени Шакарима, г. Семей, Казахстан
Рассмотрим два
уравнения параболического типа
![]() (1)
(1)
![]() (2)
(2)
Общее решение уравнений
(1) и (2) соответственно может быть записано в виде
![]() (
(![]() )
)
![]() (
(![]() )
)
где ![]() - постоянные,
- постоянные, ![]() - произвольные функций. Опираясь к дополнительным условиям,
находим частные решения этих уравнений.
- произвольные функций. Опираясь к дополнительным условиям,
находим частные решения этих уравнений.
Покажем, что с помощью разных преобразований уравнений
зависимых от характеристик, уравнения в
частных производных приводятся к дифференциальным уравнениям, и можно получить общее решение
зависимых от некоторых постоянных.
Для отыскания частного
решения (1)
уравнения сделаем замену
переменных:
![]() (3)
(3)
и получим
![]() (4)
(4)
дифференциальное уравнение. Решив
это уравнение, переходя к прежним переменным находим частное решение
![]() .
(5)
.
(5)
Опираясь к дополнительным
условиям находим ![]() -постоянных.
-постоянных.
Рассмотрим для (1) уравнения задачу
Гурса
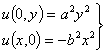 (6)
(6)
где ![]() . Итак решение
будет в виде
. Итак решение
будет в виде
![]() .
(7)
.
(7)
Если используем (6)
условие к общему решению (![]() ) уравнения (1), то
увидем,что полученное решение будет правильным.
) уравнения (1), то
увидем,что полученное решение будет правильным.
Теперь для (1) уравнения рассмотрим задачу Коши
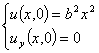 (8)
(8)
Если к (5)-ому уравнению
используем условия (8)-го уравнения, то получим
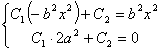
Из этого находим, что ![]() .
.
Таким образом, искоемое
решение имеет вид
![]() (9)
(9)
Теперь опираясь к этому условию, нахождение общего решения (![]() ), функций
), функций ![]() приводит к нашему
правильному рассуждению.
приводит к нашему
правильному рассуждению.
Характеристикой (2)-го уравнения
будет кривая в виде
![]() (10)
(10)
Отсюда, заменив на
![]() или
или ![]()
уравнение приводится к дифференциальному уравнению (4).
Итак решение будет в виде
![]() .
(11)
.
(11)
Если к уравнению (2) рассмотрим
задачу Коши
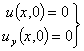 (12)
(12)
отсюда можно легко найти постоянных![]() .
.
Если решим эту задачу с
помощью общего решения, то возникло бы немного недоразумений.
Итак были показаны, что с
помощью рассматриваемых преобразований можно быстро найти частное решение в
некотором случае задачи основанных на краевые или начальные условия уравнения параболического типа.
Әдебиеттер:
1. А.В. Бицадзе, Д.Ф.
Калиниченко. Сборник задач по уравнениям математической физики. М: «Наука»
1977, 274 стр.