Брюхов В.Ю.

Лесосибирский Педагогический институт филиала Сибирского федерального университета

Применение композиции движений к решению задач на построение

Вопрос о применении геометрических преобразований к решению задач на построение достаточно подробно исследован. Суть метода геометрических преобразований заключается в следующем: наряду с данными и искомыми фигурами рассматривают их образы или образы их частей с тем, чтобы, построение стало проще или даже свелось к какой-либо элементарной задаче [1: 93]. Однако при решении ряда задач возникает необходимость в использовании не одного, а нескольких геометрических преобразований последовательно, т.е. композиции преобразований.

Задача 1. Построить треугольник по серединным перпендикулярам к сторонам треугольника и радиусу описанной окружности.

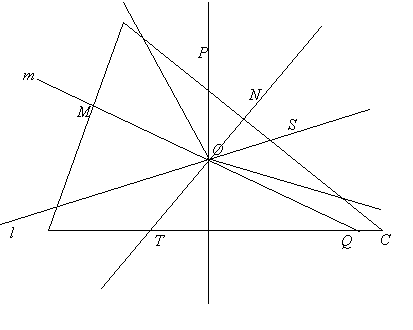0Пусть m, n и k – серединные перпендикуляры к сторонам АВ, ВС и АС соответственно, причем mnk = O , R – радиус описанной окружности. B = S_m( A ) , C = S_n ( B ) , A = S_k( C), т.е. композиция осевых симметрий S_m˚ S_n ˚ S_k переводит точку А в себя. Точка О также инвариантна как точка пересечения осей. Композиция трех осевых симметрий, имеющая инвариантные точки, есть осевая симметрия с осью, проходящей через эти точки, т.е. S_m˚ S_n˚ S_k = S_OA. Пусть m∩ AB = M, m ∩ AC = Q, n ∩ BC = N, n ∩ AC = T, k ∩ AC= K, k ∩ BC = P, OA ∩ BC = S. Тогда из свойств осевой симметрии: ÐАОМ = ÐМОВ, ÐАОК = ÐСОК , ÐВОN = ÐNOC (1). ÐМОВ = ÐМОР – ÐВОР, с учетом равенства (1) ÐВОР = ÐМОР – ÐАОМ (2);

аналогичноÐСОQ = ÐАОТ + ÐТОК – ÐQOK (3);

ÐBON = ÐBOP + ÐPON,ÐNOC=ÐNOS+ÐSOC,

ÐSOC=ÐSOQ–ÐCOQÐВОР+ ÐРОN = ÐNOS + ÐSOQ–ÐCOQ( 4).

Подставим выражения (2) и (3) в равенство (4):

ÐМОР – ÐАОМ + ÐРОN = ÐNOS + ÐSOQ – ÐAOT–ÐТОК + ÐQOK.

Но ÐPON = ÐAOT, ÐAOT = ÐNOS, ÐSOQ = ÐMOA, ÐMOP = ÐKOQ (как вертикальные). Тогда 2ÐPON = 2ÐАОМÐPON = ÐAOM или Ðk,n = ÐOA,m.

Проведенный анализ приводит к следующему построению: через точку О проводим прямую l, образующую с прямой m угол, равный углу между прямыми k и n; окружность с центром в точке О радиусом R пересекает l в точке А; вершины С и В строятся как образы точки А при симметрии относительно прямых k и n соответственно.

Задача 2: Построить квадрат по четырем точкам, по одной на каждой стороне квадрата.

Пусть данные точки M, N, K, L лежат соответственно на сторонах квадрата АВ, ВС, 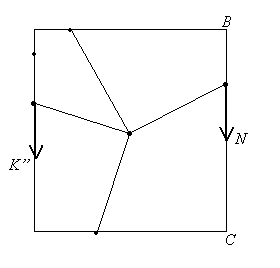251662336251665408251664384251663360CD, AD. При повороте на угол 90^◦вокруг центра квадрата точка М, лежащая на стороне АВ, перейдет в точку М’, лежащую на стороне ВС, а точка К на стороне CD – в точку К’ на стороне AD. Если затем осуществить параллельный перенос на вектор , то в результате композиции точка М перейдет в точку N, а точка К’ перейдет в точку К”, также лежащую на AD. Но композиция поворота и параллельного переноса есть поворот на тот же угол, поэтому задача сводится к нахождению поворота на угол 90^◦, переводящего М в N. Центр поворота О удовлетворяет условиям: 1) он равноудален от точек М и N, следовательно, принадлежит серединному перпендикуляру к отрезку МN; 2) он принадлежит окружности, построенной на МN как на диаметре, т.к.MON= 90^◦.

Проведенный анализ приводит к следующему построению: на отрезке MN строим окружность как на диаметре, строим прямую l₁, как серединный перпендикуляр к MN; прямая l₁ и окружность w пересекаются в точке О; при повороте точки K вокруг точки О на 90⁰ получаем K^” , K^”L - прямая; проводим прямую k через точку K и перпендикулярно прямой K^”L; прямые K^”L и k пересекаются в точке D; проводим прямую m через точку M перпендикулярно _{, прямые m и пересекаются в точке A}; строим прямую n через точку N и перпендикулярно m, прямые m и n пересекаются в точке B, n и k пересекаются в точке C; ABCD – искомый.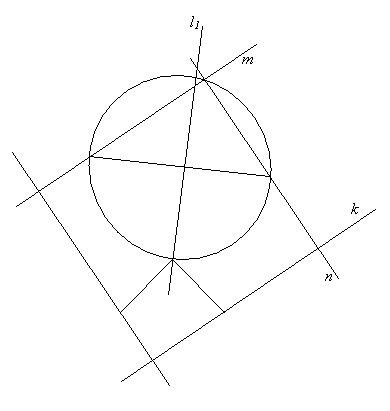251669504

Рассмотренные задачи предполагают и другие решения, однако решение с использованием свойств композиции преобразований более изящно и рационально.

Литература:

1. Аргунов, Б.И. Геометрические построения на плоскости / Б.И. Аргунов, М.Б. Балк. – М.: Учпедгиз, 1955.- 270 с.

2. Заславский А.А. Геометрические преобразования. М.: МЦНМО, 2003. 86 с.