Хуанган Н., Исабек Т.К., Демин В.Ф.

Қарағанды мемлекеттік техникалық университеті, Қазақстан

Ходжаев Р.Р.

ЖШС «ГеоМарк» ғылыми зерттеу орталығы, Қазақстан

Қазба контуры жанындағы кен жынысындағы жарықшақтар дамуының бастапқы жылдамдығы жайлы

Контр-бөлшектердің қозғалысы кезінде қатты денеде болатын процестерді сипаттау үшін есептеу (санап шығару) жүйесін басшылыққа алу керек, ол дегеніміз қазба контуры жанындағы кен жынысындағы контр-бөлшектердің орналасуын осы жүйемен байланысты және уақытты көрсету үшін қызмет ететін сағатпен белгілеуге арналған координаталар жүйесі болып табылады. Келесі ой-пікірлерімізді инерциялық есептеу (санап шығару) жүйесі үшін жүргіземіз.

Материалдық бөлшектердің өзара әрекеті қалыпты механикада бөлшек координаталарының қызметі болып табылатын потенциалдық өзара әрекеттесу арқылы сипатталады. Өара әрекеттесуді сипаттауға арналған бұл тәсіл бір сәтте таралады деген болжалға ие, өйткені әр контр-бөлшекке әр уақытта басқаларынан әсер ететін күш бөлшектердің осы уақыттағы жағдайына байланысты болады.

Алайда тәжірибе көрсеткендей, табиғатта сәттік өзара әрекеттесулер болмайды. Сондықтан өзара әрекеттесудің бір сәтте таралуы туралы болжалдан туындайтын механикада да белгілі бір дәлсіздік бар. Турасында, егер өзара әрекеттесуші дененің бірінде қандайда бір өзгеріс болса, онда басқа денеде бұл өзгеріс белгілі бір уақыт өткеннен кейін ғана көрінеді. Тек осы уақыт мерзімінен кейін екінші денеде осы өзгерістен туындаған процестер жүре бастайды. Екі дене арасындағы қашықтықты осы уақыт мерзіміне бөлсек, өзара әрекеттесу таралымының жылдамдығын аламыз.

Бір бөлшектен басқаға таралатын өара әрекеттесуді бірінші бөлшектен берілетін және екіншіге бірінші бөлшек өткерген өзгерістер жайлы «білуге мүмкіндік беретін» «сигнал» деп те түсіндіреді. Өзара әрекеттесу таралымының жылдамдығын «сигнал жылдамдығы» деп те атайды.

Серпімді шексіз изотропты денедегі өзара әрекеттесу таралымының жылдамдығы онда кернеу түріне байланысты болады. Бөлшекке қалыпты кернеу әсер еткен кезде бұл жылдамдық серпімді бойлық толқын таралымының жылдамдығына с_р, ал жылытушы кернеу әсер еткенде көлбеу толқын жылдамдығына с_S тең болады. 1-суретте қатты денеде әрекет ететін кернеудің негізгі түрлері көрсетілген.

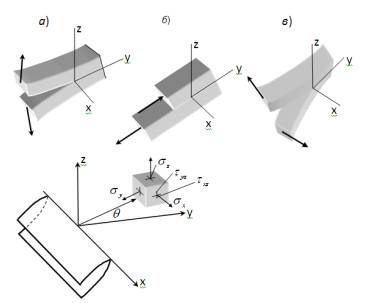
1-сурет – Жарықшақ жанындағы кернеу түрлері

а) жарушы кернеу ; б) жанама кернеу ; в) бойлық кернеу .

Келесі пікірлерімізде біз оқиға түсінігін қолданатын боламыз. Оқиға болған орнымен және болған уақытымен анықталады. Осылайша, қатты денедегі контр-бөлшек оқиғасы осы бөлшектің үш координатасымен және оқиға болған уақыт мерзімімен анықталады.

Бір-біріне қатысты тұрақты жылдамдықпен жылжитын О және О^/ сияқты екі есептеу (санап шығару) жүйесін қарастырайық. Координаталық осьтерді мынадай етіп аламыз: x және x^/ осьтері беттсу керек, ал y және z осьтері, сәйкесінше y^/ және z^/ осьтері де параллель болу керек; уақытты t және t^/ деп белгілейміз.

Бірінші оқиғада О координаталар жүйесінде x₁, y₁, z₁ координаталары бар нүктеден бойлық немесе көлбеу толқын жылдамдығымен таралатын сигнал t₁ уақыт мерзімінде дәл осы жүйеде жіберілген болсын делік. О жүйесіндегі осы сигнал таралымын қарастырайық. Ал екінші оқиғада сигнал t₂ уақыт мерзімінде x₂, y₂, z₂ нүктесіне келсін делік. Сигнал с_р немесе с_S жылдамдықпен (әрі қарай жылдамдықты с_рS деп белгілейміз, бұл жылдамдықты сигналдар бірінің таралу жылдамдығы деп түсіну керек) таралады; оның өткен қашықтығы тең. Басқа жағынан дәл осы қашықтықтең. Бұдан О жүйесіндегі екі оқиғаның координаталары арасында мынадай тәуелділік пайда болады:

. (1)

Бұл екі оқиғаны, яғни сигналдың таралуын О^/ жүйесінен де көруге болады. О^/ жүйесіндегі бірінші оқиға координаталары: , ал екінші оқиға координаталары: болсын делік, и так как система отсчета О есептеу (санап шығару) жүйесі О^/ жүйесіне қатысты (v – екі инерциялы жүйенің салыстырмалы жылдамдығының абсолюттік шамасы) жылдамдықпен қозғалатындықтан, екі оқиғаның координаталары арасындағы тәуелділік О^/ жүйесінен қарағанда мынаған тең болады:

. (2)

Осылайша, О жүйесіндегі сигнал таралымының өзара жақын ек оқиғасының арасындағы интервал дәл осы жүйеден қарағанда:

, (3)

ал О^/ жүйесінен қарағанда:

(4)

тең болады.

Оқиғалар арасындағы интервалды есептеуге арналған (3) мен (4) формулалардан бақағанымыздай, О жүйесіндегі оқиғалар арасындағы интервал нөлге тең болса (оқиға болмаса), онда О^/ жүйесіндегі оқиғалар арасындағы интервал есептеу (санап шығару) жүйесінің инерциялығына тең () болады, яғни болса, онда болады. Басқа жағынан алғанда, пен - бірдей тәртіпте шексіз аз мәндер. Бұдан көретініміз, пен бір-біріне пропорционал болу керек:

,

Сонымен бірге а коэффициенті екі инерциялы жүйенің салыстырмалы жылдамдығының абсолюттік шамасына тәуелді бола алады. Ол координаталар мен уақытқа тәуелді бола алмайды, онда әр түрлі кеңістік пен сәт нүктелері тең болмас еді, бұл кеңістік пен уақыттың біртектілігіне қайшы келеді. Сонымен қатар ол салыстырмалы жылдамдық бағытына да тәуелді бола алмайды, өйткені бұл кеңістік изотроптығына қайшы келер еді.

Үш есептеу (санап шығару) жүйесін О, О₁, О₂ қарастырайық, мен - О₁ және О₂ жүйелерінің О жүйесіне қатысты қозғалыс жылдамдығы болсын. Онда

.

Дәл сондай негіздемемен былайша жазуға болады:

,

мұнда V₁₂ – О₂ жүйесінің О₁ жүйесіне қатысты қозғалыс жылдамдығының абсолюттік шамасы. Оларды салыстыра отырып, табатынымыз

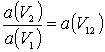. (5)

Алайда V₁₂ және векторларының абсолюттік шамаларына ғана емес, сонымен бірге олардың арасындағы бұрышқа тәуелді. Сонымен қатар соңғысы қатынастың (5) сол жақ бөлігіне мүлдем енбейді. Сондықтан бұл қатынас егер функциясы осы қатынаста көрсетілгендей бірге тең болып, тұрақты шамаға айналса ғана дұрыс болады. Осылайша,

, (6)

Ал шексіз аз интервалдар теңдігінен соңғы интервалдар теңдігі де шығады: .

Бізге қатысты еркін қозғалатын сағатпен инерциялы есептеу жүйесін басшылыққа алып отырмыз делік. Әр уақыт мерзімінде бұл қозғалысты біркелкі деп қарауға болады. Сондықтан әр уақыт сәтінде қозғалыстағы сағатпен қозғалыссыз байланыста болатын координаталар жүйесін енгізуге болады, координаталар жүйесі де (сағатпен бірге) инерциялы есептеу жүйесі болады.

Шексіз аз уақыт мерзімінде dt (қозғалыссыз, яғни бізбен байланысты сағат бойынша) қозғалатын сағаттың жүріп өтетін қашықтығы: . Қозғалыстағы сағатпен байланыста болатын координаталар жүйесінде соңғылары нөлге тең болады: . Интервалдың инварианттылығының әсерінен

,

бұдан .

формуласындағы v қозғалыстағы сағат жылдамдығы болып табылатындықтан, онда

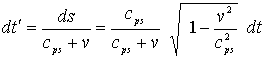. (7)

Бұл формуланы интегралдап, қозғалыссыз сағат бойынша уақыт өткендегі жылжымалы сағат көрсететін уақыт аралығын табуға болады:

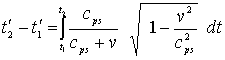. (8)

Сағат бойынша есептелетін, берілген объектімен бірге қозғалатын уақыт осы объектінің меншікті уақыты деп аталады. (7) және (8) формулалары есептеу (санап шығару) жүйесінің уақыты арқылы меншікті уақытты көрсетеді, ал қозғалыс осы уақытқа қатысты қарастырылады.

(7) немесе (8) формуладан қозғалыстағы объектінің меншікті уақытының қозғалыссыз жүйедегі сәйкес келетін уақыт мерзімінен әрдайым төмен болатындығын көреміз.

Сағат көрсететін уақыт аралығы осы сағаттың геодезиялық сызығына бойлай алынған 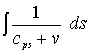интегралына тең. Біз ұсынып отырған жағдай үшін геодезиялық сызық төрт өлшемді болып табылады. Төрт өлшемді геодезиялық сызық – контр-бөлшектердің кеңістіктік-уақыттық траекториясы болып табылатын кеңістік-уақыттағы сызық. Егер сағат қозғалыссыз болса, онда оның геодезиялық сызығы тік, уақыт осіне параллель болады; ал егер сағат тұйық жолмен біркелкісіз қозғалып, бастапқы орнына қайтып келсе, онда шеодезиялық сызық қозғалыссыз сағаттың әлемдік тік сызығындағы қозғалыс басы мен соңына сәйкес келетін екі нүкте арқылы өтетін қисық болады. Басқа жағынан алғанда, біз тыныштықта тұрған сағаттың, қозғалыстағы сағатқа қарағанда, әрдайым үлкен уақыт аралығын көрсететіндігін байқадық. Осылайша мынадай шешімге келеміз: берілген екі нүкте аралығынан алынған интегралы осы екі нүктені біріктіретін тік геодезиялық сызық бойынша алынса, ең үлкен мәнге ие болады.

Контр-бөлшектер қозғалысын зерттеген кезде ең аз әрекет принципін басшылққа аламыз. Бұл принцип бойынша: кез-келген механикалық жүйеде әрекет деп аталатын интеграл S болады, ол іс жүзіндегі қозғалыс үшін минимум болады да, оның вариациясы сәйкесінше нөлге тең болады.

Еркін контр-бөлшектің, яғни сыртқы күш әсеріне түспейтін контр-бөлшектің әрекет интегралын анықтайық. Бұл интеграл қандай да бір инерциялы есептеу жүйесін таңдауға тәуелді болмау керектігін атап өткен жөн. Бұдан байқайтынымыз, ол скалярдан алыну керек. Әрі қарай интегралда бірінші дәрежелі дифференциалдар тұру керектігі белгілі. Алайда немесе интервалы еркін материалдық бөлшекке тұрғызуға болатын жалғыз скаляр болып табылады, мұндағы - біршама тұрақты.

Сонымен еркін бөлшектегі әрекет мынадай болу керек:

,

мұнда интеграл a және bберілген екі оқиға арасындағы әлемдік сызықты бойлай – t₁ және t₂ уақытта бөлшекті бастапқы және соңғы орында табумен алынады; b - осы бөлшекті сипаттайтын біршама тұрақты. Барлық бөлшек үшін b тұрақты шама болу керектігін оңай аңғаруға болады. Шындығында, ертеректе атып кеткеніміздей, интегралы геодезиялық тік сызыққа бойлай максимал мәнге ие. Геодезиялық қисық сызыққа бойлай интегралдай отыра, оны қажетінше азайтуға болады.

Сонымен оң белгісі бар интеграл минимумға ие бола алмайды; ал теріс белгісі бар интегралда минимум болады (әлемдік тік смызыққа бойлай).

Әрекетті уақыт бойынша интегралдау түрінде көрсетуге болады:

.

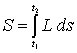L коэффициенті dt кезінде осы механикалық жүйе үшін Лагранж функциясы болып табылады. (3) формуласының көмегімен табатынымыз

,

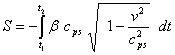мұнда v – контр-бөлшек жылдамдығы. Бөлшекке арналған Лагранж функциясы сәйкесінше

.

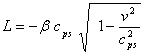b шамасы, атап өткеніміздей, берілген бөлшекті сипаттайды. Классикалық механикада кез-келген бөлшек оның массасымен m сипатталады. b және m шамаларының байланысын анықтайық. Ол шексіздікке өту кезінде L мәнін табуға арналған формуламыз классикалық формулаға ауысқан кезде табылады:

. (9)

Бұл өтуді жүзеге асыру үшін L-ді деңгейлері бойынша қатарға қояйық. Сонда жоғары дәрежелі мүшелерді алып тастай отыра алатынымыз

.

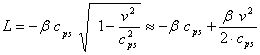Лагранж функциясының тұрақты мүшелері қозғалыс теңдіктерінде көрсетілмей, түсірілуі мүмкін. L орнына тұрақты мәнін түсіріп, классикалық формуламен (9) салыстырсақ, табамыз.

Осылайша, еркін материалдық бөлшек әрекеті

, (10)

Ал Лагранж функциясы

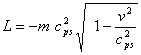. (11)

Вектор бөлшек импульсі болып табылатындығы белгілі ( - вектордың символдық белгіленуі). (7) формуласының көмегімен табатынымыз

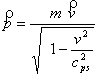. (12)

Жылдамдық төмен болған жағдайда () немесе шекте формула (11) ньютондық механикадағы қалыпты мәнге ие болады. Егер болса, онда импульс шексіздікке ие болады.

Уақыт бойынша импульстан бөлшекке әсер ететін күш болады. Бөлшек жылдамдығы бағыт бойынша өзгерсін, яғни күш жылдамдыққа перпендикуляр болсын. Онда

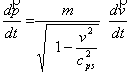. (13)

Ал егер жылдамдық шама бойынша ғана өзгерсе, яғни күш жылдамдық бойынша бағытталса, онда

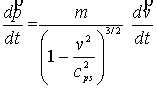. (14)

Осылайша, екі жағдайда да күштің жылдамдыққа қатынасы әр түрлі.

Бөлшек энергиясы мына формула бойынша анықталады [122]

.

L мен орнына (11) және (12) формулаларын қойғанда алатынымыз

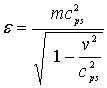. (15)

Бұл формуладан көретініміз, еркін контр-бөлшек энергиясы болғанда нөлге айналмайды, соңғы шама болып қалады, ол мынаған тең

. (16)

Мұны контр-бөлшек тыныштығының энергиясы деп атауға болады.

Аз жылдамдық кезінде () (15) формуласын дәрежесі бойынша жіктеу арқылы алатынымыз

, (17)

Яғни тыныштық энергиясын шегеріп, бөлшектің кинетикалық энергиясына арналған классикалық формулаға қол жеткіземіз.

Контр-бөлшектің массасын анықтау үшін (16) формуласына контр-бөлшек энергиясының формуласын (1) қояйық, бұл жағдайдағы ескеретін жайт: жарықшақ ұзындығы болу керек (с₀ – массивте басынан болған жарықшақтар ұзындығы)

. (18)

Бұдан контр-бөлшектің тыныштық энергиясы оның беттік жарықшақ пайда болу энергиясына тең болады, ол (4.39) формуладан анықталады.

Контр-бөлшек массасының мәні бар, енді оның бастапқы жылдамдығының қалай өзгергендігін анықтайық, ол үшін бұрышта өтетін радиус-векторды бойлай, тез өтетін бастапқы үдету процесі аяқталғаннан кейін есептеу керек және келесі бастапқы мәндерді басшылыққа алу керек: ; ; ; ; ; ; ; ; ; .

Есептеу нәтижелері 4.3-суретте берілген, онда жарықшақтар ұшының қашықтықтан тоннель контурына дейінгі бастапқы жылдамдығы (старттық үдеуден кейін) көрсетілген.

Бұзылыстың барлық түрлері үшін жарықшақтың таралу жылдамдығының көлбеу толқын таралымының жылдамдығымен әрдайым байланысты екендігін айта кеткен жөн, бұл көлбеу және бойлай жылжу кернеуі кезінде автоматты түрде пайда болады. Бір осьті созылу кезінде бұзылыс, 1-бөлімде айтылғандай, жанама кернеу аумалы күйдегі мәнге жеткенде (үшінші беріктік гипотезасы) болады, яғни бұзылыс жанама кернеу әсерінен болады, сәйкесінше осындай типті бұзылыс үшін болады.

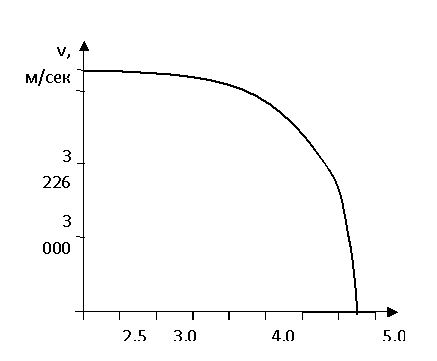
2 – сурет – бастапқы жылдамдық қатынасы

Осы ережелерге сүйенсек, лақтырыс қауіптілігін сейсмоакустикалық бақылау экспресс-әдісімен сейсмоимпульс уақытын тіркеуге қатысты айтарлықтай жағымды нәтижелер бар. Осы жұмыс нәтижесі бойынша ЗУА-4 типті дыбыс сезу аппаратурасы үшін геофон әрекетінің радиусы шахталық жағдайдағы сараптамалық тексерулерге кезінде – 20-30 м. Сейсмоимпульстерді тіркеу уақыты мин. Обоснование столь длительного времени регистрации сейсмоимпульсов в [123]-тегі сейсмоимпульстерді тіркеу уақытының осынша ұзақ болуының себебі аз деформация кезінде серпімділік пен жылжығыштық теориясының кеңістіктік мәселелер шешу негізінде алынды.

Қазбаның бойлық осін бойлай забой деформациялануы мынадай болады:

, (19)

мұндағы А мен В – константалар.

Деформацияның уақытқа өзгеруін есептеу үшін ауыспалы модульдер әдісін қолданайық. Онда (19) мынадай болады:

, (20)

мұнда 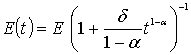; a , d - жылжығыштық параметрлері; t – уақыт.

Уақты t = 0 болғанда e = 0,05 %. Уақыт t = 5 минут болғанда e = 0,056 %, t = 10 мин болғанда e = 0,056 %.

Яғни алғашқы 5 минутта деформация 10 %-ға артады, ал келесі 5 минутта тек 1 %-ға артады.

Жарықшақтың пайда болу процесі деформация процесінің жүруімен түсіндірілетіндігі белгілі. Деформация уақыт өте келе әлсірейтіндіктен, жарықшақтың пайда болуында да, акустикалық эмиссия қарқындылығында да осындай әлсіреу болады. Комбайнды тоқтатқаннан кейінгі алғашқы 5 минутта тіркеу интервалы ақпарат алу үшін толығымен жеткілікті.

Алайда біздің пікіріміз бойынша (2-сурет), кен қазбасының контурынан белгілі бір қашықтықта (для приведенных условий это 3,77 м, т. е. в диапазоне действия геофона) әлсіз жарықшақтардың таралу жылдамдығы өзінің бастапқы даму кезеңінде қажетінше аз шамаға ие бола алады, - міне, дәл осы жағдаймен немесе или дополнительно к рассуждениям приведенным в [1]-те келтірілген пікірлерге қосымша ретінде осы ұзақ «массив дыбысталуын» түсіндіруге болады.

Монография жазу барысындағы ережелердің заңдылығы импульстік кернеу әсерінен әлсәіз ортаның бұзылу механизмін зерттеуде Правомерность полученных в монографии положений подтверждается независимыми теоретическими разработками, полученными из других соображений М. Ф. Друкованый, В. М. Комир және В. М. Кузнецовтың тәуелсіз теориялық жұмыстарымен дәлілденеді, бұл жұмыстар [2]-те келтірілген. Онда жалпы бұзылу уақытын, материал көлемінің бірлігін талдау нәтижелері мынадай шешім берді: кернеудің шексіз үлкен шамаға жету кезінде де бұзылу уақыты ақырғы болып қалады, ал кернеу болғанда, уақыт болады. Әрі қарай, осы авторлардың ойынша, нақты денелер тәртібіне (әрекетіне) байланысты болады.

Қолданылған әдебиет

1 Волошин Н. Е. Внезапные выбросы и способы борьбы с ними в угольных шахтах. – Киев: Техника, 1985. – 127 б.

2 Чернов О.И., Пузырев В.Н. Прогноз внезапных выбросов угля и газа. М., Недра, 1979. – 296 б.

3 Липаев Ю.А. О применении метода гидравлических аналогий к решению задач фильтрации газа в угольном пласте / Проблемы рудничной аэрологии. – М.: Недра, 1995. – 287 б.