С.В. Селезнева, И.И. Коновалова

Пензенский государственный технологический университет

МОДЕЛИРОВАНИЕ АЛГОРИТМА ЭКСТРЕМАЛЬНОГО

РЕГУЛЯТОРА ПОДАЧИ ВОЗДУХА В ТОПКУ

Важное место в теории САО занимают алгоритмы импульсных (шаговых) помехозащищенных быстродействующих систем для управления инерционными объектами (энергетическими и химическими установками, ракетными двигателями и т.п.) [1]. Основная проблема при реализации таких алгоритмов в реальном времени заключается в обеспечении устойчивости вычислений решения системы линейных алгебраических уравнений (СЛАУ) при идентификации.

Предлагается решать СЛАУ и усреднять результаты вычислений на основании рекуррентного метода наименьших квадратов (РМНК) [3]. Эффективность предложенного алгоритма оптимизации исследуется методом статистических испытаний.

Рассмотрим модель объекта, которая состоит из последовательно соединенных: экстремального звена (нелинейная часть) с априори неизвестной характеристикой

(1)

звена чистого запаздывания с известной величиной запаздывания τ и линейной части, описываемой разностным уравнением n-го порядка с соответствующими начальными условиями и коэффициентами, зависящими от времени:

(2)

где y(k) – выход модели (временного ряда) в k-й момент времени; e(k) – последовательность независимых, одинаково распределенных случайных величин с нулевым математическим ожиданием и единичной дисперсией (белый шум); {a_i(k), i = 1, n} –параметры авторегрессии; {b_j(k), j=1, m} – параметры скользящего среднего; s – дискретное запаздывание.

Предполагается, что канал измерения выхода объекта, находится под воздействием помехи e(k), которая является центрированным случайным процессом.

Если в k-ый момент времени изменить входную величину модели на , то через некоторое время, определяемое запаздыванием s и временем переходного процесса d на выходе появится отклик . Величину этого отклика можно рассчитать, решив совместно уравнения (1) и (2).

Неизвестные параметры уравнений можно определить, используя рекуррентную процедуру метода наименьших квадратов (РМНК), линеаризуя f(x) в окрестности параметров текущего k-ого шага.

Алгоритм РМНК может быть представлен в следующем виде

, (3)

, (4)

, (5)

где – вектор параметров модели;

- вектор данных;

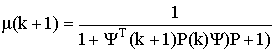– вектор коррекции;

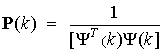– весовая матрица;

– весовая матрица, рассчитанная на следующем шаге; ; – начальные значения переменных.

Алгоритм САО ускоренного поиска экстремума статической характеристики инерционного объекта, в котором используется прогнозирование установившегося значения переходного процесса (2) по измерениям y(k) с использованием рекуррентной процедуры (3 - 5) имеет вид:

(6)

На рисунках 1-3 показаны результаты моделирования алгоритма (6). В процессе моделирования в результате многократного подбора был выбран шаг поиска равный 48, 3 м³/час. Как видно из рисунка использование разработанного алгоритма обеспечивает устойчивую работу системы в области максимальных значений температуры.

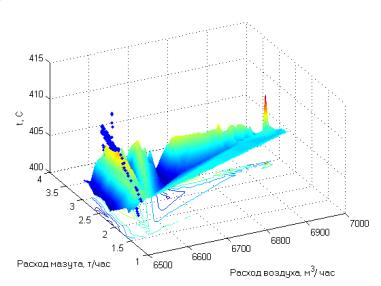
Рис.1. Расчетная зависимость температуры топочных газов от подачи топлива и воздуха

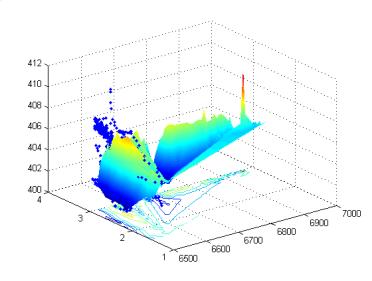
Рис.2. Результат моделирования рекуррентного шагового алгоритма

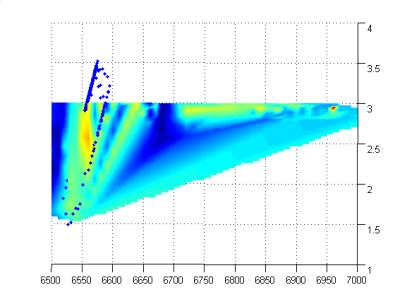
Рис.3. Область поиска глобального экстремума

Список литературы

1. Методы робастного, нейро-нечеткого и адаптивного управления / под ред. Н.Д. Егупова. – М.: Изд – во МГТУ им. Н.Э. Баумана, 2001. -744 с.

2. Л.А. Растригин. Системы экстремального управления. М.: Наука, 1974. – 323 с.

3. Р. Изерман. Цифровые системы управления.- М.: Мир, 1984.- 541 с.