Технические науки/2. Механика

Синчев Б.К. д.т.н. профессор, Муханова А.М. к.т.н. и.о. доцента,

Санаева Г.З. магистрант, Шеметаев А.Б. магистрант

Алматинский Технологический Университет, Казахстан

Моделирование системы управления автоматом

Излагаемый ниже аналитический метод определения положений звеньев механизма Ассура III класса [1] основан на сведении системы векторных уравнений, описывающих независимые замкнутые контуры механизма, к специальной системе векторных уравнений с помощью векторного способа исключения переменных, который опирается на свойства векторов и скалярного произведения. причем число неизвестных в специальной системе  два раза меньше, чем в исходной системе тригонометрических уравнений. Далее специальная система векторных уравнений записывается в декартовой прямоугольной системе координат, т.е. – в скалярной форме. Только затем применяя тригонометрическое тождество sin2j + cos2j  = 1 или универсальную подстановку cos j  = (1- u2) / (1+ u2), sinj = 2u/(1+ u2), переходим к системе квадратных уравнений (число уравнений равно количеству независимых векторных контуров), а не к одному алгебраическому уравнению, как это было сделано у Э. Пейсаха. Установлена связь кратности корня с особым положением механизма. Такова суть предлагаемого метода расчета кинематических параметров, который опубликован в [2].

Данный подход распространен для расчета кинематических параметров системы управления автоматами, основанной на рычажных механизмах.

         Рассмотрим рычажный механизм с трехповодковой группой, представленной на рисунке 1. Векторные уравнения замкнутости механизма III класса с вращательными кинематическими парами имеют вид:

 

                                                                             

                                                                                                                                     (1)

 

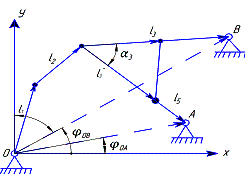
Рисунок 1. – Механизм III класса

         В качестве входного звена можно взять звено 1, а выходного – звено 5. В случае исключения угловых координат  и  мы получим аналогичные уравнения, которые описывали механизм IV класса.

         Последнее означает, что механизм III класса и механизм IV класса имеют два независимых замкнутых векторных контуров. Количество неизвестных данный механизм III класса имеет четыре, т.е. совпадает с количеством неизвестных механизма IV класса.

         Кинематическое исследование механизма III класса полностью совпадает с исследованием механизма IV класса. Следовательно,  разработанный метод определения кинематических параметров механизма IV класса применим к кинематическому анализу механизма III класса.

         Практическую значимость предлагаемого метода покажем на механизме строгального станка, кинематическая схема которого показана на рисунке 2.

 

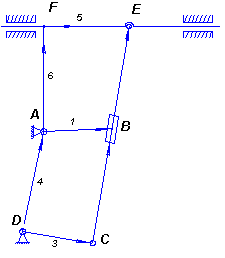
Рисунок 2 –Механизм строгального станка с трехповодковой группой

         Эта схема состоит из двух контуров: ABEFA и ABCDA. В контуре ABEFA имеется следующие переменные: , , , ; в контуре ABCDA- , причем .

         Тогда векторные уравнения механизма III класса, представленного на рисунке 2, равны:       

                  

 

  .

         Эти уравнения в скалярной форме представлены в виде:

,

Уравнения замкнутости для этого же механизма не только с враща­тельными, но и с поступательными кинематическими парами аналогичны с векторной системой (1).

Ставится задача 1: найти положения выходных звеньев группы Ассура III класса при заданных значениях обобщенных координат входных звеньев и размерных параметров:

  

где  

При кинематическом исследовании механизмов высоких классов (МВК) наряду с векторными уравнениями замкнутости необходимо иметь уравнения в проекциях.

Векторные уравнения (1) можно записать скалярной форме:

    

(2)

 

Исключаем угловые координаты  (рис.1)

Используем векторный подход исключения угловых координат из первого уравнения системы векторных уравнений (1) определяем , а из второго -, то есть,

 (3)

.

Далее применяя скалярное произведение,  имеем

Последняя система в более развернутой форме имеет вид:

           После несложных преобразований этой системы для нахождения угловой координаты  получим специальную систему векторных уравнений вида:

 

          

                                                                                                                                     (4)

                             

Приведем (4) к удобной форме:

 

                                                                                                  (5)

                                                                                                      

где 

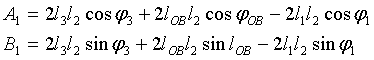
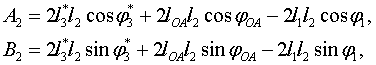
Последняя система (5) эквивалентна системе квадратных уравнений:

 

(6)

                                                                                    

где        

Геометрическая интерпретация уравнений (6) представляет собой кривые второго порядка. Выполнение условий (6) означает, поиск   действительных точек пересечения этих кривых. Общий возможный корень системы (6) равен:

                                                                                                              (7)

где

                     

При этом дискриминанты должны быть больше нуля:

Возможный корень (7) будет общим действительным корнем двух квадратных уравнений, если:

где шаг.

На основе полученных результатов можно сделать следующие выводы:

1)                разработан аналитический метод определения положений выходных звеньев механизма Ассура III класса;

2)                 данный подход применен для кинематического моделирования системы управления строгальным станком;

3)                 рассмотрен модельный пример и проведен вычислительный эксперимент, на основе разработанной программы на языке Delphi.

Литература:

1.   Зиновьев В.А. Курс теории механизмов и машин. –М.: Наука, 1972.-364с

2. Синчев Б.К. Кинематический анализ плоских рычажных механизмов // Доклады НАН РК, №3, 2000.-с 39-44.