Технические науки/2. Механика

К.т.н. Гирнис С.Р., д.т.н. Украинец В.Н., Алигожина Д.А.

Павлодарский государственный университет, Казахстан

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОДЗЕМНЫХ ТРУБОПРОВОДОВ ПРИ ВОЗДЕЙСТВИИ ТРАНСПОРТНЫХ НАГРУЗОК

Используя для исследований модельный подход, представим подземный трубопровод как расположенную в линейно-упругом, однородном и изотропном пространстве (массиве) длинную круговую цилиндрическую тонкостенную оболочку, ось которой совпадает с осью z цилиндрической неподвижной системой координат (r, q, z). Такая модель обычно используется при расчете подземного трубопровода, когда земная поверхность не оказывает существенного влияния на его напряженно-деформированное состояние.

Обозначим радиус срединной поверхности оболочки , а её толщину – . В силу малости толщины оболочки полагаем, что массив контактирует с оболочкой вдоль ее срединной поверхности. Контакт между оболочкой и массивом, полагаем жестким. Физико-механические свойства оболочки и массива характеризуются соответственно следующими постоянными: n₀, n – коэффициенты Пуассона; m₀, m – модули сдвига; r₀, r – плотности. Пусть на внутреннюю поверхность оболочки действует движущаяся с постоянной скоростью с в направлении оси z нагрузка интенсивностью Р (транспортная нагрузка). При этом будем считать, что скорость движения нагрузки меньше скоростей распространения волн сдвига в массиве (дозвуковой случай).

Определим реакцию массива на транспортную нагрузку, используя для описания движения оболочки классические уравнения теории тонких оболочек

(1)

,

где u_0z, u_0q, u_0r – перемещения точек срединной поверхности оболочки; P_z, P_q, P_r – составляющие интенсивности транспортной нагрузки P; – составляющие реакции окружающего оболочку массива (s_rj – компоненты тензора напряжений в массиве, j = z, q, r); – оператор Лапласа.

Для описания движения массива воспользуемся динамическими уравнениями теории упругости в векторной форме

, (2)

где l = 2mn/(1–2n), u – вектор смещения упругой среды.

Так как рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Поэтому удобно перейти к подвижной системе координат , связанной с нагрузкой. Тогда уравнения (1) и (2) соответственно примут вид

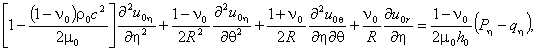
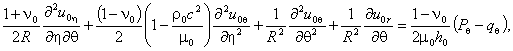(3)

;

. (4)

Здесь – числа Маха; , – скорости распространения волн расширения-сжатия и сдвига в массиве.

Граничные условия при жестком сопряжении оболочки с массивом можно представить в виде

, . (5)

Здесь – компоненты вектора u.

Задача сводится к совместному интегрированию уравнений движения оболочки (3) и массива (4) при выполнении граничных условий (5).

Преобразуем уравнение (4), выразив вектор смещения массива через потенциалы Ламе

, (6)

где – орт оси .

Из (4) и (6) следует, что потенциалы удовлетворяют видоизмененным волновым уравнениям

. (7)

Здесь .

Рассмотрим вначале случай действия на оболочку подвижной синусоидальной нагрузки с произвольной зависимостью от угловой координаты

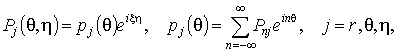(8)

где константа x определяет период T = 2p/x действующей нагрузки.

Потенциалы будем искать в аналогичном (8) виде

. (9)

Выразив компоненты напряженно-деформированного состояния (НДС) массива через потенциалы Ламе можно получить выражения для перемещений и напряжений от синусоидальной нагрузки как функции от .

Подставляя (9) в (7), получим видоизмененные уравнения Гельмгольца

(10)

Здесь ; – двумерный оператор Лапласа.

В дозвуковом случае , и мы приходим к известным решениям уравнений (10)

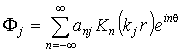, (11)

где – функции Макдональда, ; – неизвестные коэффициенты, подлежащие определению.

В установившемся состоянии зависимость всех величин от имеет вид (8), поэтому для тонкой оболочки

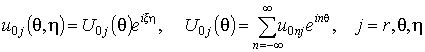. (12)

Подставляя (8) и (12) в (3), для n-го члена разложения получим

(13)

,

где

;

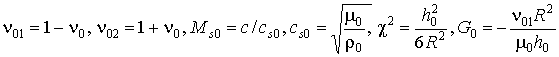при r = R: , , .

Разрешая (13) относительно u_0nh, u_0nq, u_0nr, находим

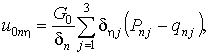
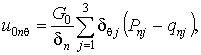(14)

.

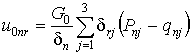Здесь

,

для P_nj и q_nj индекс j = 1 соответствует индексу h, j = 2 – q, j = 3 – r.

Подставляя (11) в ранее полученные выражения для и , получим новые выражения, где неизвестными будут только коэффициенты . Для определения последних воспользуемся граничными условиями (5), переписанными для и с учетом (14). Приравнивая коэффициенты рядов Фурье-Бесселя при e^inq, получим бесконечную систему линейных алгебраических уравнений блочно-диагонального вида для определения коэффициентов a_nj, решение которой находим известным методом, если соответствующий для каждого n определитель системы отличен от нуля.

Зная решение задачи для синусоидальной нагрузки, реакцию массива на движущуюся апериодическую нагрузку характерного для транспортируемых объектов вида P(q,h) = p(q)p(h) формально получаем при помощи суперпозиции, используя представление нагрузки и компонент НДС среды в виде интегралов Фурье:

;

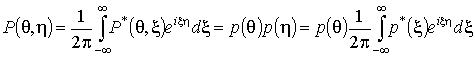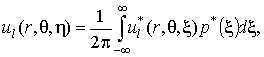
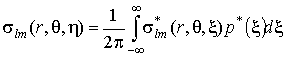. (15)

Здесь , .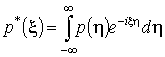

Окончательное решение будет зависеть от конкретного вида движущейся нагрузки.

Для вычисления интегралов (15) можно использовать любой численный метод, если скорость движения нагрузки меньше её критических скоростей, значения которых определяются при исследовании определителей разрешающей системы уравнений. Приравнивая симметричные относительно n и функции к нулю можно получить численными методами дисперсионные кривые в плоскости . Для фиксированного значения n координатам любой точки кривой соответствует свободная волна, распространяющаяся вдоль оси оболочки. Форма этой волны зависит от числа n и удовлетворяет соответствующей однородной системе уравнений. Проведенные численные исследования показали, что в зависимости от физико-механических и геометрических параметров задачи, для каждой n-моды может существовать дозвуковая, соответствующая минимуму построенной в плоскости дисперсионной кривой критическая скорость , при которой в двух точках

.

В этом случае стационарного решения задачи для данной моды не существует. Причём, минимальная критическая скорость, независимо от условия сопряжения оболочки со средой, имеет место при n = 0. Поэтому, если , то для любых и n, и для вычисления интегралов (15) можно воспользоваться численными методами.

При для каждого n существуют четыре особые точки , в которых

.

В этих случаях решение существует, если ранг расширенной матрицы равен рангу матрицы системы уравнений для данной n-моды. При движении с такими сверхкритическими скоростями нагрузка генерирует позади себя свободные цилиндрические незатухающие вдоль оси оболочки гармонические волны частоты и длины , движущиеся вдоль поверхности оболочки вслед за действующей нагрузкой с той же скоростью. Амплитуда этих волн не зависит от z и экспоненциально затухает при .

При точки и сливаются в одну . Стационарного решения задачи в этом случае не существует. Для таких скоростей в оболочке возникают резонансные явления, для изучения которых следует переходить к нестационарной постановке задачи. Значение параметра задачи можно характеризовать как точку бифуркации решения, при переходе через которую возникает неустойчивость движения. Этот факт может оказаться существенным для практики строительства подземных транспортных сооружений.

В качестве примера рассмотрим подземный стальной трубопровод (R = 1м, h₀ = 0,02м; n₀ = 0,3, m₀ = 8,08×10⁴МПа, r₀ = 7,8×10³кг/м³) в массиве известняка (n = 0,25, m = 2,8×10³МПа, r₁ = 2,65×10³кг/м³; c_s = 1028м/с).

На рис. 1 при x > 0 изображены полученные для этого случая дисперсионные кривые с (м/с) ~ x (м^-1). По дисперсионным кривым определены критические скорости транспортной нагрузки: c_(0)* = 952 м/с, c_(1)* = 953 м/с, c_(2)* = 956 м/с, c_(3)* = 971 м/с. Из этого, как было отмечено выше, следует, что минимальное значение критическая скорость имеет место при n = 0. В дальнейшем ограничимся исследованием только этой критической скорости транспортной нагрузки.

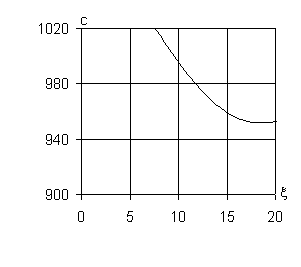
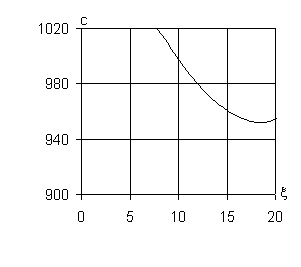
а) n = 0 б) |n| = 1

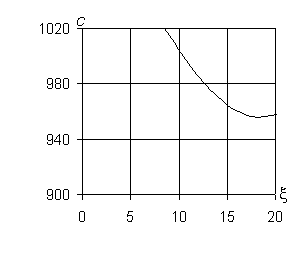
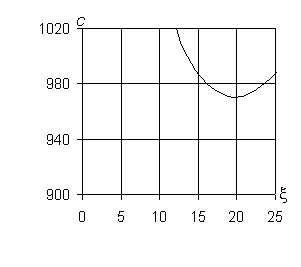
в) |n| = 2 г) |n| = 3

Рис. 1 – Дисперсионные кривые для трубопровода в массиве известняка

При увеличении жесткости породного массива, как показали расчеты, критическая скорость нагрузки c_(0)* возрастает. Например, для алевролита (n = 0,28, m = 4,69×10³МПа, r = 2,7×10³кг/м³; c_s = 1318м/с) – c_(0)* = 1173 м/с, для песчаника (n = 0,28, m = 7,8×10³МПа, r = 2,5×10³кг/м³; c_s = 1766м/с) – c_(0)* = 1470 м/с.

Уменьшение толщины стенки трубы h₀ приводит к понижению критической скорости нагрузки c_(0)* независимо от жесткости породного массива. Так, рассчитанные при h₀ = 0,01м значения c_(0)*, составили: для известняка – c_(0)* = 935 м/с, для алевролита – c_(0)* = 1160 м/с, для песчаника – c_(0)* = 1460 м/с.

Понижение критической скорости нагрузки c_(0)*, при фиксированной толщине h₀, наблюдается и при увеличении радиуса срединной поверхности трубы R. Проведенные расчеты при h₀ = 0,02м и R = 1,5м, показали: для известняка – c_(0)* = 940 м/с, для алевролита – c_(0)* = 1164 м/с, для песчаника – c_(0)* = 1463 м/с. При h₀ = 0,01м и R = 1,5м: для известняка – c_(0)* = 932 м/с, для алевролита – c_(0)* = 1157 м/с, для песчаника – c_(0)* = 1458 м/с.

Как показали расчеты, при одновременном изменении h₀ и R, но постоянном отношении h₀/R, значения критической скорости нагрузки c_(0)* не меняется. При уменьшении h₀/R происходит понижение c_(0)* до определенного значения.