Технічні науки/ 2. Механіка

К.т.н. Врюкало В.В., Гавронський Т.І.

Івано-Франківський національний технічний університет нафти і газу, Україна

Дослідження напруженого стану напівпростору під індентором, який навантажений силою, що направлена під кутом відносно нормалі до напівпростору

В технологіях, які використовуються в багатьох галузях, застосовуються процеси взаємодії жорстких інденторів з поверхнею. Зокрема, така взаємодія має місце в процесах руйнування гірських порід буровим інструментом.

Задача про взаємодію індентора з гірською породою розглядалась багатьма дослідниками. Це, в першу чергу, класична задача Бусінеска [1] про дію концентрованої сили на пружний напівпростір. Численні роботи з теорії пружності розглядають методи розв’язку подібних задач. Стосовно до задач руйнування гірських порід задача про впровадження штампу–індентора теоретично та експериментально розглядалась в роботах Л.А. Шрейнера,
В.С. Владиславлева, Б.В. Байдюка, Р.М. Ейгелеса, Н.Н. Павлової та інших [2-4].

Теоретичні дослідження задачі про впровадження індентора в напівпростір розглядали випадок прикладання сили вздовж осі індентора вздовж нормалі до поверхні. В такій постановці задача була вісесиметричною, що при використанні полярної системи координат дозволяло шукати рішення даної просторової задачі як двовимірної (плоскої).

В реальних умовах роботи породоруйнуючих елементів (зубків) бурового інструменту (долота) напрям прикладання сили через зубок долота проходить не завжди вздовж нормалі до поверхні гірської породи. Тому задачі дослідження характеру взаємодії індентора з напівпростором при різних кутах прикладання сили, і впливу цього кута на напружений стан, що виникає в напівпросторі, є актуальними. У вказаній постановці просторова задача, що розглядається є повністю тривимірною.

Для дослідження впливу напрямку прикладання сили на напружений стан напівпростору допускаємо, що в процесі взаємодії індентора з напівпростором не виникає пластичних деформацій, тобто розглядаємо поведінку гірської породи при її навантаженні в межах пружних деформацій, що є справедливим для твердих та крихких порід. В цьому випадку величина прикладеного зусилля не буде впливати на характер напружено-деформованого стану середовища під індентором.

Дослідження поставленої вище задачі проводилось чисельним моделюванням з використанням методу скінченних елементів (МСЕ) в середовищі пакету ANSYS [5]. Розглядалась взаємодія індентора, виготовленого з твердого сплаву, з твердою гірською породою типу кварцит. Фізико-механічні характеристики матеріалів індентора та напівпростору, утвореного гірською породою, вважались ізотропними. Використовувались наступні значення модулів Юнга (Е) та коефіцієнтів Пуасона (µ):

– для твердого сплаву – Е=5,5∙10¹¹ Па, µ=0,2;

– для кварциту – Е=8,2∙10¹⁰ Па, µ=0,17.

Приймалось, що між поверхнями індентора та напівпростору діють сили тертя з коефіцієнтом тертя k=0,5.

Так як модулі деформації металів є на порядок вищими, ніж модулі деформації гірських порід, то вважалось, що індентор, який вдавлюється в напівпростір, є абсолютно жорстким.

При створенні скінченно-елементної моделі напівпростору його розміри вибирались такими, щоб забезпечити мінімальний вплив бокової границі області, яка була обмежена в радіальному переміщенні, та основи моделі, яка жорстко закріплювалась, на розподіл напружень від дії індентора. Діаметр індентора становив 10 мм. Розрахункова сітка скінченних елементів в зоні концентрації напружень будувалася густішою, ніж на периферії моделі (рисунок 1).

Рисунок 1 – Сітка скінченних елементів на моделі напівпростору

До індентора прикладалась сила F = 1000 Н. Кут між напрямком дії сили та нормаллю до поверхні напівпростору при розрахунках змінювався від 0° до 25°. Отримані результати подані на рисунках 2 і 3. Еквівалентні напруження дозволяють оцінити загальний напружений стан середовища, а нормальні напруження показують характер напружень, що виникають.

Як видно з рисунка 2, зміна кута a прикладання сили не впливає на розмір напруженої зони в глибині напівпростору. Однак, в приповерхневій зоні спостерігається збільшення напружень під індентором на глибині, що дорівнює приблизно 0,25 діаметру індентора.

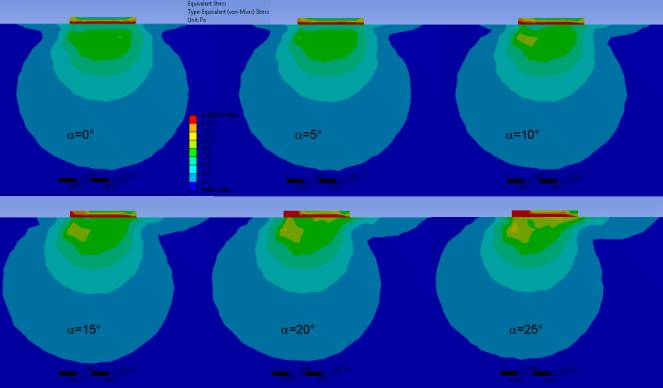
Рисунок 2 – Еквівалентні (за Мізесом) напруження в напівпросторі під індентором в площині дії сили, що направлена під кутом a відносно нормалі до напівпростору в залежності від кута a

Ці напруження зростають за величиною при збільшенні кута a. Також на частині поверхні напівпростору, яка протилежна до напрямку дії сили, виникає напружена зона, розмір якої при збільшенні кута a до величини a=15° зростає, а при подальшому збільшенні кута a залишається практично незмінним. Вказані збільшення напружень будуть сприяти процесу руйнування гірської породи при відповідному направленні сил дії зубка долота на поверхню. Як видно з рисунка 3 збільшення напружень в зоні під індентором досягається за рахунок збільшення стискаючих напружень. А напружена зона на поверхні напівпростору за індентором зумовлена збільшенням розтягуючих напружень. Враховуючи те, що для крихких гірських порід межа міцності на розтяг є на порядок меншою за межу міцності на стиск, зона розтягуючих напружень буде сприяти розвитку тріщин та руйнуванню гірської породи.

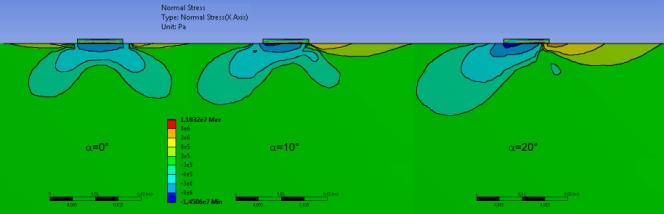
Рисунок 3 - Нормальні напруження в напівпросторі під індентором в площині дії сили, що направлена під кутом a відносно нормалі до напівпростору в залежності від кута a

Таким чином, прикладання сили дії зубка долота під кутом до поверхні гірської породи створює додатковий механізм руйнування цієї породи порівняно з випадком прикладання сили вздовж нормалі до поверхні.

Результати даного дослідження можуть бути використані при конструюванні високоефективного бурового інструменту.

Література

1. Разрушение горных пород при бурении скважин. Спивак А.И., Попов А.Н., 1994. – 264с.

2. Разрушение горных пород при динамическом нагружении. Н.Н. Павлова,
Л.А. Шрейнер – М.: Недра, 1964. – 158 с., ил.

3. Разрушение горных пород при бурении. Р.М. Эйгелес – М.: Недра, 1971.
– 231 с., ил.

4. Механика горных пород. А.И. Спивак, 1967. – 190с., ил.

5. Основы анализа конструкций в ANSYS. А.В.Конюхов – Казань, 2001. – 101с.