Неженцев
А.Б., Гонтарь Д.В.
Восточноукраинский национальный университет им.
В.Даля
Зависимости
нагрузок мостовых кранов от параметров частотного управления
Динамические нагрузки
на металлоконструкцию крана ![]() и груз
и груз ![]() , а также время
разгона
, а также время
разгона ![]() мостового крана
с частотным управлением электроприводов передвижения в значительной мере зависят
от изменения таких факторов как время работы частотного преобразователя (
мостового крана
с частотным управлением электроприводов передвижения в значительной мере зависят
от изменения таких факторов как время работы частотного преобразователя (![]() ), диапазон регулирования частоты напряжения статора (
), диапазон регулирования частоты напряжения статора (![]() ), шаг изменения частоты (
), шаг изменения частоты (![]() ).
).
На примере мостового
крана г/п 10 т, представленного в виде трехмассовой модели, описываемой
нелинейными дифференциальными уравнениями [1] были построены уравнения
регрессии максимальных динамических нагрузок ![]() ,
, ![]() и времени разгона крана
и времени разгона крана ![]() при
частотно-регулируемом пуске [2]:
при
частотно-регулируемом пуске [2]:
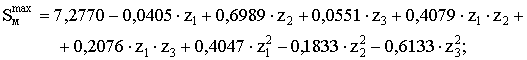 (1)
(1)
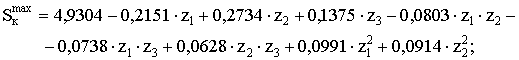 (2)
(2)
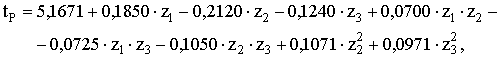 (3)
(3)
где ![]() - кодированные
значения факторов
- кодированные
значения факторов ![]() ,
, ![]() , f1.
, f1.
Для удобства
использования уравнений (1 - 3) в практических расчетах и проведения их
анализа, приведем каждое из них к каноническому виду [3]:
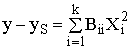 , (4)
, (4)
где ![]() - значение
аппроксимируемого параметра в новом начале координат;
- значение
аппроксимируемого параметра в новом начале координат; ![]() - новые оси
координат, имеющие новый центр и повернутые на определенные углы относительно
старых осей
- новые оси
координат, имеющие новый центр и повернутые на определенные углы относительно
старых осей ![]() ;
; ![]() - коэффициенты при квадратичных
членах уравнения регрессии в каноническом виде.
- коэффициенты при квадратичных
членах уравнения регрессии в каноническом виде.
Для канонического
преобразования уравнения (1) вначале определили координаты условного центра
поверхности отклика ![]() и перенесли начало координат в эту точку. Для этого уравнение (1)
было продифференцировано по переменным
и перенесли начало координат в эту точку. Для этого уравнение (1)
было продифференцировано по переменным ![]() и полученные частные
производные приравняли к нулю. После решения системы трех алгебраических
уравнений были получены координаты нового центра
и полученные частные
производные приравняли к нулю. После решения системы трех алгебраических
уравнений были получены координаты нового центра ![]() :
: ![]() , а также вычислен
главный определитель системы
, а также вычислен
главный определитель системы ![]() . Так как
. Так как ![]() , то поверхность отклика, описываемая уравнением (1),
является центральной, а центр поверхности отклика находится за пределами
области определения факторов.
, то поверхность отклика, описываемая уравнением (1),
является центральной, а центр поверхности отклика находится за пределами
области определения факторов.
Подставив значения ![]() в уравнение (1)
получим прогнозируемое значение параметра
в уравнение (1)
получим прогнозируемое значение параметра ![]() в новом центре поверхности
в новом центре поверхности
![]() . После переноса начала координат в новый центр
. После переноса начала координат в новый центр ![]() уравнение (1) примет
следующий вид:
уравнение (1) примет
следующий вид:
![]() ,
,
где новые координаты ![]() связаны со старыми
связаны со старыми ![]() соотношениями:
соотношениями:
![]() . (5)
. (5)
На втором этапе
преобразования при помощи поворота осей координат освободимся от эффектов
взаимодействия факторов 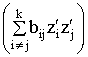 и определим
коэффициенты
и определим
коэффициенты ![]() уравнения (4) в
канонической форме. Для этого найдем корни характеристического полинома
уравнения (4) в
канонической форме. Для этого найдем корни характеристического полинома ![]() матрицы
матрицы ![]() :
:
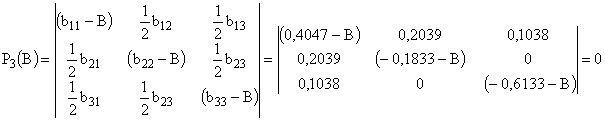 . (6)
. (6)
После соответствующих
преобразований получим полином
![]() , (7)
, (7)
корни которого являются искомыми
коэффициентами ![]() :
:
![]() . (8)
. (8)
Таким образом,
уравнение (1) в канонической форме имеет вид:
![]() (9)
(9)
Аналогично приведены к
каноническому виду уравнения (2) и (3):
![]() (10)
(10)
![]() (11)
(11)
Полученные уравнения
были проанализированы с помощью линий равных откликов в зависимости от ![]() и
и ![]() при
при ![]() (см., например,
рис. 1).
(см., например,
рис. 1).
Связь новых координат ![]() со старыми
со старыми ![]() для двух
факторов
для двух
факторов ![]() осуществляется
с помощью преобразования:
осуществляется
с помощью преобразования:
![]() ; (12)
; (12)
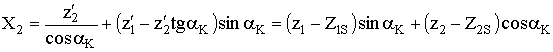 , (13)
, (13)
где угол поворота
координат ![]() определяется из выражения
определяется из выражения
![]() . (14)
. (14)
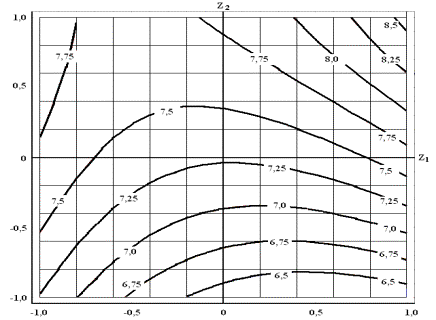
Рис. 1 – Линии равных откликов
динамических нагрузок ![]() при:
при:
z1 = -1…+1
(TP = 2…4 c), z2 = -1…+1 (hЧ = 0,5…2,5 Гц), z3 = 0 (f1 = 42,5 Гц)
Необходимо
подчеркнуть, что рассчитывать максимальные динамические нагрузки ![]() ,
, ![]() и время разгона
и время разгона ![]() с помощью формул (1) – (3), (9) – (11) можно только для рассмотренного
мостового крана с частотным управлением в исследованной области определения
факторов (см. рис. 1).
с помощью формул (1) – (3), (9) – (11) можно только для рассмотренного
мостового крана с частотным управлением в исследованной области определения
факторов (см. рис. 1).
Проведенные исследования позволили сделать
следующие выводы:
- для практического использования весьма
удобны графики линий равных откликов параметров переходного процесса ![]() ,
, ![]() ,
, ![]() при разгоне мостового крана г/п 10 т с частотным управлением. С их
помощью можно не только рассчитывать максимальные динамические нагрузки и время
разгона крана, но и выбирать оптимальные по динамическим нагрузкам и быстродействию
законы частотного управления;
при разгоне мостового крана г/п 10 т с частотным управлением. С их
помощью можно не только рассчитывать максимальные динамические нагрузки и время
разгона крана, но и выбирать оптимальные по динамическим нагрузкам и быстродействию
законы частотного управления;
- увеличение времени работы частотного
преобразователя TP в
период разгона мостового крана приводит к снижению нагрузок ![]() и
и ![]() (до 24%) при незначительном
возрастании времени переходного
процесса tр;
(до 24%) при незначительном
возрастании времени переходного
процесса tр;
- увеличение шага изменения частоты hЧ
приводит к существенному росту нагрузок ![]() и
и ![]() при незначительном
уменьшении времени разгона крана.
при незначительном
уменьшении времени разгона крана.
Литература
1.
Будиков Л.Я., Нгуен
Н.К., Неженцев А.Б. Исследование динамики грузоподъемных кранов // Вестник
машиностроения, №4. - М.: Изд-во Машиностроение, 1981, - С. 39-42.
2. Неженцев А.Б., Аветисян С.М., Гонтарь Д.В. Динамические нагрузки при
передвижении мостовых кранов с частотным управлением // Materiály IХ mezinárodní vědecko - praktická konference «Přední vědecké novinky - 2013». Díl 10. Technickè
vědy. Chemie a chemiská technologie: Praha. Publishing House «Education and
Science» s.r.o, 2013. – s. 24–27.
3.
Неженцев А.Б. Преобразование
и анализ регрессионных моделей при исследовании переходных процессов
грузоподъемных машин // Вісник Східноукраїнського національного університету ім.
В. Даля, № 11 (57). – Луганськ: Вид-во СНУ ім. В. Даля, 2002. – с. 262-269.