Брысина И.В., Макаричева М.А., Макаричев В.А., Макаричев А.В.

Национальный аэрокосмический университет «ХАИ»

Харьковский национальный автомобильно-дорожный университет

ИНТЕНСИВНОСТЬ ВЫХОДА НА УРОВЕНЬ В МНОГОЛИНЕЙНОЙ СИСТЕМЕ МАССОВОГО ОБСЛУЖИВАНИЯ БЕЗ ОЖИДАНИЯ С ГРУППОВЫМ ВХОДНЫМ ПОТОКОМ ЗАЯВОК

В систему массового обслуживания с неограниченным числом приборов обслуживания поступает простейший поток вызывающих моментов с параметром . В каждый такой вызывающий момент возникает одна или несколько заявок на обслуживание, требующих один или несколько обслуживающих приборов по числу возникающих заявок. Вероятность возникновения в вызывающий момент ровно заявок на обслуживание равна (будем называть это требованием - го простейшего потока интенсивности ), . Время обслуживания возникшей в вызывающий момент группы из заявок на таком же количестве приборов одно и то же и представляет собой случайную величину (время обслуживания требования -го потока) с функцией распределения .

Пусть

, , , , .

Предположим, что в начальный момент времени в системе массового обслуживания нет заявок, то есть все каналы свободны (событие ). Обозначим через вероятность того, что в момент в системе обслуживания находятся на обслуживании ровно требований первого потока, ровно требований второго потока,…, ровно требований - го потока, а всего заявок и столько же занято каналов обслуживания при условии (в момент все каналы свободны). Обозначим

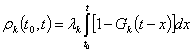и .

Лемма. Для любых целых неотрицательных чисел , для любого справедливо равенство

.

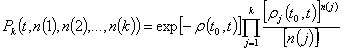Обозначим через число занятых каналов в многоканальной системе без ожидания в стационарном режиме. Переход системы обслуживания из состояния в состояние назовем выходом на уровень ,, или просто выходом на уровень, . Обозначим интенсивность в момент времени этого события – перехода системы обслуживания из состояния в состояние , .

Теорема 1. В момент времени для любого интенсивность выхода на уровень равна

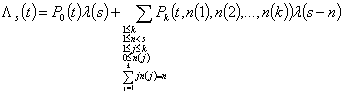, где

.

Теорема 2. Если существуют конечные первые моменты , , то когда

,

.

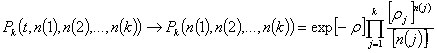Теорема 3. Если существуют конечные первые моменты , , то существует стационарная интенсивность выхода на уровень:

при , где

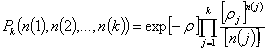и при .

Литература

1. B. V. GNEDENKO AND I. N. KOVALENKO, Introduction to Queueing Theory, Program for Scientific Translations, Jerusalem, 1968.

2. Вопросы математической теории надежности /Е.Ю.

Барзилович, Ю.К. Беляев, В.А. Каштанов, И.Н. Коваленко,

А.Д. Соловьев, И.А. Ушаков; Под ред. Б. В. Гнеденко.- М.:

Радио и связь, 1983.- 376 с., ил.

3. Б.А. Севастьянов. Эргодическая теорема для Марковских

процессов и ее приложения к телефонным системам с

отказами. Теория вероятностей и ее применения, т. 2, вып. 1,

1957, 106-116.

4. А.Н. Ширяев. Вероятность, М.: Наука, 1980, 576 c.

5. R. Fortet. Theorie des probabilities, Centre Nat. Rech. Scient.,

Paris, 1950.