УДК
532:536.24;539.3
Ибраимкулов А.М.,
Божанов Е.Т., Мадалиева С.Н.
(Казахский национальный
исследовательский технический университет имени К.И.Сатпаева Алматы, Республика
Казахстан
Поперечный изгиб
трубчатой конструкции, когда происходить вдавливание жесткого шарика в
поверхность стеклянной пластины.
Постановка задачи
Аннотация. В статье рассмотрена
прочность трубчатой конструкции, когда действует активная критическая сила,
передаваемая через жесткое тело, например, когда происходить вдавливание
жесткого шарика в поверхность стеклянной пластины.
Ключевые
слова: Вдавливание
жесткого шарика в поверхность стеклянной пластины.
Постановка
задачи
1.1.
Решение контактных задач проводится с использованием уточненных теории о
действии через жесткую отпечатку сосредоточенного импульса и реакции основании
типа континуума Коссера. Пусть на тонкую трубчатую конструкцию действует
активная критическая сила 
, передаваемая через жесткое тело, имеющие привязку, что
кривизна кривой изогнутой оси
поверхности контакта, совпадающую с кривизной трубчатой конструкции.
Контактные
усилия для малых областей контакта стремятся прижать трубчатую конструкцию
к жесткой отпечатке. Причем наибольшее
значение они получают в области, близкой к границе отпечатки по Бринеллю.
Усилие на контуре опечатки превышает в
несколько раз усилие, которое возникает в трубчатой конструкции при передаче
через жесткого шарика, не скрепленного с конструкцией. Тогда в рамках принципов
механики конструкции средней толщины математическую модель запишем в виде
[1]-[4].
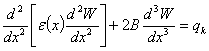(1)
где 
, 
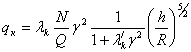(2)
- коэффициент формы поперечного сечения, В- коэффициент континуума Коссера, 
- анизотропные характеристики материала, 
- число полуволн в
продольном направлении, 
- коэффициент формы
нелинейных деформационных процессов, 
- толщина, 
- наименьший радиус
опечатки контактного воздействия.
Общее
решение дифференциального уравнения (1) есть [5]:
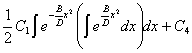(3)
B частности, в первом приближении
+
; 
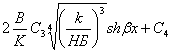(4)
Граничные условия:
, (5)
;
(6)
Подставляя
(4) в (5) и (6) определим произвольные постоянные 
, затем их
значения подставляя в общее решение (4)
получим:
(7)
Здесь 
(8)
(9)
где
(10)
1.2.
Расчет трубчатой конструкции
нагруженного внешним сосредоточенным импульсом, действующего на поперечное
сечение овального площади контакта.
В частности если комплексная податливость
материала конструкции не влияет на коэффициент потери массы континуума Коссера,
то математическая модель (1) будет: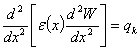 
(11)
при следующих граничных условиях и условиях под
нагрузкой
, 
(12)
; (13)
Частное
решение (11) при граничных условиях (13) и условиях под нагрузкой (12) будет:
(14)
На графиках 1-5 приведены расчеты при следующих
данных
Вычислены из формулы (7)-(10) при следующих
данных график 1
Вычислены из формулы (7)-(10) при следующих
данных график 2
Вычислен из формулы (14) при следующих данных график 3.
;
т.е.
(15)
Вычислен из формулы (14) при следующих данных
график 4.
т.е.
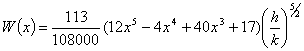(16)
График 5 вычислен из формулы (14) при следующих
данных
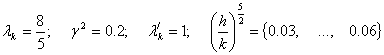т.е.
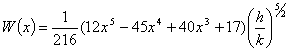(17)
График 1.
Расчет поперечного изгиба конструкции по данным формулы (7)-(10)
График
функций
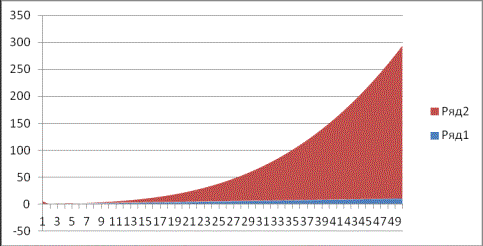
График 2.
Расчет поперечного изгиба конструкции по данным формулы (7)-(10)
График
функций
-
где 
, 
при 
х=(
0,2; 0,4; 0,6; 0,8; 1;
1,2; …; 9;
9,2; 9,4; 9,6;
9,8; 10)
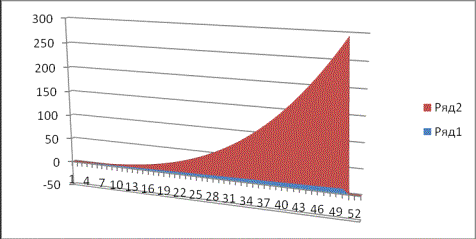
График 3.
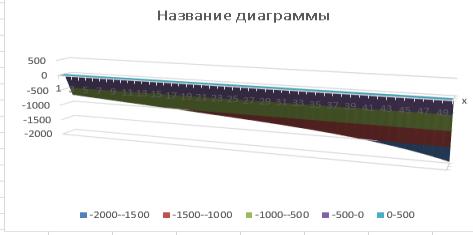
График 4.
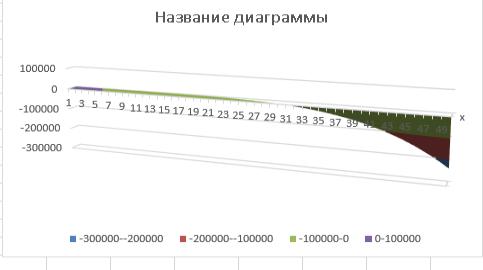
График 5
|
Выводы: |
|
|
Как видно
из графиков №1-2 поперечный изгиб трубчатой конструкции, когда происходит
вдавливание жесткого шарика в поверхность стеклянной пластины связан с
установлением закономерностей упругопластического контакта относительно:
1.
Величин и влияния обратимых форма- изменении опорных поверхностей при
запредельном деформировании разно упрочняющих областей модели Баушенгера и
несвязных сред;
2.
Вязкоупругого сопротивления разноупрочняющих материалов нелинейного деформированного в процесса силового
нагружения;
3.
Возникновения, развития размеров различных контактных зон по Бринелю и
внутренних областей, предусматривающей наличие избыточной энергии значительно
превышающей уровень разрушения.
Как видно из графиков №3-5:
1. Расчёт
на ударную промежуточную вязкость необходимо произвести только на материале с
вдавливанием по середине при условии, что в один конец трубчатой конструкции
скользящие закрепленная.
2.
Наличие у стеклопластиков существенного разно модульного упрочнения может привести к изменению формы отпечатка и
вызвать резкий рость сдвиговой
деформации.
Литература
[1]. Е.Т.
Божанов, Ж.С. Ержанов «Исследование проблем устойчивости упругих тел, гибких
пластик и оболочек и их приложения», Алматы, 2001г., 325 с.
[2].
Божанов Е.Т., Отарбаев Ж.О., Буганова С.Н., «Математическое моделирование
геомеханических процессов», Алматы, 2015г., 145с.
[3].
Додаева А.Н., Божанов Е.Т. Алимжанова Ш.А., Курмангали А. «Об одной
математической модели технологии усадки порошкового материала при неподвиженой
матрице», Вторая международная научно-практическая конференция «Информационные
и телекоммуникационные технологии: образование, наука, практика», Алматы,
2015г., КазНТУ.
[4].
Божанов Е.Т., Ибраиимкулов А.М., Касымбекова М.Т. «Математическая модель
расчета выпучивания тонкостенной многослойной конструкции под действием
ударного импульса, при сдвиговом деформировании площади контакта, когда сила
контактного воздействия сосредоточенная под нагрузкой, а конструкция
закреплена», Mathematics Modern information technologies Physics
Construction and architecture,
Materials of XI international research and
practice conference, volume
8, Sheffield? Science and
education LTD 2015;
[5].
Божанов Е.Т., Ибраиимкулов А.М., Касымбекова М., Абдыгалиева А.К. «Расчет
тонкостенной длинной конструкции под действием ударного импульса, лежащей на
основании типа Коссера…».