МАТЕМАТИКА Прикладная математика.
Мушруб В.А., к.ф.-м.н.,
доцент кафедры экономико-математических методов
Российский экономический
университет им. Г.В. Плеханова;
117997, Российская Федерация, г. Москва, Стремянный пер., 36
Сухорукова И. В., ·д.э.н., профессор кафедры высшей
математики
Российский экономический
университет им. Г.В. Плеханова 117997,
Российская Федерация, г. Москва, Стремянный пер., 36.
Совершенствование методики преподавания теории
опционов.
Активное внедрение современных
информационных технологий в жизни человека привело к развитию инновационных
процессов и в образовании. Современное управление рисками, применяемое в
страховании, торговле на фондовом рынке и инвестировании, основывается на
возможности использовать математические методы для предсказания будущего [4,5].
Конечно, не со 100%-ной вероятностью,
но достаточно точно для того, чтобы принять взвешенное инвестиционное решение.
Основополагающий принцип работы на финансовых рынках состоит в следующем: чем
больший риск вы готовы на себя принять, тем на большее вознаграждение вы вправе
рассчитывать. Использование математики никогда не сможет полностью
элиминировать риск, но может помочь правильно оценить степень принимаемого на
себя риска и решить вопрос о справедливом вознаграждении. При этом значительная
элиминация риска может быть достигнута за счет диверсификации, но для этого
трейдер должен обладать значительным капиталом. В этом смысле торговля
опционами весьма привлекательна: стоимость опциона меньше стоимости базового
актива, а доходность от торговли опционами с некоторой вероятностью может
оказаться весьма высокой. Кроме того, владелец опциона, в отличие от акционера
фирмы, не является ее совладельцем. Этим обусловлена необходимость введения
курса теории опционов для изучения студентами экономических специальностей.
Исследование существенно обновляет и
углубляет методические аспекты преподавания теории опционов. Результаты
исследования могут быть использованы при преподавании и самостоятельном изучении
теории опционов.
Ранее теорию опционов не принято было считать
особо важным разделом теории управления финансами корпораций (в отличие от
теории инвестиций). На самом деле, теория ценообразования опционов используется в оценке стоимости компании так называемым ROV-методом. Некоторые
решения, принимаемые в сфере финансового менеджмента, могут быть лучше
проанализированы и поняты именно в рамках теории опционов. Также теория опционов может быть
использована при анализе прекращения
арендных соглашений или отказа от реализации проектов. Некоторые проекты,
осуществляемые фирмами, предполагают «стратегическую оценку», которая не может
быть обоснована и исчислена в рамках традиционного анализа дисконтированных
денежных потоков. Более достоверная оценка может быть получена с помощью
аппарата теории реальных опционов.
Ядром теории опционов является модель
справедливой цены опциона, разработанная М. Скоулзом и Ф. Блэком.
Рассмотрим опцион Call на одну акцию в качестве
базового актива. Обозначим через ![]() цену акции на момент
исполнения опциона, а через
цену акции на момент
исполнения опциона, а через ![]() цену исполнения
опциона. Напомним, что для опциона колл "в деньгах" (
цену исполнения
опциона. Напомним, что для опциона колл "в деньгах" (![]() ) разность
) разность ![]() между текущей
рыночной ценой базового актива на момент исполнения и ценой исполнения
(страйком) опциона представляет собой доход владельца опциона, заработанный на
основании права покупки базового актика опциона по цене исполнения. Исполнение
же опцион "вне денег" (
между текущей
рыночной ценой базового актива на момент исполнения и ценой исполнения
(страйком) опциона представляет собой доход владельца опциона, заработанный на
основании права покупки базового актика опциона по цене исполнения. Исполнение
же опцион "вне денег" (![]() ) было бы не выгодно для его обладателя, поэтому такой опцион
теряет стоимость. Поэтому стоимость опциона Call на момент его исполнения
выражается в виде усеченной разности:
) было бы не выгодно для его обладателя, поэтому такой опцион
теряет стоимость. Поэтому стоимость опциона Call на момент его исполнения
выражается в виде усеченной разности:
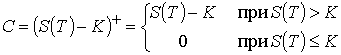 .
.
При покупке опциона уплачивается цена опциона
(премия), теоретическое значение которой устанавливает формула Блэка-Скоулза: ![]() , где
, где 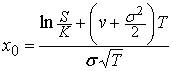 и
и ![]() , где
, где ![]() – годовая безрисковая
ставка непрерывных процентов,
– годовая безрисковая
ставка непрерывных процентов, ![]() – цена исполнения
опциона колл и
– цена исполнения
опциона колл и ![]() – премия за него,
– премия за него, ![]() – современная цена
акции
– современная цена
акции ![]() – ее волатильность.
– ее волатильность.
Отметим, что при любом подходе к
обоснованию формулы Скоулза-Блэка разумно рассматривать вначале опцион Call на
бездивидендную акцию. Как правило, для обоснования обсуждаемой формулы в
учебной литературе применяют модель биномиального блуждания цены акции [1-3].
Несмотря на простоту этой модели, она
является весьма продуктивной. Вместе с тем, обоснование справедливой цены
опциона, основанное на этой модели и изложенное в упомянутых выше учебниках встречается
с определенными трудностями: с одно стороны риск-нейтральные вероятности
выражаются как
![]() и
и ![]() , (1)
, (1)
где ![]() – коэффициент
повышения цены акции,
– коэффициент
повышения цены акции, ![]() – коэффициент
понижения цены акции,
– коэффициент
понижения цены акции, ![]() ,
, ![]() – годовая безрисковая
доходность на данном рынке,
– годовая безрисковая
доходность на данном рынке, ![]() – оставшееся до срока
исполнения время. С другой стороны, та же вероятность
– оставшееся до срока
исполнения время. С другой стороны, та же вероятность ![]() в последующем в
учебнике [2] выражается как
в последующем в
учебнике [2] выражается как 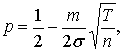 где
где ![]() – волатильность цены
акции,
– волатильность цены
акции, ![]() – ожидаемая
логарифмическая доходность акции. При этом
– ожидаемая
логарифмическая доходность акции. При этом
![]() и
и ![]() , (2)
, (2)
так как это позволяет сделать предельный переход. Подставив значения (2) в (1)
и разложив числитель и знаменатель в ряд Тейлора, получают формулу 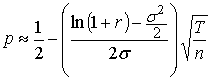 с точностью до
бесконечно малых большего порядка по переменной величине
с точностью до
бесконечно малых большего порядка по переменной величине 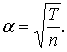 Очевидно, что такое изложение
не является прозрачным для усвоения. Более того, даже для понимания, последней формулы требуется знание
математического ожидания логнормальной случайной величины. Обоснование формулы
Скоулза-Блэка, так же строится на рассуждении подобного типа [3]: для того,
чтобы в пределе переменная величина
Очевидно, что такое изложение
не является прозрачным для усвоения. Более того, даже для понимания, последней формулы требуется знание
математического ожидания логнормальной случайной величины. Обоснование формулы
Скоулза-Блэка, так же строится на рассуждении подобного типа [3]: для того,
чтобы в пределе переменная величина 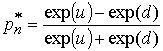 (где
(где ![]() ,
, ![]() ) равнялась
переменной величине
) равнялась
переменной величине ![]() достаточно, чтобы
ожидаемая доходность
достаточно, чтобы
ожидаемая доходность ![]() была равна величине
была равна величине ![]()
Данное изложение довольно сложно для
понимания. Поэтому, нам представляется целесообразным при обосновании формулы
Блэка-Скоулза использовать модель логарифмически нормальных блужданий акции (см
[3]).
В этой модели промежуток времени ![]() разбивается на
разбивается на ![]() отрезков длины
отрезков длины ![]() . Цена акции в момент времени
. Цена акции в момент времени ![]() рассматривается как
случайной величина
рассматривается как
случайной величина ![]() ,
, ![]() . Логарифмы относительных приращений цены
. Логарифмы относительных приращений цены 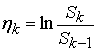 независимы и
распределены по нормальному закону
независимы и
распределены по нормальному закону ![]() . Величина
. Величина ![]() называются логарифмической доходностью
(logarithmical return) за период
называются логарифмической доходностью
(logarithmical return) за период ![]() (см. [2]). Для
освоения студентами этой модели можно решить вместе с ними несколько задач,
приблизительное содержание которых приведено ниже.
(см. [2]). Для
освоения студентами этой модели можно решить вместе с ними несколько задач,
приблизительное содержание которых приведено ниже.
Задача
1. В таблице 1 приведена рыночная
цена акции за 11 торговых дней. Объем выборки – 11 торговых дней.
|
день |
0 |
1 |
2 |
3 |
4 |
5 |
|
цена |
1110.93 |
1078. 1 |
1056. 75 |
1067. 37 |
1046. 23 |
1015. 31 |
|
день |
6 |
7 |
8 |
9 |
10 |
|
|
цена |
1025. 52 |
1035. 82 |
1056. 75 |
1067. 4 |
1088. 93 |
|
Таблица 1
Найдите,
с точностью до сотых логарифмическую доходность акции за период от закрытия
вчера до закрытия сегодня. Ответ приведен в таблице 2.
|
день |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
лог. доходность |
-0.03 |
-0.02 |
0.01 |
-0.02 |
-0.03 |
0.01 |
0.01 |
0.02 |
0.01 |
0.02 |
Таблица 2.
Задача
2.. На основе данных задачи 1 найдите
оценку волатильности. вычислите
однодневные и пятидневные значения стоимости под риском V@R0.99 и
V@R0.95.
Задача
3. Найти математическое ожидание
случайной величины, распределенной логарифмически нормально.
Ответ: 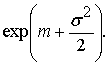
Задача 4. Пусть ![]() – ожидаемая годовая
логарифмическая доходность акции и
– ожидаемая годовая
логарифмическая доходность акции и ![]() – ее волатильность.
Выразите параметры модели α и β2 через
– ее волатильность.
Выразите параметры модели α и β2 через ![]() ,
, ![]() ,
, ![]() и
и ![]()
Задача
5. По какому закону распределена цена
акции ![]() в момент времени
в момент времени ![]() в модели случайного
логарифмически нормального блуждания цены акции? Докажите, что плотность распределения
величины
в модели случайного
логарифмически нормального блуждания цены акции? Докажите, что плотность распределения
величины ![]() имеет
вид:
имеет
вид:
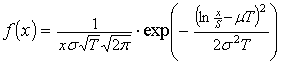 при x>0 и
при x>0 и![]() при
при ![]()
Задача
6. Докажите, что ![]() является модой логнормального
распределения, т. е. докажите неравенство
является модой логнормального
распределения, т. е. докажите неравенство ![]() при
при ![]() .
.
Теперь нужно рассказать о риск-нейтральном
подходе к определению стоимости финансовых инструментов и решить ряд задач, по
тематике изложения.
Предположим, что инвестор сравнивает рисковый и
безрисковый инструменты. Риск-нейтральный подход основан на том, что эти
инструменты признаются эквивалентными, если среднее значение доходности
рискового инструмента совпадает с доходностью безрискового (за тот же период
времени). Нейтральная к риску оценка стоимости финансового инструмента
осуществляется следующим способом. Если в момент времени ![]() найдено
математическое ожидание его стоимости
найдено
математическое ожидание его стоимости ![]() , то современная стоимость равна этому математическому
ожиданию, дисконтированному на безрисковый процент:
, то современная стоимость равна этому математическому
ожиданию, дисконтированному на безрисковый процент:
![]() .
.
Задача 6. Пусть ![]() – ожидаемая годовая
логарифмическая доходность акции. Используя принцип риск-нейтральности,
докажите, что
– ожидаемая годовая
логарифмическая доходность акции. Используя принцип риск-нейтральности,
докажите, что
а) 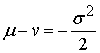 ; б)
; б) ![]() ; в)
; в) 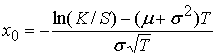 .
.
По принципу риск-нейтральности цена современная
опциона Call равна:
![]() , где f(x) берем из задачи 5. По формуле
математического ожидания НСВ получаем:
, где f(x) берем из задачи 5. По формуле
математического ожидания НСВ получаем: ![]()
![]() =
= ![]()
= ![]()
Поэтому современная стоимость опциона выражается
интегралом
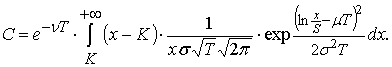
Сделаем замену переменной 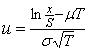 , чтобы перейти к стандартному нормальному распределению:
, чтобы перейти к стандартному нормальному распределению: 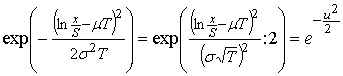 .
.
При такой замене
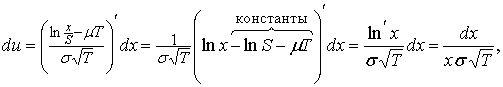 так как
так как ![]() .
.
Следовательно, ![]() Из равенства
Из равенства 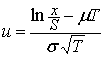 выразим
выразим ![]() и
и ![]() отсюда
отсюда ![]() и
и ![]() Вычисляем
Вычисляем 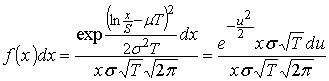 =
= 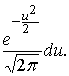
Важно пересчитать предел интегрирования: 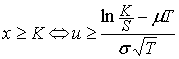 в силу возрастания
функции
в силу возрастания
функции 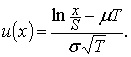 Заметим, что по
задаче 7:
Заметим, что по
задаче 7: 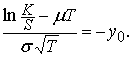
Стоимость опциона представляется в виде разности двух
интегралов:
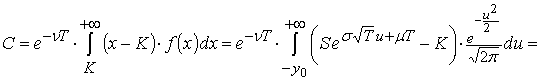
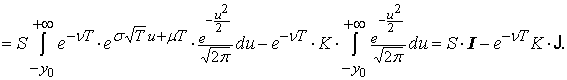
Вычислим эти интегралы по отдельности. Второй интеграл равен 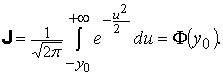 В первом интеграле
сложим все показатели экспоненты
В первом интеграле
сложим все показатели экспоненты  Используем задачу 7 в)
Используем задачу 7 в) 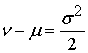 :
:
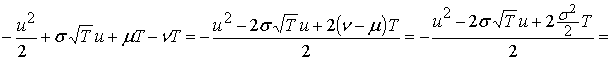
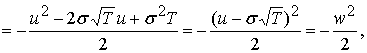 где
где ![]() Заметим, что
Заметим, что ![]() и
и ![]() где
где ![]() Отсюда
Отсюда 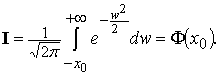 Итак,
Итак, ![]()
В
заключении авторы хотели бы сказать несколько слов о своем опыте преподавании
теории опционов. Преподавание теории опционов студентам управленческих и
экономических специальностей по книге [3] затруднительно, так как требует
специальных математических знаний. Книги [1] и [2] более удобны для этих целей.
И все же авторам пришлось разработать специальную методику преподавания этого
раздела. Методологическим аспектом здесь является включение использование
модели логарифмически нормального блуждания цены акции, которая оказалась
удачной и в плане теоретических рассуждений. Эта модель связана с практическими
задачами, ведь логарифмическая доходность одно из базовых параметров в
практических трейдинговых системах. Кроме того, авторы включили в свой курс
задачи теории вероятностей и параллельное изучение упрощенных методов
вычисления волатильности акции по историческим данным. В методическом плане
авторы пришли к выводу, что в процессе преподавания, значительную часть
теоретических сведений лучше представить в виде задач, разбив доказательство
теорем на несколько такого рода задач. Этот подход, по опыту авторов, обеспечивает
высокий уровень понимания студентами теории данного раздела и приобретение ими
практических навыков и умений.
Литература:
1. Ю.-Д.
Люу. Методы и алгоритмы финансовой математики. – М.: БИНОМ. Лаборатория знаний,
2007.
2. А.А.
Солодовников, В.А. Бабайцев, А.В. Браилов. Математика в экономике. Ч. 3. Теория
вероятностей и математическая статистика. – М.: Финансы и статистика; ИНРФРА-М,
2011.
3. С.В.
Жуленев. Финансовая математика. Введение в классическую теорию. Часть 2. – М.:
Издательство Московского университета, 2012
4. Киселев
А.В., Мушруб В.А. Некоторые аспекты теории линейного программирования. // Международная
торговля и торговая политика. (Вестник РГТЭУ) 2013. № 9-10 (79). С. 159-175.
5. Сухорукова И.В., Лихачев Г.Г. Компьютерное
моделирование и математическое обеспечение экономико-социальных задач. – М.: Экономический
анализ, №5 2003 г., с.60-63