УДК 517 926

Общее нелинейное уравнение второго порядка

Чочиев Т. З.

Южный математический институт ВНЦ РАН и РСО-А.

В работе [1] изучается нелинейное уравнение второго порядка, соответствующее линейному уравнению третьего порядка. В настоящем удалось обобщить это уравнение и применяем к нему тот же способ рассмотрения, что к упомянутому нелинейному уравнению. Устанавливается, что его решение состоит из суперпозиции двух решений: решение линейного уравнения второго порядка и из общего нелинейного уравнения Риккати.

Ключевые слова: уравнение, нелинейное, линейное, выполнимость, удовлетворение, класс Риккати.

П.1. Нелинейное уравнение второго порядка.

Вышеупомянутое общее уравнение имеет вид:

где допускает производную до третьего порядка; и дифференцируемые функции до второго порядка; – непрерывно-дифференцируема, а непрерывная функция; с коэффициентом связан равенством .

С классом уравнений (1.1) связаны решения линейных уравнений третьего порядка[1]. Поэтому его изучение в общем виде имеет определенный смысл.

Докажем теорему.

Теорема 1. Если неизвестные функции удовлетворяют системе равенств,

то уравнение (1.1) допускает следующее представление

причем ,

Чтобы убедиться, в (1.1) коэффициентов заменяем своими левыми значениями из выражения (1.2), тогда после группировки получим (1.3). Напоминаем, что исследование в работе [1] нелинейное уравнение.

является частным случаем (1.1), допускающее представление вида:

Будем следовать методу, примененному в работах [1.2.3].

(1.3) переписываем без правой части

Умножаем его на ,

где ; легко сообразить, что

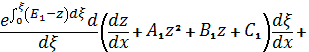
левая часть равенства есть не что иное, как производная произведения,

из которого следует:

где – произвольная постоянная. Или

Но это есть линейное неоднородное уравнение относительно

которое, с целью исследования, переписывается в форме

где

Подобное уравнение нами изучено в [2,4] и его решение зависит от решения нелинейного уравнения класса Риккати [2].

В частности, примем что

где соответственно определяются

Поскольку заданные функции (см. (1.7) и (1.4)), то согласно работам [1,2], можем считать как известные.

Следовательно, с учетом представления

или, после группировки

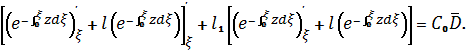
Относительно квадратных скобок имеем линейное неоднородное уравнение первого порядка, из которого

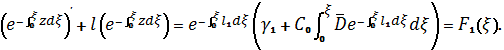
Отсюда для экспоненциальной функции имеем:

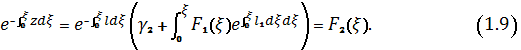
Она и удовлетворяет уравнению (1.7), или уравнению (1.6), установленного из уравнения (1.5). Но уравнение (1.5) получено из (1.3) допущением его правой части

П.2. решение уравнения (1.3).

Вернемся к уравнению (1.3); в переменной – оно допускает представление вида:

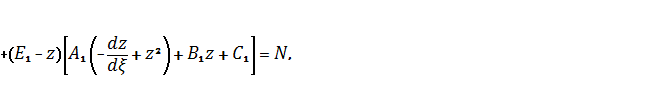
или

Но, поскольку из ,

есть тождество, то произвольную постоянную (согласно идее Лагранжа) заменив функцией

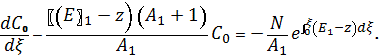
Следовательно

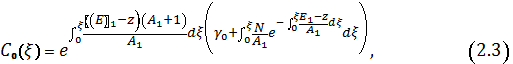
где – постоянная.

Таким образом, (2.2), с учетом (2.3), есть

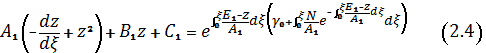
и обращает (2.1) в тождество.

Итак, равенство

есть тоже самое, что и (1.5), или ; но представляет собой (2.2),

которое выполняется тождественно.

Равенство (2.1) есть тоже самое, что и (1.3). Но (2.1) выполняется тождественно если в (2.1) подставить правую часть формулы

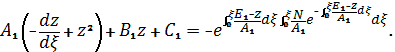
Раз удовлетворяет уравнение (2.1), то и удовлетворяет уравнение (1.3); поскольку в силу (1.4) система равенств (1.2) выполняется, то уравнение (1.1) (1.3) тождественные и из выполнимости (1.3) следует удовлетворение (1.1).

Использованная литература

1. Чочиев Т. З. Дифференциальные уравнения высшего порядка // Основные проблемы естественных и математических наук, II МНК, сборник научных трудов, ИЦРОН, Волгоград, 2015, с. 12-18.

2. Чочиев Т.З. Дифференциальные уравнения высшего порядка. // XΙΙ международная научно – практическая конференция. «Отечественная наука в эпоху изменений постулаты прошлого и теории нового времени» jss 3385-8879 НАУ часть 3. Екатеринбург 2015 г. с. 18 – 24.

3. Чочиев Т. З. Об одном варианте исследования уравнения Риккати // East European Scientific Journal Wschodnioeuropeiskie Czasopismo Naukowe volume 32(2), Polska, с. 61-66.

4. Чочиев Т.З. Об одном варианте исследования уравнения Риккати. // Актуальные проблемы естественных и математических наук в России и за рубежом, международная научно – практическая конференция. Сборник научных трудов по итогам конференции. Новосибирск, 2015. с.10-13.