Калашникова Л.Е., * Рыльцев Е.В.,** Лысак К.Е.***

*Национальный технический университет Украины «КПИ», Киев, Украина.

**Межрегиональная академия управления персоналом, Киев, Украина.

***Художник Национального драматичного Театру им.Л.Украинки, Киев,

Украина.

КООРДИНАТНОЕ ОБЕСПЕЧЕНИЕ ИЗОБРАЖЕНИЯ ОБЪЁМНОГО ОБЪЕКТА НА КАРТИННОЙ ПЛОСКОСТИ ПРИ ПЕРСПЕКТИВНОМ ПРОЕЦИРОВАНИИ

Реферат

Предложена методика вычисления координат точки на картинной плоскости при перспективном проецировании объёмного объекта в процессе построения его изображения в перспективе.

Ключевые слова: количественное значение координат, тримерный объект, перспективная проекция.

Kalashnikov L.E., Ryltsev E.V., Lisak K.E.

*National Technical University of Ukraine "KPI", Department of Biomedical Engineering, Kiev, Ukraine
***Interregional Academy of Personnel Management , Department of advertising,  Kiev, Ukraine
***Аrtist Natsіonalnogo dramatic theater іm.L.Ukraїnki, Kiev, Ukraine

ON THE DEFINITOIN OF THE OBJECT’S COORDINATES ARE PROJECTED ON TO THE PLANE MACHINE PERSPECTIVE PROJECTION

Abstract
The method of calculating the coordinates of the point on the image plane at perspective projection surround the object in the process of building its image in the future.
Key words: quantitative value coordinate trimeric object perspective projection .

При решении задач проективной геометрии возникает, в ряде случаев, необходимость иметь на плоскости («картине») количественное значение координат изображаемого реального тримерного объекта относительно каких-либо иных элементов на «картине» и(или) предметов окружающего пространства, к которому может быть «привязана» и сама «картина». Это важно, в частности, для геодезических, топографических и других проблем. В популярных учебниках [1-5] поднятый вопрос не акцентируется. Это вызывает потребность в его специальном рассмотрения, чему и посвящается настоящее исследование.

В качестве аппарата геометрических преобразований в данной работе используется проецирующий аппарат перспективной проекции [3], из которого основными для нас элементами будут являться: «предметная плоскость» – она же «горизонтальная» плоскость – H, «картинная» плоскость («картина»)–она же «фронтальная» плоскость – V, а также «точка наблюдения» («точка зрения» [3]) – S и наблюдаемый объект – А, проявляющийся в перспективной проекции ввиде точки А¢ на картинной плоскости как точки пересечения «картины» проецирующим лучём (SA) (рис.1–4). В качестве важного элемента проецирующей системы используется здесь также «профильная» плоскость – W [1–5]. Для упрощения процедуры вычислений объект А пpинимался за материальную точку, т.е. за такое пространственное образование, размеры которого бесконечно малы по сравнению с длиной проецирующего луча (SA). Предполагалось в таком случае, что с помощью разработанного здесь аппарата определение координат спроецированных точек протяжённого объекта сведётся к определению координат множества спроецированных точек этого объекта или же координат каких-либо его реперных точек. Исходными данными для решения поставленной задачи являлись известные на проецирующем аппарате координаты точки наблюдения – S и наблюдаемого объекта – А. То есть, величины S_x; S_y; S_z и А_x; А_y; А_z являются заданными. Причём, если координаты точки S и сама эта точка находились в «нейтральном пространстве» [3], т.е. «перед» листом бумаги, на котором изображён рисунок и с которым совпадает картинная плоскость V, то координаты объекта наблюдения А и сам, естественно, объект лежали «за» этим листом , т.е. в «предметном пространстве» [3] (рис.1–4). Все символы и обозначения, используемые в настоящей работе, взяты из [1–5]. Для краткости и упрощения изложения координаты «действующих» элементов рисунка используются здесь в их абсолютном значении независимо от положения этих элементов в координационном пространстве. Отметим также, что каждый рисунок «наполнялся» оптимальным количеством элементов и обозначений, чем преследовалась цель достичь максимальной наглядности изображаемого даже, если эти элементы и обозначения не предполагались быть использованными в обсуждении по ходу исследования. Для облегчения анализа полученых здесь результатов, при их сравнении друг с другом обозначения на рисунках имеют по возможности унитарный характер. Для вычислений использовался математический аппарат из [6;7].

Поставленная задача, а именно, определение координат точки А' на картинной плоскости может быть сформулирована в трёх вариантах, каждый из которых имеет три решения. Один из них реализуется, когда перпендикулярная к плоскости Н плоскость «наблюдения» с лежащим в ней лучём (SA) перпендикулярна «картине». То есть, «смотрим прямо перед собой на картину». Это означает, что S_x=A_x.

Другой вариант имеем, когда «смотрим через картину» на объект А «влево» от ортогонального к «картине» направления, т.е. S_x>A_x (рис.1; 2).

И ещё один – это, когда «смотрим» на объект А «вправо» от той же «ортогональности», т.е. когда A_x>S_x (рис.3; 4).

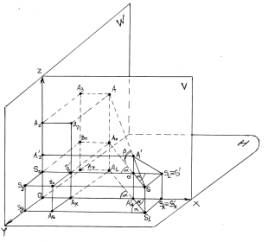
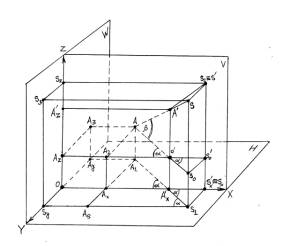
Рис.1. Рис.2.

Рис.1. Проецирующий аппарат перспективного проецировния точки А, наблюдаемой из точки S при условиях S_x > A_x ; S_z > A_z .

Рис.2. Проецирующий аппарат перспективного проецирования точки А,

налюдаемой из точки S при условиях S_x > A_x; S_z < A_z .

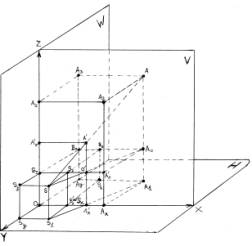
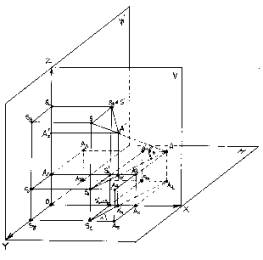
Рис.3. Рис.4.

Рис.3. Проецирующий аппарат перспективного проецирования точки А,

наблюдаемой из точки S при условиях S_x < A_x; S_z > A_z .

Рис.4. Проецирующий аппарат перспективного проецирования точки А,

наблюдаемой из точки S при условиях S_x < A_x; S_z < A_z .

Решение задачи в каждом из указанных вариантов в свою очередь может быть реализовано также в трёх подвариантах. Один из них предполагает наблюдение объекта А «снизу – вверх», т.е., когда S_z<A_z (рис.2; 4). Второй возможен при наблюдении объекта А «сверху–вниз». При этом S_z>A_z (рис.1; 3). Третий - реализуется при S_z=A_z. Во всех вариациях задачи ≡0, поскольку решение этой задачи находится на плоскости («картине»), т.е, в двумерном пространстве, метрика которого задаётся двумя координатами − аппликатой и абсциссой.

Рассмотрим рис.1. Он соответствует условию задачи при S_x>A_x и её подварианту с условием S_z >A_z. Угол «зрения» , т.е., угол, под которым плоскость «наблюдения» SAA₁S₁ пересекает «картинную» плоскость V по линии – это угол a. Поскольку, как видно из рис.1, треугольник Δ=Δ , а взаимно параллельные плоскости этих треугольников перпендикулярны «картинной» плоскости, то Ð=Ð= =Ð=Ð=Ða.

Угол ÐSAS₀=b − это угол между проецирующим лучом (SА) и горизонтом, представленным прямой (АS₀). В таких обозначениях могут быть записаны теперь выражения для абсциссы − и аппликаты − точки A¢ как перспективной проекции точки (объекта) А. А именно, из рис.1 следует: =(OA_x)+(). Ho (OA_x)=A_x, а длина прямой () − одного из катетов Δ− записывается как:() = (A₁A_x)ctga = A_yctga. Из ΔA₁A_sS₁ имeем сtga = (A_sS₁)/(A₁A_s). Катеты этого треугольника − (A_sS₁)=S_x–A_x и (А₁А_s)=S_y+A_y. Cледовательно, ctga=(S_x−A_x )/(S_y+A_y). Тогда = A_x +A_y(S_x−A_x)/(S_y+A_y).

Значение аппликаты точки А' на рис.1 можно записать так:

= (OA_z)+()=A_z+(A¢O¢ ) , где отрезок (А¢О¢) = (AO¢ )tgb.

Из ΔAA₂O’ имеем (АО¢) = (АА₂)/sina = A_y/sina . Таким образом, получаем = A_z + (A_y/sina)tgb . Значение tgb можно определить из ΔSAS₀ .

А именно, tgb = (SS₀)/(AS₀), где (SS₀)=S_z−A_z, а (AS₀) = (AO¢) + (O¢S₀). Если учесть, что (О'S₀)=()/sina , при () = ()=S_y и (O'S₀) = S_y/sina, то (АS₀) = A_y/sina + S_y/sina. Тогда tgb = [(S_z−A_z)/(A_y+S_y)]sina, а (A’O’) = =(A_y/sina)tgb = (A_y/sina)[(S_z−A_z)/(A_y+S_y)]sina = A_y(S_z−A_z)/(A_y+S_y).

Подставляя последнее выражение в уравнение для (см. выше), получим =A_z+A_y(S_z−A_z)/(S_y+A_y). В случае, когда проецирующий луч наблюдения (SA) направлен «снизу – вверх – влево», т.е, когда S_x>A_x при S_z<A_z (рис.2) абсцисса точки A' как функция координат точек S и A определяется тем же соотношением, что и в первом случае (рис.1). А именно (рис.2), =(OA_x)+()=A_x+A_yctga, т.е. =A_x+A_y(S_x-A_x)/(S_y +A_y).

Подобно первому случаю (рис.1) получаем аппликату точки A' и по рис.2. Однако это выражение несколько отлично от предыдущего случая, а именно, = S_z +S_y(A_z − S_z)/(A_y + S_y). Отличие определяется превышением аппликаты точки S над аппликатой точки А и тем, что вершина угла Ðb находится в этом случае в нейтральном пространстве проецирующего аппарата [3] в то время как в случае, представленном на рис.1, она находится в предметном пространстве. Именно от этого зависит вид формулы определения tgb,применяющейся в ходе вычисления величины . Рис.3 соответствует условию стоящей здесь задачи при S_х<A_x и S_z>A_z с вершиной угла Ðb в предметном пространстве проецирующего аппарата [3]. Вычисления проводились по уже использованной здесь схеме при решении задачи в её первом и втором вариантах (рис.1; 2). В варианте, представляемом рис.3, вычисления базировались на свойствах прямоугольных треугольников: ΔSS₀A; ΔA¢O¢A и ΔS₀B₀A. В результате имеем: =S_x+S_y(A_x−S_x)/(S_y+A_y); =A_z+A_y(S_z−A_z)/(S_y+A_y).

И, наконец, рис. 4, который соответствует наблюдению объекта А «направо – вверх», т.е, S_x<A_x и S_z<A_z. Используемые для расчётов прямоугольные треугольники на рис.4 − это ΔASA₀ (ÐASA₀ = β находится вершиной в «нейтральном» пространстве) и подобный ему ΔA’SO’; ΔS_xS₁A₁ = =ΔS₀SA и подобные им Δ=ΔS₂SO’(ÐS₂O^¢S = Ð=a). Основываясь на их свойствах и используя применённый выше способ преобразований исходных данных, можно записать:

= S_x+S_y(A_x − S_x)/(S_y + A_y) и = S_z + S_y(A_z − S_z)/(S_y + A_y).

Полученные выражения без труда преобразуются в формулы для определдения значений , и в случае варианта условия задачи, в котором S_x=A_x. В этом варианте как для случая S_z>A_z , так и для случая S_z<A_z абсцисса точки A' cовпадает с абсциссами точки наблюдения и объекта наблюдения, т.е. º (S_x=A_x). Выражения для апликаты точки A' в этих двух случаях такого варианта условия задачи совпадают с подобными выражениями для вариантов, рассмотренных выше. Применяя приёмы проведенного здесь ранее анализа к соответствующему графическому построению, легко можно получить вариации координат точки А’ и при условии S_z=A_z. А именно, в этом случае при S_x<A_x =S_x+S_y(A_x−S_x)/(S_y+A_y), а при S_x>A_x =S_x−S_y(S_x−A_x)/(S_y+A_y), тогда как в обоих этих вариантах: ≡ (S_z = A_z).

И, наконец, последний вариант координат точки А’ из рассмотренной здесь процедуры перспективного проецирования реализуется при условиях – S_x=A_x и S_z=A_z. В этом случае координаты точки А' на картине выражаются как ≡ (S_x=A_x) и ≡ (S_z =A_z).

Результаты, полученные в настоящей работе, сведены в таблицу.

Таблица. Формулы для вычисления координат точки – перспективной проекции точки А на картинной плоскости. S –точка наблюдения.

Условия задачи		Расчётные формулы
І вариант
Sx>Ax	Sz>Az (рис.1)	=Ax+Ay(Sx–Ax)/(Sy+Ay)
		=Az+Ay(SzAz)/(Sy+Ay)
	Sz<Az (рис.2)	=Ax+Ay(SxAx)/(Sy+Ay)
		=Sz+Sy(AzSz)/(Sy+Ay)
	Sz=Az	=Sx–Sy(SxAx)/(Sy+Ay)
		=Sz
ІІ вариант
Sx<Ax	Sz>Az (рис.3)	=Sx+Sy(AxSx)/(Sy+Ay)
		=Az+Ay(SzAz)/(Sy+Ay)
	Sz<Az (рис.4)	=Sx+Sy(AxSx)/(Sy+Ay)
		=Sz+Sy(AzSz)/(Sy+Ay)
	Sz=Az	=Sx+Sy(AxSx)/(Sy+Ay)
		=Sz
ІІІ вариант
Sx=Ax	Sz>Az	=Sx
		=Az+Ay(SzAz)/(Sy+Ay)
	Sz<Az	=Sx
		=Sz+Sy(AzSz)/(Sy+Ay)
	Sz=Az	=Sx
		=Sz

Литература

1. Чалый А.Т. Курс начертательной геометриию. - Н. М.-К. : МАШГИЗ, 1952.- 279 c.

2.Колотов С.М. Начертательная геометрия. - К.: «Вища школа», 1975. - 261 с.

3. Виноградов Н.Н. Начертательная геометрия. - Минск: «Высшая школа», 1977.- 368 с.

4. Фролов С.А. Начертательная геометрия. - М,: МАШИНОСТРОЕНИЕ», 1978, - 240 с.

5. Михайленко В.Є., Євстіфеєв М.Ф., Ковальов С.М. Нарисна геометрія. - К.: «Вища школа», 2004. - 300 с.

6. Нікулін О.В. Геометриія. Поглибленний курс.- К.: «ПЕРУН», 1999.- 349с.

7. Жолдак М.І., Грохольська А.В., Жильцов О.Б. Математика (тригонометрія, геометрія, елементи стохастики). - К.: МАУП, 2004. - 456 с.