Технические науки / металлургия

Ревун М.П., Зінченко В.Ю., Іванов В.І., Чепрасов О.І., Мосейко Ю.В.

Запорізька державна інженерна академія

РОЗРОБКА МАТЕМАТИЧНОЇ МОДЕЛІ НАГРІВАННЯ ЗЛИТКІВ У ПОЛУМЕНЕВИХ ТЕРМІЧНИХ ПЕЧАХ КАМЕРНОГО ТИПУ

У роботі [1] виконано аналіз існуючих математичних моделей нагрівання злитків щодо полуменевих термічних печей камерного типу.

Необхідною є розробка математичної моделі нагрівання злитків, що дозволить без вирішення диференціальних рівнянь теплопровідності складати алгоритм змінювання температури гріючого середовища за часом для забезпечення заданого розподілу температури щодо перерізу металу.

Розглядають одномірну задачу нагрівання злитку товщиною з постійними коефіцієнтом теплопровідності , питомою теплоємністю і щільністю металу :

, (1)

; (3)

; (4)

, (5)

де , – поточні значення температури гріючого середовища та поверхні злитку, °С, відповідно; – коефіцієнт температуропровідності металу, м²/с, якого визначають з використанням співвідношення для середніх значень наведених параметрів; – функція розподілу температури у злитку за координатою на початковий момент часу.

Вирішення рівняння теплопровідності (2) з крайовими умовами (3)-(5) виконують методом кінцевих різниць [3].

Залежність температури поверхні злитку від температури гріючого середовища оцінюють за допомогою співвідношення:

, (6)

де , – сумарний коефіцієнт тепловіддачі, Вт/(м×К), знак « ± » означає процес нагрівання або охолодження злитку, відповідно.

Рівняння (1), (3.) і (6) описують математичну модель, що дозволяє обчислювати поточні значення показників якості нагрівання металу, проте залишаються проблеми щодо визначання коефіцієнта , необхідного для розрахунків критерію .

Виходячи з того, що кожному розподілу температури у металі відповідає певне середньо масове значення температури , можна записати

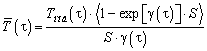. (7)

З іншого боку, розглядаючи процес нагрівання металу як акумуляцію теплоти відповідно до рівняння [4]

, (8)

де , – коефіцієнти форми та масивності тіла, відповідно, – й позначаючи постійну часу нагрівання як можна подати температуру як вирішення рівняння (8) за початкової температури :

. (9)

Прирівнюючи праві частини рівнянь (7) і (9), отримують залежність, яка встановлює взаємозв’язок між параметрами і та дією , що управляє, за часом, тобто оптимізаційну математичну модель у вигляді.

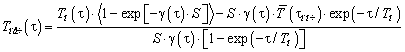. (10)

Відомо, що оптимальне за швидкодії управління є кусочно-постійною функцією часу, а температура гріючого середовища змінюється від гранично-межового значення до величини, яка відповідає заданому рівню температури поверхні злитку. Тому розробку алгоритму управління призводять до визначення моментів переключення теплового навантаження печі, які обчислюють за допомогою формули

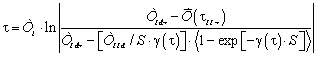. (11)

Як початкові дані для моделювання задають температуру печі, теплофізичні параметри садки злитків, обмеження за швидкістю їх нагрівання, початковий і кінцевий розподіл температури за перерізом металу та .

Використовуючи результати розрахунків, визначають температурно-часовий режим, за дії якого забезпечують заданий розподіл температури у злитку впродовж мінімального проміжку часу: .

Література:

1. Ревун, М. П. К моделированию нагрева металла в пламенных печах камерного типа [Текст] / М. П. Ревун, В. Ю. Зинченко, В. И. Иванов // Наука в інформаційному просторі : матеріали XI Міжнар. науково-практичн. конф. – Дніпропетровськ : видавець Біла К. О. 2015. – Т. 2. – С. 25-28.

2. Коздоба, Л. А. Методы решения нелинейных задач теплопроводности [Текст] / Л. А. Коздоба. – М. : Наука, 1975. – 227 с.

3. Ревун, М. П. Автоматическое управление нагревом металла [Текст] / М. П. Ревун, В. И. Гранковский. – Киев : Техника, 1973. – 319 с.

4. Бутковский, А. Г. Теория оптимального управления системами с распределенными параметрами [Текст] / А. Г. Бутковский. – М. : Наука, 1965. – 476 с.