К.т.т. Данилова Л.Н., Казарян Г.А.

Національний технічний університет України «Київський

політехнічний інститут», Україна

розрахунок параметрів гвинтових поверхонь на деталях машин невеликого розміру

В машинобудуванні широко використовують деталі і інструменти, що мають гвинтові поверхні. В багатьох випадках високі вимоги по точності вимагаються не тільки до діаметру і кроку гвинтової поверхні, але і до її профілю. В залежності від кута підйому гвинтової лінії w, гвинтові поверхні розділяються на різьби і гвинтові канавки. Збільшення кута w викликає зміну перетину, в якому задається профіль гвинтової поверхні, для різьби це осьовий перетин, для гвинтових канавок регламентують торцевий перетин.

Гвинтові канавки, на відміну від різьби, практично не оброблюють точінням, при великих кутах підйому витка кінематичний задній кут на одній із сторін профілю в межах 2⁰ - 4⁰ забезпечити неможливо. Основним методом оброблення гвинтових канавок є метод безцентроїдного обгинання, тобто формоутворення відбувається із застосуванням фасонного інструмента – фрези або шліфувального круга. При цьому профіль поверхні інструмента не співпадає з профілем гвинтової поверхні в жодному перетині, перпендикулярному до осі інструмента.

Вирішення як прямої так і зворотної задач представляє інтерес при проектуванні інструментів, деталей і розрахунках прогнозованої точності оброблення. Оброблення відбувається в умовах підрізання, оброблений профіль деталі залежить від профілю інструмента, його діаметру і від параметрів його установлення, тому задача профілювання має свою специфіку і її треба вирішувати для конкретних умов. Винаходження профілю гвинтової канавки на дрібних деталях машин, що оброблюються інструментом простого профілю, або стандартним інструментом великого діаметру можливо на основі вирішення задачі визначення вихідної інструментальної поверхні при гвинтовому русі циліндричної поверхні деталі відносно поверхні інструмента.

З циліндричною поверхнею інструмента зв'яжемо нерозривно систему координат xyz, а з деталлю – x₁y₁z₁ (рис.1). У процесі гвинтового руху поверхні І щодо поверхні Д система координат xyz буде обертатися навколо осі x₁ системи координат x₁y₁z₁ і рухатися поступально уздовж цієї осі. Позначимо кут повороту через q. Тоді поступальне переміщення буде hq. Формули перетворення координат для цього випадку запишуться в такий спосіб:

x₁ = x cos e – y sin e + hq

z₁ = z cos q + (x sin e + y cos e) sin q

y₁ = (x sin e + y cos e) cos q – z sin q.

У системі координат x₀y₀z₀ точки контакту визначаються рішенням двох систем рівнянь:

1) рівняння поверхні деталі z = f(y);

2) рівняння контакту x = – tg y(z сtge - h) – y₀ сtge;

Спільне рішення цих рівнянь з формулами переходу, тобто система п'яти рівнянь, дає шукану гвинтову інструментальну поверхню, параметр якої дорівнює параметру початкового гвинтового руху.

Практично визначення профілю осьового перерізу поверхні при y₁ = 0 можна робити в наступній послідовності:

1) Вибирають y₀ і обчислюють z₀ по рівнянню z₀ = f(y₀), тобто на профілі фрези обирають ряд точок з координатами y₀ і z₀ . Визначають кут нахилу дотичних в цих точках y до осі у.

2) Для обраних точок по рівнянню контакту визначають x₀;

3) По формулі x₁ = x₀ cos e – y₀ sin e + hq

Для x₁ = 0 визначають кут q для кожної точки профілю.

Де h – це параметр гвинтового руху.

Гвинтовий рух профілю характеризується осьовим кроком Н і кутом нахилу гвинтової лінії поверхні на циліндрі радіусу r або, гвинтовим параметром h. Між цими параметрами існує залежність h = H/2p = r/tg w.

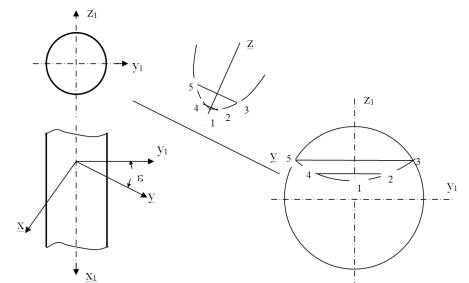
Рисунок 1 – Визначення профілю торцевого перерізу гвинтової поверхні.

4) По формулах перетворення координат

z₁ = z₀ cos q + (x₀ sin e + y₀ cos e) sin q

y₁ = (x₀ sin e + y₀ cos e) cos q – z₀ sin q.

визначають відповідну точку торцевого перерізу поверхні деталі, тобто координати z₁ і y_1.

Розроблене програмне забезпечення дозволяє розрахувати точки гвинтової канавки деталі, що оброблюється інструментом великого діаметру з будь яким профілем (рис.2).

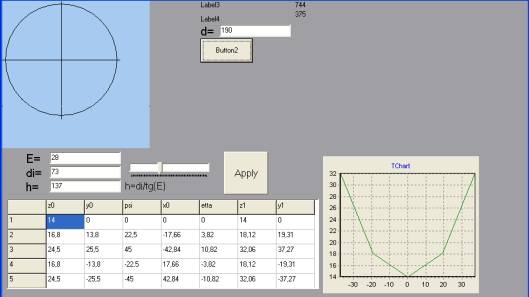
Рисунок 2 – Приклад визначення профілю гвинтової поверхні.