К.т.н, доцент Айнагулова А.С., магистрант Оразова А.А.

Евразийский национальный университет имени Л.Н. Гумилева, Казахстан

Сложные динамические системы (космические объекты) и построение наблюдателя для искусственного спутника Земли (ИСЗ)

В данной работе рассматривается сложные динамические системы, модель углового движения искусственного спутника Земли (ИСЗ) и построение наблюдателя для искусственного спутника Земли (ИСЗ) в классе однопараметрического структурно-устойчивого отображения. Как космический объект можно рассматривать космического летательного аппарата (КЛА). Космический летательный аппарат предназначен для полёта в космос или в космосе, например ракеты-носители (космические ракеты), искусственные спутники Земли (ИСЗ) и др. небесных тел. Также космический летательный аппарат относятся к сложным динамическим системам. Сложной системой (СС) называется система, включающая большое число взаимодействующих элементов (подсистем) и обеспечивающая решение достаточно сложной (комплексной) задачи. К таким системам относятся информационные сети (телефонные, локальные, Интернет), транспортные сети, производственные процессы, системы управления сложными (многоканальными, нелинейными, неопределенными) динамическими объектами (например, воздушными и космическими объектами).

Рассмотрим упрощенную модель углового движения искусственного спутника Земли (ИСЗ) относительно продольной оси, рис.1.1.

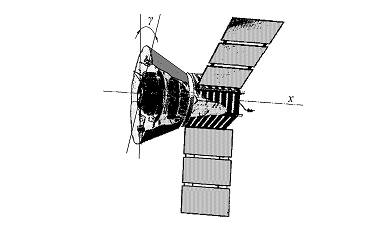
Рисунок 1.1 Искусственный спутник Земли

Обозначим через - угол и угловую скорость крена ИСЗ; - момент инерции ИСЗ относительно продольной оси x; - управляющий момент относительно этой оси, развиваемый, например, реактивными двигателями. Уравнение динамики вращательного движения и кинематическое соотношение, связывающее угол и угловую скорость будет иметь вид:

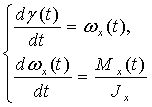(1.1)

Для данной системы n = 2, m = 1. Вектор состояния определяется сопоставлением компонентов значений угла и угловой скорости: 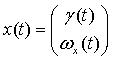. А матрицы векторов состояния и управления будут иметь следующий вид соответственно:

.

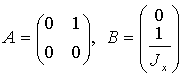Вид матрицы С определяется тем, какие переменные измеряются или относительно каких из них формулируется цель управления. Если измеряется только угол крена, то l = 1 и . Если измеряются обе переменные, то l = 2, .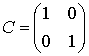

Рассмотрим случай, когда l = 1. Введя переменные , уравнение (1.1) можно записать в виде

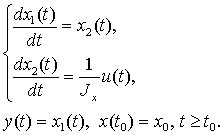(1.2)

Запишем систему (1.2) следующим образом

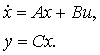(1.3)

Для системы (1.3) наблюдатель будет описываться следующим уравнением

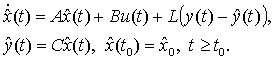(1.4)

Матрицу L выберем в виде

где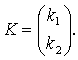

Исследуем работу наблюдателя рассматривая ошибку оценивания . Для этого вычтем из (1.3) уравнение (1.4), учитывая введенную матрицу L . Тогда получим следующее уравнение для ошибки

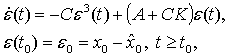(1.5)

где источниками ошибки ε(t) является начальное рассогласование .

Исследуем поведение процесса ε(t). Система (1.5) обладает следующими стационарными состояниями:

(1.6)

(1.7)

Систему (1.5) запишем в развернутой форме

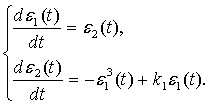(1.8)

Линеаризуем систему (1.8)

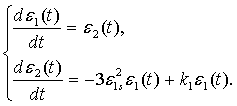(1.9)

При стационарном состоянии (1.6) система (1.9) примет вид:

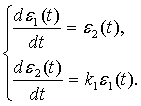(1.10)

Находим характеристическое уравнение системы (1.10)

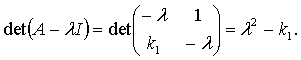
Отсюда следует, что условием устойчивости системы (1.9) является условие .

Рассмотрим устойчивость системы для других стационарных состояний. Тогда при стационарных состояниях (1.7) система (1.9) будет иметь вид:

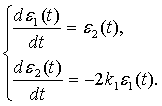(1.11)

Характеристическим уравнением системы (1.11) будет следующее уравнение

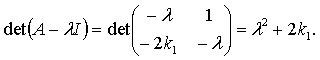
Следовательно, система (1.11) будет устойчива при .

Из полученных условий ясно, что система (1.8) становится устойчивой как при отрицательном, так и при положительном k₁.

Результаты численного эксперимента при различных значениях k₁ и сравнительный анализ при выборе матрицы L, когда ошибка оценивания изменяется по линейному закону, т.е. когда система (1.5) имеет вид:

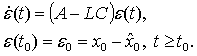(1.12)

Численные эксперименты реализованы с помощью программного комплекса Matlab.

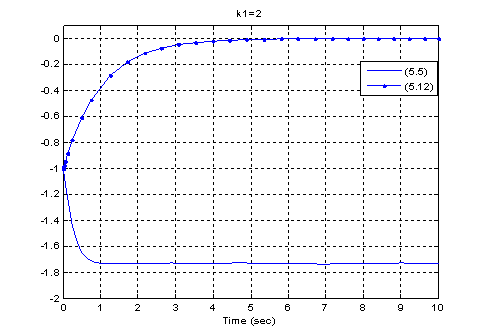
Рисунок 1.2

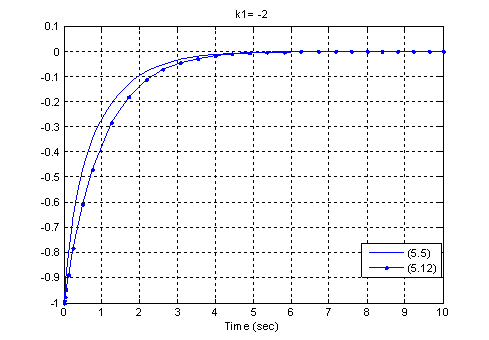
Рисунок 1.3

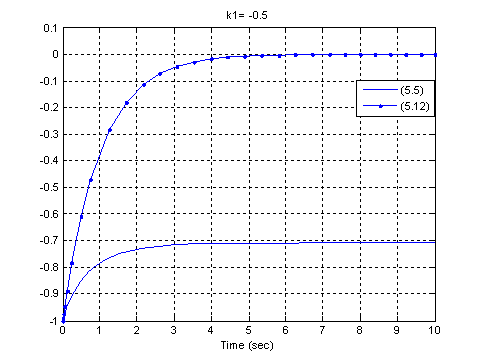
Рисунок 1.4

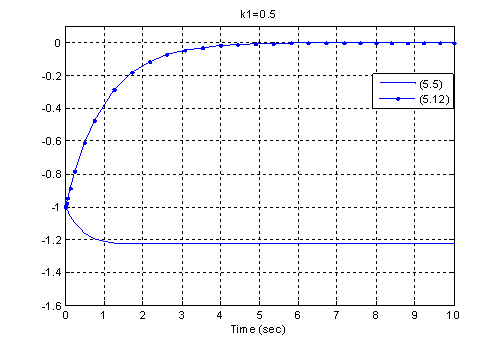
Рисунок 1.5

Литература:

1. Боднер В. А. Системы управления летательными аппаратами. М.: Машиностроение, 1973.502 с.

2. Бейсенби М.А., Айнагулова А.С. Оценка переменных состояний и построение робастно устойчивых наблюдателей в классе структурно-устойчивых отображений // Вестник ЕНУ им. Л.Н.Гумилева. Серия математика, информатика и механика. – 2008. - №4. – Б. 14-27.

3. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 1975. – 768 с.

4. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1986. – 256 с.