Современные информационные технологии

2. Вычислительная техника и прпограмирование

К.т.н. Красиленко В.Г., к.т.н. Дубчак В.М., Вдовиченко Т. В.

Вінницький державний аграрний університет

Дослідження зв’язків між операціями еквівалентністної алгебри та операціями предикатної алгебри вибору.

Останні тридцять років ознаменувались тим, що поряд з традиційними методами цифрової обробки інформації більшу увагу стали приділяти новим методам, математичним апаратом в яких є неперервна, бескінечнозначна, нейронна чи нечітка логіка. Це обумовлено перспективами використання неперервної логіки, її узагальнень, модифікацій, як математичної моделі для гібридних пристроїв збору, обробки, перетворення інформації; нейромережевих інтелектуальних пристроїв розпізнавання, прогнозування; експертних систем, тощо. Математичною основою дискретних та неперервних логік є теорія множин та алгебр. Алгебра, що є одним з основних понять сучасної математики визначається як множина з заданою на ній системою операцій. Розширенням класичної двозначної та k-значної логіки є неперервна логіка (НЛ) та пов’язані з нею алгебри НЛ, в тому числі алгебра Кліні [1] і її неперервно-логічні функції. Існує також низка нечітких та нейро-нечітких логік та асоційованих з ними алгебр [1,2]. Першим найбільш природним узагальненням НЛ є порядкова логіка, в якій на множині вводиться нова базова n-місна операція, що ставить у відповідність довільному набору , де , його r-ний по порядку зростання елемент

Корисні узагальнення НЛ дає гібридна (неперервно-дискретна) логіка, в якій базовими є порогові та депорогові операції [2]:

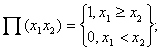
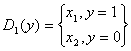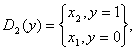, де , а - пороговий оператор, - депороговий оператор.

Одним з цікавих узагальнень НЛ є керована НЛ (по термінології автора, предикатна алгебра вибору (ПАВ) [3]), в якій разом з операцією заперечення вводяться дві узагальнені (керовані) операції : предикатні диз’юнкція та кон’юнкція :

де

- звичайні операції множення та додавання , - m – місний двозначний предикат , а - його заперечення.

Поряд з цим за останні десять років з’явилась низка робіт, що пов’язані з моделями нейромережевої «еквівалентністної парадигми» та відповідними еквівалентністними алгебрами (ЭА) [4-6]. Зв’язки деяких ЭА з відомими функціями скалярного добутку та іншими були вказані ще в роботі [4], сімейство (родина) узагальнених скалярних операцій нейробіологіки еквівалентність (нееквівалентність) на основі узагальнених нечітких t-норм та s-норм [7] було розглянуто в [5], а в [6,8] показані перспективи застосування ЭА, операцій нормованої еквівалентності та моделей на їх основі для моделювання чи створення покращених нейромережевих систем .

Важливе практичне значення має проблема повноти в НЛ, яка аналогічна відповідній в дискретних логіках. Система функцій НЛ називається повною (базисом) в класі R, якщо нову функцію з класу R можливо представити суперпозицією функцій . Відносно прості питання повноти системи функцій НЛ та викладені в багатьох роботах, в тому числі і в [2]. Повнота інших систем може бути визначена на основі результатів встановлення їх зв’язку з функціями вищезгаданих систем. Для цього достатньо виразити кожну функцію відомої повної системи у вигляді формул через функції нової системи.

Тому метою цієї роботи є дослідження зв’язків між операціями еквівалентністної алгебри та операціями предикатної алгебри вибору.

Результати.

По-перше, виразимо еквівалентність () та нееквівалентність типу () через предикатні диз’юнкцію та кон’юнкцію :

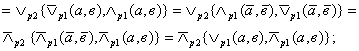
НЕК

Де де - одинична функція.

По-друге виразимо еквівалентність ЕКта нееквівалентність НЕКтипу () , () через та :

НЕК

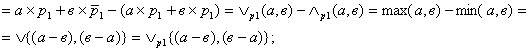
ЕК

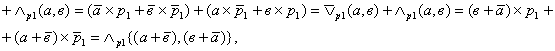
Де

По-третє, оскільки операцію заперечення (-) в предикатній алгебрі вибору (ПАВ) можна реалізувати як: а в ЕК як: , де можуть бути використані операції НЕК та ЕК любого типу:() чи (), та крім того,

то приходимо до наступного.

Для висновку про повноту наступних систем: і асоційованих алгебр ЭА, потрібно виразити через операції НЕК чи ЕК операцію max або операцію min. З іншої сторони (в роботах [2,5]) було показано, що всі операції функції НЛ , тобто: max ,min,, виражаються через примітивно-рекурсивну функцію обмеженої різниці ОБР, тому

система {ОБР,1} є функціональною повною в алгебрі Кліні. А це означає, що з іншої сторони для повноти системи {НЕК,1} треба операцію ОБР виразити через НЕК .

Таким чином, нами досліджені зв’язки між операціями ЭА та ПАВ і поставлені, точно сформульовані задачі для подальших досліджень повноти системи на основі еквівалентністної парадигми.

Література:

1. Шимбирэв П.Н. Гибридные непрерывно-логические устройства – М.: энергоатамизм, 1990-174с.

2. Левин В.П. Непрерывная логика. Ее обобщение и применение. АИТ, 1990, №8,с.3-22.

3. Волгин Л.И. Предикатная алгебра выбора и ее модификации – Таллин-:Валгус, 1986,с. 64-104с.

4. Krasilenko V.G. et al., “Continuous logic equivalental models of Hamming neucal networked architectures with adaptive correlated weighting”, Proc.SPIE,vol.3402,p.398-408,1994.

5. Krasilenko V.G. et al., “The family of neuro-fuzzy logic,their optolectronic realization and applications” , Proc. SPIE, vol.4732, p.106-120, 2002.

6. Krasilenko V.G. et al., “Optical pattern recognition algorithms based on neun- logic equivalental models and demonstration of their prospectiveness and possible implementa”, Proc.SPIE,vol.4387,p.247-260,2001.

7. Кузьмин В.Б. , Травкин С.Н. Теория нечетких множеств. Обзор АИТ, 1992, №11, С. 3-36.

8. Красиленко В.Г. та інші. Деякі новітні результати та досягнення вітчизняної нейроінформатики, Збірник наукових праць, № 8, -НТК, Хмельницький , ВОТТП, с.320-324,2001.