Математика/1. Дифференциальные и интегральные уравнения

д.ф.-м.н., проф. Кусаинова Л.К., докторант PhD, к.ф.-м.н. Оспанова А.Б.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

О сходимости одной разностной схемы для

сингулярной задачи Коши

В данной работе рассматривается одна модель приближенной схемы (разностной схемы) для численного решения задачи Коши дифференциального уравнения первого порядка с сингулярностью на бесконечности. Исследуются вопросы аппроксимации и сходимости на решениях одной приближенной схемы для сингулярной задачи Коши

(1)

где – непрерывная на оси функция, поведение которой на бесконечности задается условиями

Известно, что задача (1) при этих условиях однозначно разрешима для произвольной непрерывной правой части. См. [1].

Пусть () – пространство раз непрерывно дифференцируемых в функций таких, что

Положим . Через будем обозначать пополнение линейного многообразия

по норме

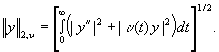
Задачу (1) мы исследуем в операторной форме как

(2)

где оператор

(3)

рассматривается как оператор, действующий из в , где , . Для пары норма

Для построения приближенной схемы (см. [2])

задачи (2), (3) рассмотрим вначале специальный оператор дискретизации , где – пространство сходящихся к нулю числовых последовательностей . Норма в

Зададим характеристический размер Отелбаева относительно функции , полагая

Известно, что

См. [3]. Поскольку , то

Пусть: ,

Положим (). Пусть , – целые такие, что

Обозначим через равномерную сетку на :

Пусть , . Положим

Будем говорить, что удовлетворяет условию медленного изменения относительно своего характеристического размера, если существует такое , что

() как только .

Утверждение. Пусть удовлетворяет условию (). Тогда для любой функции справедлива оценка

где не зависят от .

Введем обозначения. Пусть , , () – пространства векторов , , наделенные нормами:

Здесь () – () -мерное арифметическое пространство. На -ом шаге мы будем рассматривать приближающий оператор

определенный через равенства

где:

Пространство . Нормы:

Пусть , – операторы "сужения", действующие согласно равенствам:

где ;

Пусть далее , – проекторы. Зададим приближенную схему уравнения (1), полагая на -ом шаге

(4)

(5)

Будем говорить, что приближенная схема (4), (5) аппроксимирует уравнение (1) на решении , если:

Теорема 1. Пусть удовлетворяет условию (). Тогда: a) Уравнение (1) имеет решение , если только . b) Если , то приближенная схема (4)-(5) аппроксимирует уравнение (1) на .

Пусть – последовательность решений уравнения

Будем говорить, что приближенная схема (4)-(5) сходится на , если

Теорема 2. Пусть удовлетворяет условию () и пусть решение уравнения (1) . Тогда приближенная схема (4)-(5) сходится на .

Литература:

1. Наймарк М.А. Линейные дифференциальные операторы. – 2-е изд. – М.: Наука, 1969. – 528 с.

2. Треногин В.А. Функциональный анализ. – 3-е изд. – М.: ФИЗМАТЛИТ, 2002. – 488 с.

3. Отелбаев М., Кусаинова Л. К. Оценки спектра одного класса дифференциальных операторов // Збірник праць Інституту математики НАН України Теорія операторів, диференціальні рівняння і теорія функцій. – Київ, 2009. – Т. 6. – № 1. – С. 165-190.