Математика/3. Теория вероятностей и
математическая статистика
Бураковский В.В.
Гомельский государственный университет
им. Ф. Скорины, Беларусь
ИССЛЕДОВАНИЕ
СТАЦИОНАРНОГО РЕЖИМА В СМО
С НЕСКОЛЬКИМИ
ПРИБОРАМИ И РАЗНОТИПНЫМИ
ТРЕБОВАНИЯМИ
Рассмотрим СМО с ![]() приборами, в которую поступают заявки
приборами, в которую поступают заявки ![]() типов. Входящий поток
является простейшим с интенсивностью
типов. Входящий поток
является простейшим с интенсивностью ![]() , но таким, что с вероятностью
, но таким, что с вероятностью
![]() , каждая заявка независимо от предыдущих оказывается
, каждая заявка независимо от предыдущих оказывается ![]() -го типа.
-го типа.
Если поступающая в СМО заявка застает приборы
занятыми, то она становится в очередь, которая может быть неограниченной.
Обслуживание производится в порядке поступления. Заявки разных типов отличаются
тем, что требуют различного обслуживания. Время обслуживания в СМО распределено
по показательному закону с интенсивностью ![]() , где
, где ![]() – тип заявки. Для
определенности будем предполагать, что
– тип заявки. Для
определенности будем предполагать, что ![]()
Состоянием СМО будем называть вектор, состоящий из ![]() числа
числа ![]() , где
, где ![]() – количество заявок,
находящихся в СМО,
– количество заявок,
находящихся в СМО, ![]() – номер типа заявки,
обслуживаемой на первом приборе;
– номер типа заявки,
обслуживаемой на первом приборе; ![]() – номер типа заявки,
обслуживаемой на
– номер типа заявки,
обслуживаемой на ![]() -м приборе;
-м приборе; ![]() – номер типа заявки,
обслуживаемой на
– номер типа заявки,
обслуживаемой на ![]() -м приборе. Если в СМО
заявок нет, то для унификации обозначений будем говорить, что она находится в
состоянии
-м приборе. Если в СМО
заявок нет, то для унификации обозначений будем говорить, что она находится в
состоянии ![]() .
.
Предположим, что в СМО существует стационарный режим.
Через ![]() обозначим
стационарную вероятность того, что СМО находится в состоянии
обозначим
стационарную вероятность того, что СМО находится в состоянии ![]() . Процесс изменения состояний в СМО будет марковским.
Суммируя уравнения равновесия, получим следующее уравнение:
. Процесс изменения состояний в СМО будет марковским.
Суммируя уравнения равновесия, получим следующее уравнение:
![]() . (1)
. (1)
Данное соотношение получается при рассмотрении такого
сечения в графе изучаемой СМО, которое отделяет состояние ![]() от состояний
от состояний ![]() .
.
Состояние СМО, вообще говоря, задается вектором,
состоящим из ![]() числа
числа ![]() . Однако, если перенумеровать упорядоченные наборы
. Однако, если перенумеровать упорядоченные наборы ![]() через
через ![]() , то состояние СМО может задавать парой чисел
, то состояние СМО может задавать парой чисел ![]() . Если
. Если ![]() , то пара
, то пара ![]() соответствует состоянию
соответствует состоянию
![]() , при
, при ![]() пар вида
пар вида ![]() всего
всего ![]() , а в случае
, а в случае![]() таких состояний
таких состояний ![]() .
.
Будем называть множество ![]()
![]() -ым уровнем. Обозначим через
-ым уровнем. Обозначим через ![]() вектор стационарных
вероятностей
вектор стационарных
вероятностей ![]() -го уровня. Очевидно, что с каждого уровня можно перейти на
соседний, а при
-го уровня. Очевидно, что с каждого уровня можно перейти на
соседний, а при ![]()
![]() , при
, при ![]()
![]() , при
, при ![]() имеем
имеем ![]() .
.
Для стационарных вероятностей состояний выполняются
следующие соотношения6
p![]() = 0, pfl = 1,
(2)
= 0, pfl = 1,
(2)
где
![]() , fl – единичный вектор-столбец,
, fl – единичный вектор-столбец, ![]() – инфинитезимальная матрица, имеющая следующий блочный вид
– инфинитезимальная матрица, имеющая следующий блочный вид
![]() .
.
Для ![]() введем следующие
обозначения:
введем следующие
обозначения: ![]() при
при ![]()
![]() ,
, ![]() , при
, при ![]() .
.
Из соотношения p![]() = 0 имеем с учетом обозначений
= 0 имеем с учетом обозначений
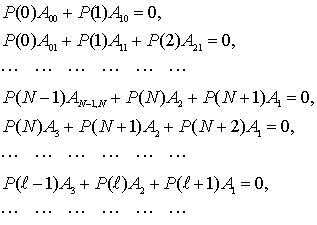 (3)
(3)
Для
построения блоков ![]() введем следующие обозначения:
введем следующие обозначения:
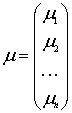 – вектор-столбец
интенсивностей обслуживания заявок различных типов, через
– вектор-столбец
интенсивностей обслуживания заявок различных типов, через 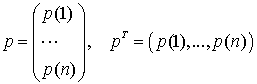 ,
, ![]() – единичная
– единичная ![]() матрица.
матрица.
С учетом этих обозначений получаем, что блоки ![]() имеют вид
имеют вид
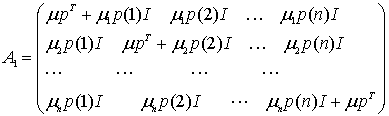 .
.
Таким
образом, ![]() имеют размерность
имеют размерность ![]() и состоят из блоков
и состоят из блоков ![]() , которые можно записать в виде:
, которые можно записать в виде: ![]() , где
, где ![]()
Блоки ![]() также имеют
размерность
также имеют
размерность ![]() и диагональный вид
и диагональный вид
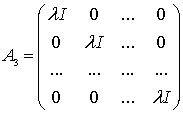 .
.
Блоки ![]() диагонального вида
диагонального вида
![]() размерности
размерности ![]() .
.
Для стационарных вероятностей можно записать
![]() (4)
(4)
Таким
образом, последнее соотношение из (3) будет иметь вид:
![]() (5)
(5)
Введем следующие обозначения: 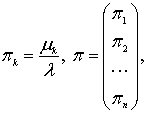
![]()
Учитывая
вид блоков ![]() , получим:
, получим: ![]()
![]() (6)
(6)
где
![]() – символ
кронекеровского произведения.
– символ
кронекеровского произведения.
Последнее соотношение из (3) примет
вид:
![]() (7)
(7)
или
с учетом (4)
![]() (8)
(8)
Таким образом, учитывая (4), имеем
![]() (9)
(9)
Полагая
![]() ,
,
![]() (10)
(10)
получим,
что ![]() при
при ![]() по методу Ньютса [1].
по методу Ньютса [1].
Литература
1. Neuts,
M.F. Matrix-geometric solutions in stochastic models : An algorithmic approach.
– The John Hopkins University Press. – Baltimore, MD. –1981. – 332 p.