Математика / 5. Математичне моделювання

Нестеренко О.Є, магістрант

Бердянський державний педагогічний університет

Математичні моделі розрахунку розміщення туристів з використанням теорії масового обслуговування

Мінімізація часу знаходження в черзі одне з основних питань, яким займається теорія масового обслуговування. Ця теорія застосовується для ощадливого проектування систем, призначених для задоволення масового потоку заявок випадкового характеру. Випадковими можуть бути як моменти появи вимог, так і витрати часу на їхнє обслуговування. Простим прикладом об’єктів теорії масового обслуговування можуть бути автоматичні телефонні станції, виїзди медичних машин швидкої допомоги, різні пристрої для збору й обробки інформації й тощо. У той же час проблеми, що вимагають застосування тих же математичних методів, виникають при автоматизації виробництва, організації транспорту, зв’язку й постачання.

Становленню теорії масового обслуговування ми зобов’язані датському інженеру А. Ерлангу, який займався розв’язком задач, що виникають в організації телефонних мереж. Далі в роботах К. Пальма, Ф. Поллачека,
А.Я. Хінчіна [3], Б.В. Гнеденко [1] дослідження в даному напрямку були плідно продовжені. Будучи частиною теорії випадкових процесів, теорія масового обслуговування виділилася в самостійну область досліджень зі своїм колом задач і методами їхнього розв’язку й у свою чергу стимулює розвиток теорії випадкових процесів. Розвиток теорії значною мірою стимулюється розширенням кола її застосувань.

Метою доповіді є дослідження моделі теоретичні основи розрахунку паралельних місць для туристичного комплексу та розрахунку необхідної кількість номерів для прийняття заявок.

Щодня в житті й діяльності людей створюються ситуації, коли виникає масовий попит на яке-небудь спеціальне обслуговування, причому обслуговуюча організація не завжди здатна задовольняти всі заявки, що поступають, оскільки має у своєму розпорядженні лише обмежену кількість обслуговуючого персоналу.

Головною задачею теорії масового обслуговування є встановлення взаємозалежності між числом обслуговуючих одиниць і якістю обслуговування. При цьому якість обслуговування в різних випадках вимірюється різними показниками. У більшості випадків таким показником слугує або відсоток заявок, що одержують відмову, або середній час очікування початку обслуговування. Зрозуміло, що якість обслуговування при цьому тим вище, чим більше число обслуговуючих одиниць. Однак надмірний ріст цього числа пов'язаний із зайвою витратою сил і матеріальних засобів. Тому спочатку встановлюється необхідний рівень якості обслуговування, а потім – мінімальне число обслуговуючих одиниць, при якому цей рівень може бути досягнутий. [2, c.68]

При розв’язувані задач майже завжди необхідно враховувати вплив випадкового елемента на потік досліджуваного явища. Кількість заявок, що поступає не є постійною, а випадково коливається. Час обслуговування заявок також не є стандартним, а випадково коливається від однієї заявки до іншої. Всі ці елементи випадковості не мають характеру невеликих «збурювань», що порушують собою плавний і закономірний хід явища; навпаки, вони становлять собою основну рису в картині досліджуваних процесів. [4, c.96]

У теорії масового обслуговування потік вимог описується за допомогою пуассонівського процесу, що описує моменти настання яких-небудь випадкових подій. У пуассонівському процесі число подій, що відбуваються протягом будь-якого фіксованого інтервалу часу, має розподіл Пуассона й незалежні числа подій, що відбуваються в непересічні проміжки часу. Потік подій, що має властивості стаціонарності, ординарності й відсутністю наслідку, визначається як найпростіший або пуассонівський потік.

Припустимо – число подій, моменти, настання яких задовольняють нерівностям , і нехай – математичне сподівання . У цьому випадку пуассонівський процес при будь-яких випадкові величини , , …, незалежні й імовірність того, що , дорівнює .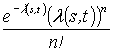

В однорідному пуассонівському процесі де - середнє число подій в одиницю часу, відстані між сусідніми моментами незалежні й мають показовий розподіл із щільністю .

Розподіл Пуассона досить розповсюджений і важливий розподіл, що застосовується як у теорії ймовірностей, так і в математичній статистиці. Багато практичних задач зводяться, в остаточному підсумку, саме до розподілу Пуассона. Він використовується у тому випадку, коли число незалежних випробувань велике, а ймовірність появи події в кожному окремому взятому випробуванні досить мала. [3, c.158]

Випадкова величина має розподіл Пуассона, якщо її можливі значення 0, 1, 2, …, (нескінчена, але зчисленна множина значень), а їх відповідна ймовірність появи події раз у випробуваннях, виражаються формулою:

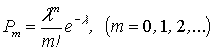
де – математичне сподівання, або середнє число появ події у випробуваннях.

Зміст параметра полягає в рівності одночасно й математичному сподіванню й дисперсії випадкової величини, розподіленої за законом Пуассона, тобто .

Актуальним є застосування всіх можливостей сучасного системного моделювання й математичних методів для вибору стратегії розвитку туристичного бізнесу при розв’язуванні практичних задач модернізації туризму в Україні.

Наявність засобів розміщення й кількість місць у них є важливим показником туристського потенціалу курортних зон. Оскільки в нашому регіоні спостерігається диференціація засобів розміщення за рівнем комфортності, кількість місць у готелях з більше кращими умовами може виявитися обмеженою. Обмеження місць розміщення в готелі приводить до втрати певного числа клієнтів. Особливо яскраво цей момент проявляється в період курортного сезону.

Проаналізувавши теоретичні аспекти необхідності застосування теорії масового обслуговування в туризмі за допомогою математичного моделювання загального числа заявок від туристів у туристичний комплекс автором розроблена модель визначення кількості номерів з обліком ризикованих інвестиційних вкладень.

Для розробки моделі необхідно досліджувати функцію розподілу випадкової величини: числа заявок, що поступають за час t.

Для цього потрібно проаналізувати статистичні дані за кількістю місць в одному з туристичних комплексів . Виявилося, що випадкова величина X числа заявок за час t, що надходять для оформлення розподілена за законом Пуассона, тобто ймовірність того, що X прийме певне значення т, виражається формулою:

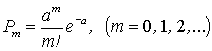(1)

де – деяка додатна – величина, яка називається параметром закону Пуассона. Відомо, що в розподілі Пуассона параметр дорівнює математичному сподіванню випадкової величини, а дисперсія випадкової величини, розподіленої за законом Пуассона, дорівнює її математичному сподіванню, тобто .

Ця властивість часто застосовують на практиці для рішення питання правдоподібності гіпотеза про те, що випадкова величина розподілена за законом Пуассона.

Потік заявок, як установлено, є випадковим пуассонівським процесом

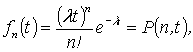(2)

де – ймовірність того, що за час надійде в туристичний комплекс рівно n заявок; – середнє число заявок в одиницю часу. Формулу (2) можна інтерпретувати в такий спосіб. Фіксуємо час на рівні заданого нормативу часу прийняття заявки в даному туристичному комплексі. Фіксуємо також на рівні вільних номерів для недопущення нагромадження заявок у черзі. У цьому випадку з рівняння

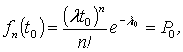(3)

можемо одержати невідому величину n, що позначає, яку кількість заявок необхідно прийняти туристичному комплексу за час , щоб гарантувати заселення для всіх заявок з імовірністю . Знайшовши з рівняння (3) величину , обчислимо необхідне число номерів, щоб виконати нормативи часу й гарантії . Для цього досить знати середнє число заявок , що може виконати один туристичний комплекс в одиницю часу. Тоді число паралельних каналів оформлення й контролю вантажів N визначається за формулою:

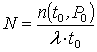(4)

Розв’язок рівняння (3) можна одержати, застосувавши наступний метод. Перепишемо (3) у вигляді: .

Прологарифмувавши праву й ліву частини цього рівняння, одержимо:

. Звідси маємо:

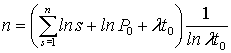(5)

З огляду на, що за змістом n ціла величина, як правило, невелика, розв’язок рівняння (5) можна одержати методом простого перебору n або методом дихотомій при , де - деяке ціле число.

Отже, досліджена модель може бути використана в туристичному комплексу для обчислення необхідного числа номерів для прийняття заявок від туристів. При цьому враховувався заданий рівень необхідного заселення й недопущення нагромадження заявок у черзі.

ЛІТЕРАТУРА

1. Гнеденко Б.В. Введение в теорию массового обслуживания / Б.В. Гнеденко, И.Н. Коваленко. – М. : Наука, 1966. – 432 с.

2. Теорія і методи соціальної роботи: навч. посіб./ М.П. Лукашевич,
І.І. Мигович. – 2-ге вид., доп. і випр. – К. : МАУП, 2003. – 168 с.

3. Управління сучасним готельним комплексом: навч. посіб. / За редакцією члена-кор. НАН України, д.е.н., професора С.І. Дорогунцова– К. : Ліра-К, 2005. – 520 с.

4. Хинчин А.Я. Работы по математической теории массового обслуживания / Под редакцией Б. В. Гнеденко. – М. : Физматгиз, 1963. – 236 с.