Ж.Б. БАКИРОВ, М.Ж. БАКИРОВ

Карагандинский государственный технический университет

Стационарные случайные колебания подвески автомобиля

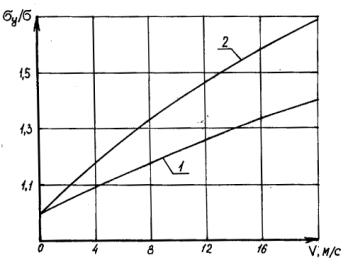
Простейшую динамическую модель ходовой части автомобиля можно представить в виде, показанном на рисунке 1. Здесь m – подрессоренная масса, приходящаяся на одну подвеску; С, α – коэффициент жесткости и диссипативных сил сопротивления; у₀ – кинематическое воздействие, зависящее от высоты микропрофиля дороги h(x).

Уравнение движения модели имеет вид

,

где у₀=у₀(t) – является функцией времени. Это уравнение можно переписать так:

, (1)

где ; .

Функцию у₀ (t) можно найти делением высоты микропрофиля дороги на скорость движения V. Если V = 1 м/с, то функция и у₀ совпадут.

Микропрофиль дороги является случайной функцией от протяженности пути. Условно дороги разбивают на ряд типов в зависимости от среднеквадратичной высоты неровностей. Статистическая обработка результатов замера микропрофилей данного класса дорог позволяет получить их вероятностные характеристики. Подробные сведения об этих характеристиках можно найти в специальной литературе [1].

При прочих равных условиях величины и чередования импульсов сил, действующих на машину при движении по определенному участку дороги с постоянной скоростью , не зависят от того , когда машина проезжает данный участок . Следовательно , воздействие дороги на машину будет стационарным случайным процессом. Корреляционные функции этих воздействий могут быть описаны функциями [1].

, , (2)

где - стандарт высоты неровностей; α – коэффициент широкополостности процесса; β – несущая частота.

Параметры этих функций зависят от типа дороги и скорости движения. Их можно представить в виде явной зависимости от скорости

; ,

где - значения параметров при единичной скорости движения, зависящие только от типа дороги.

Рассмотрим стационарные колебания при стационарном кинематическом возбуждении. В этом случае целесообразно применить спектральный метод. Переходная функция, имеющая смысл динамической податливости, для уравнения (1) имеет вид

, (3)

а спектральная плотность решения определяется по формуле.

, (4)

где L- оператор, имеющий смысл динамической жесткости; - спектральная плотность воздействия дороги на автомобиль.

Корреляционная функция решения при необходимости находится преобразованием Фурье

. (5)

Этот интеграл обычно вычисляется по теореме вычетов.

Часто для расчета подвески достаточно знать дисперсию колебаний:

. (6)

Вычисление этого интеграла сводится к вычислению стандартного интеграла вида:

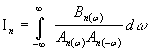, (7)

где и - полиномы с комплексными коэффициентами:

;

.

Все корни должны лежать в верхней полуплоскости. Формулы для интегралов (6) при различных n приведены в работе [2].

Пусть внешнее воздействие имеет корреляционную функцию в виде первого выражения (2). Тогда спектральная плотность

. (8)

Спектральную плотность выходного процесса определяем по формуле (4)

,

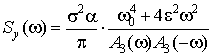где .

Определим корреляционную функцию, интегрируя (5) по теореме вычетов

,

где - корни полинома , лежащие в верхней полуплоскости:

, , ; .

С учетом этих соотношений запишем

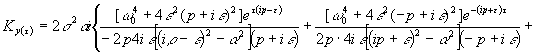
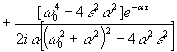
После несложных математических преобразований и распространения результатов на всю ось τ получим

+.

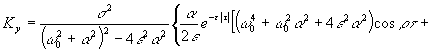
При t =0 отсюда находим дисперсию

(9)

Явную зависимость дисперсии от скорости движения в безразмерном виде можно записать так

,

где , .

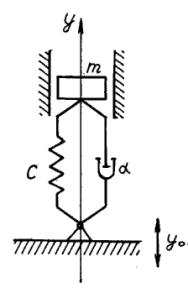
На рисунке 2 показаны графики изменения дисперсии колебаний от скорости движения машины при n=0,05 и различных m.

Рисунок 1	Рисунок 2
Динамическая модель подвески	График изменения дисперсии перемещения 1.- m=0,005; 2.- m =0,01.

Рассмотрим теперь корреляционную функцию, определяемую вторым выражением соотношений (2). Спектральная плотность воздействия в этом случае имеет вид

. (10)

Определим дисперсию колебаний подвески по формуле (6)

,

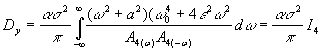где ; .

Здесь интеграл вида (7), а коэффициенты полиномов будут равны:

,

.

Интеграл определяется через коэффициенты полиномов следующим образом [2]

.

Подставляя сюда коэффициенты, находим

. (11)

При β=0 совпадают корреляционные функции (2); в этом случае (а²=α²) совпадают и дисперсии (9) и (11).

Во многих прикладных задачах возникает необходимость определения вероятности того, что вертикальное смещение массы не превысит заданного уровня ( не произойдет «пробой» подвески ). Считая, что для перемещения имеет место нормальное распределение с параметрами и , искомую вероятность можно определить по формуле

.

Для расчета подвески на прочность и долговечность необходимо знать вероятностные характеристики динамической составляющей нагрузки, которая является случайной функцией. Для рассматриваемой модели в виду малости коэффициента сил сопротивления можно записать

,

где С – жесткость подвески.

Корреляционная функция случайной силы равна

.

Применяя преобразование Фурье, получаем связь между спектрами

.

Так как спектры входного и выходного процесса связаны соотношением

,

то умножая обе части этого равенства на спектр и осредняя с учетом ортогональности спектра , получаем

.

С учетом этого соотношения и формулы (4) ,находим

.

После подстановки выражения (3) , получаем

.

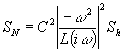Корреляционная функция силы находится по формуле типа (5). Для спектральной плотности (8) имеем

.

Интегрируя это выражение по теореме вычетов, получаем

.

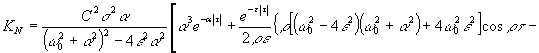
Тогда дисперсия силы равна

.

Литература:

1. Яценко Н.Н. Колебания, прочность и форсированные испытания грузовых автомобилей. -М.: Машиностроение, 1972. 372 с.

2. Болотин В.В. Методы теории вероятностей и теории надежности в расчетах сооружений. –М.: Стройиздат, 1981. 351 с.