Екологія / 6. Екологічний моніторинг

К.т.н. Холковський Ю. Р., к.х.н. Кофанова О. В., студ. Березівський М. Ю.

Національний авіаційний університет України, Національний технічний університет України "КПІ", Державний заклад "Київський коледж зв’язку"

МОНІТОРИНГ ЕКОЛОГІЧНИХ ПРОЦЕСІВ І СИСТЕМ
ІЗ ЗАСТОСУВАННЯМ дискретно-інтерполяційнОГО підхОДУ

Екологічний моніторинг − інформаційна система спостережень, оцінювання й прогнозування змін у стані компнентів довкілля, призначена для виокремлення антропогенної складової на фоні природних біосферних процесів. В умовах сучасної глобальної екологічної кризи, неконтрольованого впливу людини на навколишнє середовище робота з організації екологічного моніторингу набуває особливої значущості.

Природні екосистеми тісно взаєпов’язані одна з одною, тому моделювання, прогнозування й контроль стану компонентів довкілля є складним, багатопараметровим і стохастичним процесом. Запропонована авторами технологія полягає у виборі оптимальних методів моделювання складних багатопараметрових екологічних процесів і систем, прогнозування екологічної безпеки певної території та процесів, що відбуваються на ній. При моделюванні екосистем, що не піддаються аналітичному опису, доцільно, на наш погляд, використовувати геометричні моделі (точкові або лінійні) у вигляді дискретних чисельних масивів.

У багатьох задачах геометричного моделювання виникає необхідність побудови однопараметрової множини різних математичних об’єктів і процесів. Таким об’єктом може бути деяка поверхня або гіперповерхня, як модель певного середовища, що задана аналітично, а частіше дискретно. Вибір інтерполяційних поліномів Лагранжа серед певної кількості різноманітних інтерполяційних поліномів вважається нам оптимальним. Це зумовлено не обов’язково рівномірним розташуванням вузлів інтерполяції, а також можливістю представлення по кожній змінній різної кількості вузлів інтерполяції.

Під терміном "вузли інтерполяції" надалі розуміємо не точки, а складніші об’єкти − лінії та поверхні або навіть певні процеси, що представлені у вигляді деяких функціоналів як сукупності їх властивостей і параметрів. Схема розташування вузлів інтерполяції розуміється як схема інтерполяції.

Одержані таким чином однопараметрові множини є дискретними математичними моделями певних процесів і систем, у тому числі й екологічних. Елементом таких множин є деяка дискретна функція, що у загальному випадку може бути представлена як дискретний чисельний масив, розмірність якого може варіюватись у певних межах. Інтерполювання функцій, які можуть бути задані неявно або параметрично, зводиться до розміщення у вузлах інтерполяції рівнянь або дискретних масивів і отримання деякого функціонала з вектором параметрів, що включає в себе інтерполяційний параметр, координатні змінні, параметри, що характеризують форму й положення об’єктів, параметричні характеристики процесів тощо.

Такий підхід надає змогу включати в однопараметрову множину системи та процеси, що мають різну структуру і навіть різні властивості. Тому перспективним є застосування такого підходу до моделювання складних екологічних систем, а також середовищ, що характеризуються великою кількістю різноякісних параметрів.

Дискретний підхід можна вважати більш загальним, оскільки від неперервно-аналітичної моделі практично завжди можна перейти до дискретної, а в нашому випадку − до дискретно-інтерполяційної. Отже, за нашого підходу поліном Лагранжа набуває вигляду:

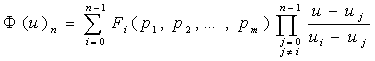(1)

де u – параметр інтерполяції, F(p₁, p₂, …p_k) − вузлова функція, p₁, p₂, … p_k – параметри вузлової функції, n – кількість вузлів інтерполяції.

У випадку двовимірної інтерполяції можна знайти вид степеневого многочлена Ф_m,n(u,v) степеня m по u та n по v та визначити значення функціонала F у довільній точці з параметрами (u,v). Геометрично це означає, що при двовимірній інтерполяції через вузлові точки проходить певна поверхня z = Ф_m,n(u,v).

Якщо побудувати регулярну сітку та задати у вузлах сітки значення функції z, то вся площадка розпадається на mn прямокутників, в один з яких і потрапить точка (u,v). Відбувається інтерполяція при різних u_i, но фіксованих v_j, після чого необхідно перейти до v_j+1 і повторити знову всю процедуру.
У такому випадку отримуємо двовимірну інтерполяцію P_m,n(x,y) степеня m по x і степеня n по y z(x,y) у довільній точці T(x,y). При цьому через вузлові точки проходить поверхня z = P_m,n(x,y). Отже, отримуємо формулу для двовимірної інтерполяції за Лагранжем:

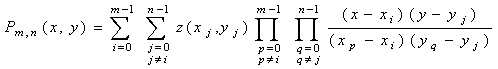(2)

У випадку n-мірної інтерполяції через вузлові точки проходить певна гіперповерхня, що є многочленом n змінних, а формула матиме аналогічний вигляд.

Важливим фактором є введення певного критерію інтерполяції. Це пов’язано з тим, що, інтерполяційний поліном фактично є зрізаним рядом (аналогом ряду Тейлора) внаслідок того, що він обмежений степенем n. Тому для збіжності відповідного аналога ряду Тейлора необхідно спадання абсолютної величини коефіцієнта при u з ростом степеня u. Тому критерієм гарної апроксимації у випадку багатовимірної інтерполяції є спадання абсолютних величин похідних по всіх змінних із зростанням їх порядку.

Таким чином, запропонований нами підхід дає змогу не тільки моделювати складні екологічні системи, процеси і середовища, що характеризуються великою кількістю різноманітних параметрів і властивостей, але й прогнозувати поведінку екосистем, розвиток певних процесів тощо.