Economic sciences/ 8.Mathematical methods in economics
Kostikina D., Kilincel T.
Saint-Petersburg State University, Russia
The application of the theory of cooperation
games in research of Russian-Turkish processes of economic collaboration.
Investigation of the
processes and principles of cooperation is interesting, relevant and important
direction, which is caused by a number of reasons: in the current economic and
geopolitical situation the trend of mutual approach between Russia and Turkey
is growing. On the one hand it is due to crisis in the economy of Western
Europe so Europe has to solve its own problems. The crisis on Cyprus is a
striking example of attempts to tackle European economic problem at the expense
of Russian business. On the other hand China as a principal partner of Russian
Federation on the East cannot exhaust (satisfy) completely the interests of
Russia in spite of its size. Successful promotion of the fundamental interests
of Russia in the South European and the Middle East sector is impossible
without consistency of acts with Turkey. Of course, Turkey cannot be considered
as a simple and hassle-free partner, the presence of common interests does not
mean the absence of conflicts and problems on both sides. From the above it
should first be concluded that these problems and contradictions should not be
left in the dark, they should be studied, including the use of
economic-mathematical methods. In our opinion an adequate instrument of
modeling process unfolding in the sphere of Russian-Turkish cooperation is the
methodology of game theory as in the center of these problems is the issue of
cooperative interaction.
The history of
Russian-Turkish relations has more than 5 centuries, but most of this time
between two countries were countless wars. Economic and investment cooperation
between Russia and Turkey began in the 30s of the 20th century, but
with the beginning of the Second World War it was interrupted and resumed in
the 60s.
Among the most famous
examples of cooperation between Russia and Turkey may be mentioned: the
construction of APS “Akkuyu” in the province of Mersin (20 billion dollars),
the construction of “Technostroyexport” in the consortium of the dam and
hydroelectric power station “Deriner” (100 billion dollars), the construction
of the gas pipeline “South Stream” in the Black Sea, which will connect Russia
with the countries of Southern Europe, the construction of a car factory GAZ in
the Turkish province of Sakarya with the participation of the Russian side in
the face of “GAZ Group” company and the Turkish side in the face of “Mersa
Otomotiv”.
Of course, these
examples are characterized by complexity and versatility. Their appropriate
study involves the use of quite a diverse and dissimilar economic models. In
this case we will focus attention exactly on the cooperative effects inherent
these models.
Lately, Russia and
Turkey actively cooperate in the automotive industry. According to newspaper
reports Russian automotive group "GAS" and the Turkish distributor
"Merce Automotive" recently opened a car factory of GAZ commercial
vehicles in the Turkish province of Sakarya, also Russian and Turkish partners
will open a dealership and service network. GAZ cars will be sold not only at
the Turkish market but also in Europe, North Africa and the Middle East.
Existing difficulties
on political issue will not influence on the obvious successes of the economic
cooperation between two countries, in spite of deep differences over the Syrian
issue the cooperation between two countries continues to strengthen. Maybe this
project will be the basis for long-term cooperation in the automobile industry
between Russia and Turkey.
According to
provisional data by the end of 2012 the company plans to produce 300 GAZ
minibuses model "gazelle-business", and in 2013 production will
increas to 2,500 cars with the prospect of increasing to 3700. There is an
unoccupied niche of light commercial vehicles in Turkey and"GAZ
Group" together with the Turkish company "Merce Automotive",
which invested in the project 15 million euros, claim to it. The partners'
plans are to win 7-10 percent of the local car market. Assembled in Turkey GAZ
automobiles will be cheaper than the products of the competitors for 15-20%.
The price will work out at 38,400 liras (about 21,300 U.S. dollars).
Until recently only 3
companies mostly produced vans in Turkey: Ford Otosan, which produces on average
19,371 cars per year, Karsan (2936) and Otokar (168). Since 2013 GAZ company
has begun to produce in Turkey, which is also planning to produce vans
initially in the amount of 2500. Given the fact that in 2012 it turned out that
Ford had 86% of the whole minibus
market share in Turkey, for two other companies (Karsan and Otokar) would be
profitable to unit with the new company GAZ if their total winnings for each
company will be more than if the company had not entered into a coalition. At
the simplest level for the situation of the cooperation of both sides in the
project, which unites three participants, may be suggested the next
game-theoretical cooperative model.
Part of the game
theory, where players can form a coalition called the theory of cooperative
(coalitional) games. We assume that this game is a game with transferable
utility. Our cooperative game we denote by a pair (I, v), where the I-set of
players, and v - the characteristic function, and any subset S of the set I are
called coalitions of players. The characteristic function of a cooperative game
is a function that each possible coalition S assigns to the utility (win) which
the coalition can get.
In out case we get:
– that means that the Otokar company produce
by itself 168 cars per year and occupies 1% of the market.
– characteristic function of a player Karsan.
– characteristic function of a player GAZ.
If the
first and the second player join up their characteristic function is: 
The same
for other integrations: 
; 
The characteristic
function for 3 players:
Thus, it
appears that due to combining all three players can get 33% of the market.
Allocating a prize,
which will be estimated at the number of vehicles manufactured by each company,
the capacity constraints of the plants must be taken into account: Otokar no
more than 1500, Karsan no more than 16 300, GAZ no more 3700.
The game is superadditive: 
And convex: 
The
basic concept for the game theory is the concept of imputation. In cooperative
game (I, v) imputation is a vector x = (x1, ..., xi, ...,
xn) (n = | I |-the number of players), which satisfies the
conditions:
·
- the condition of
group rationality, i.e. imputation must completely distribute utility receives
by combining all the players in the coalition.
·
- the condition of individual rationality,
i.e. imputation should give the player as much as he can get, without entering
into any of the coalitions, where 
is the utility that must be given to player
i.
- the utility, that coalition S should
receive: 
If the vector x
satisfies only the conditions of group rationality, it is called a
pre-imputation or distribution.
The solution of a
cooperative game should give us the answer to the question: what shares can the
players count on in the win of the grand coalition v(I)? Reasonable solution to
the cooperative game is to find the Shapley value. According to the Shapley
value the share of the player i in the imputation is:
where s=|S| - the number of players in
coalition.
Imputation x
dominates imputation y of the coalition S, if:
The first condition
means that the imputation x is more profitable than the imputation y for all
members of the coalition S, and the second condition means that the coalition S
can actually provide it due to its win v(S).
Imputation x
dominates y if there is an imputation of at least one coalition on which it
occurs.
Core - is the set of
undominated imputations in the game (I, v), it is denoted C(v).
It’s simple to show, that: 
Core is
a set of imputations that cannot be objectively challenged by any of the
coalitions. This solution is associated with two fundamental problems:
1. In certain
situations, core can be very large, what makes the choice of preferred
imputation of it ambiguous.
2. In some cases,
core may be empty.
If the game is
convex, the Shapley value always belongs to core, but if the game is
superadditive and is not convex, the Shapley value cannot belong to core even
if it is not empty.
Now we will show a
geometric interpretation for the core in the considered game. It is possible
because the game gets three players, and therefore imputations and
pre-imputations are vectors in three-dimensional space. Then the condition of
group rationality takes the form:
For this condition
there is a plane in three-dimensional space, which intersects the axes at the
points: (0,33;0;0), (0;0,33;0), (0;0;0,33).
Conditions of
individual rationality of players: 
These inequalities "cut" from
the plane the triangle, i.e. set of imputations in the game is a 3-simplex with
vertices (0.33, 0, 0), (0, 0.33, 0), (0, 0, 0.33). Set of points on the plane
are the pre-imputations in this game.
Also the constraints
on the coalitions must be considered:
(1)
This means that the imputation belonging to core
should not give in the coalition of the first and second players less than
0.15, or they had better not join up into the coalition of three players. For
similar reasons:
(2)
(3)
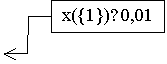
000
(0;0;0,33) (0;0,33;0) (0,33;0;0)
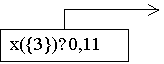
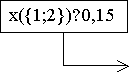000
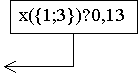000
000
00
0
0
0
0251689984
D
00
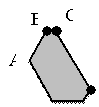
Picture 1. Geometric
characterization of the core.
The set of imputations satisfying (1), is
"above" the plane 
, and the set of imputations that
satisfy the condition (2) is above the plane 
, for condition (3) - above the
plane 
. The result of their intersection
with the plane gives a figure marked by grey color. This figure is the locus of
points that belong to the core of the game. This game model is one of those
situations where the core is large enough. Thus, in this situation, to find a
reasonable solution that satisfies all the constraints, it is sufficient to
calculate the Shapley value: 
; 
;
Thus it turns out that when the first player
joins to the grand coalition he gets 3% of the market, the second - 16%, and
the third - 14%, and together they will take 33% of the market, therefore, the
market share for Ford reduces and becomes 67% against 86%.
Also we can count the values in the points of
extremum:
A=(0,05;0,13;0,15),
B=(0,02;0,13;0,18), C=(0,01;0,14;0,18), D=(0,01;0,2;0,12), E=(0,02;0,2;0,11),
F=(0,05;0,17;0,11)
It should be noted that this model uses a relative income of firms, i.e. we assume that the income linearly proportional to the market share and is assumed to be some constant: const • α, where α - market share. Therefore, in the calculation examples we directly the value of the market share.
Among the present-day
works in which the problems of application of methods of game theory to solve
the problems of economic collaboration are considered may be mentioned:
·
Konyukhovskiy
P., “The application of stochastic cooperative games in studies of regularities
in the realization of large-scale investment projects”, 2012
·
Konyukhovskiy
P., Malova A., Kylynchel T., “Comparative analysis of mobile
telecoomunication sphere in Russian Federation and Turkish Republic using
differential equations”, 2012
·
Konyukhovskiy
P., Malova A.,”The application of methods of game theory in analysis of
relations of collaboration between economic subjects”, 2012
·
Konyukhovskiy
P., “The application of stochastic cooperative games to justify the investment
projects”, 2012
These models are
certainly quite abstract and simplistic, but they can increase the level of
confidence in the research of future evolution patterns of Russian-Turkish
economic relations.
1. Pecherskiy
S., Belyaeva A., “Game theory for economists”, 2001
2. Kannai Y.,
“The core and balancedness”, 1992
3. Shapley L.S.,
“On balanced sets and cores”, 1967
4.
Konyukhovskiy
P., “The application of stochastic cooperative games in studies of regularities
in the realization of large-scale investment projects”, 2012
5.
Konyukhovskiy
P., Malova A., Kylynchel T., “Comparative analysis of mobile
telecoomunication sphere in Russian Federation and Turkish Republic using
differential equations”, 2012
6.
Konyukhovskiy
P., Malova A.,”The application of methods of game theory in analysis of
relations of collaboration between economic subjects”, 2012
7. Konyukhovskiy P., “The application of stochastic
cooperative games to justify the investment projects”, 2012
8. The
publication of the Chamber of Commerce and Industry
9. The
internet-publication www.pandia.ru
10. The
internet-publication of the radio station “The voice of Russia” http://rus.ruvr.ru
11. Automotive
manufacturers association http://www.osd.org.tr