Економічні науки/ 8. Математичні методи в економіці

Скрильник І.І., Окань Р.М.

Полтавський національний технічний університет, Україна

Прогнозування чистого доходу агрофірми «Урожай» на основі адаптивної моделі Хольта-Вінстона

Оскільки основною задачею соціально-економічного дослідження є побудова прогнозних моделей, що найкращим чином описують динаміку розвитку, то для цього при прогнозуванні еволюційних процесів та економічних показників використовують адаптивні методи та моделі, що дозволяють у більшій мірі враховувати поточну інформацію та в меншій мірі – минулу. Однією з таких моделей є модель експоненціального згладжування Хольта-Вінстона з урахуванням тренду та сезонності. Переваги методу Хольта-Вінстона – це можливість будувати прогноз на довгостроковий період.

Постановка задачі. За заданими значеннями чистого доходу агрофірми «Урожай» (табл. 1) побудувати прогноз чистого доходу підприємства на 2012 р., використовуючи модель Хольта-Вінстона. Визначити точність моделі та підібрати оптимальні коефіцієнти згладжування. Зробити висновок про адекватність отриманої моделі.

Таблиця 1

Чистий доход підприємства за 2009 – початок 2012 рр.

Рік	Місяці	Доход, млн. грн.	Рік	Доход, млн. грн.	Рік	Доход, млн. грн.	Рік	Доход, млн. грн.
2009	1	3181	2010	7100	2011	8120	2012	14219
	2	3350		7250		8350		14350
	3	3570		7290		8710
	4	4100		7290		9100
	5	4500		7430		10050
	6	4900		7500		11200
	7	5100		7650		11950
	8	6000		7580		12300
	9	6300		7700		12850
	10	6450		7890		13150
	11	6650		7910		13560
	12	7075		7963		13860

Розв’язання задачі. Адаптивна модель прогнозу Хольта-Вінтерса – це 3-х параметрична модель, яка враховує: згладжений експоненціальний ряд; тренд; сезонність.

Експоненціально-згладжений ряд розраховуємо за формулою:

. (1)

Значення тренду визначаємо за формулою:

. (2)

Виконуємо оцінювання сезонності:

, (3)

де – поточне значення ряду (наприклад, об’єм доходу); – згладжена величина на поточний період; – згладжена величина за попередній період; – коефіцієнт сезонності для поточного періоду; – коефіцієнт сезонності за той же період у попередньому сезоні; – значення тренду на поточний період; – значення тренда за попередній період; – коефіцієнт згладження ряду; – коефіцієнт згладження тренду; – коефіцієнт згладження сезонності.

Коефіцієнти згладження задаються вручну і знаходиться у діапазоні .

Для першого періоду на початку даних експоненціально-згладжений ряд дорівнює першому значенню ряду .

Сезонність у першому та другому періоді дорівнює 1.

Значення тренду для першого періоду дорівнює 0 ().

Коефіцієнти сезонності для першого сезону (року) дорівнює 1.

У роботі побудовано прогноз на періодів 2012 р. за формулою:

, (4)

де – прогноз за методом Хольта-Вінтерса на періодів вперед; – експоненціально-згладжена величина за останній період; – порядковий номер періоду, на який робимо прогноз; – тренд за останній період; – коефіцієнт сезонності на цей же період в останньому сезоні.

Отримані дані представлено у таблиці 2.

Таблиця 2

Прогноз чистого доходу підприємства на 2012 р.

Рік	Періоди, p	Доход, млн. грн.
2012
	1	14429,77
	2	14469,13
	3	14752,13
	4	14889,00
	5	14822,66
	6	14778,70
	7	15117,08
	8	15277,69
	9	15305,00
	10	15228,05

У роботі виконано оцінку точності побудованої адаптивної моделі. Також розраховано похибку моделі та точність прогнозу, що становить 99,9%. Для підбору коефіцієнтів згладженого ряду, тренду та сезонності при яких прогноз буде максимально точним, був здійснений перебір усіх значень у діапазоні від 0 до 1 та знайдено таке поєднання, при якому точність прогнозу максимально наблизилася до 100%. Отримані наступні значення: .

У роботі виконано візуалізацію отриманих результатів: на одній діаграмі побудовано фактичний ряд чистого доходу, експоненціально згладжений ряд та ряд з моделлю прогнозу (рис. 2).

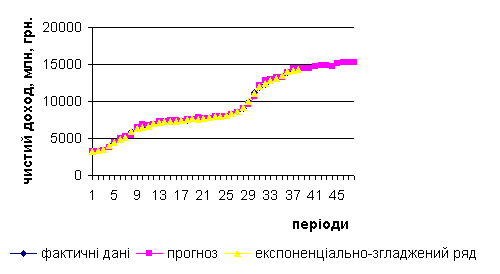
Рис. 2. Графік чистого доходу з прогнозом агрофірми «Урожай»

Встановлено адекватність моделі. Трендова модель вважається адекватною, якщо залишкові компоненти задовольняють таким вимогам: випадковість, що відповідає нормальному закону розподілу; рівність нулю математичного сподівання; незалежність значень (відсутність автокореляції). Було встановлено, що всі вимоги виконуються (табл. 3).

Таблиця 3

Виконання вимог до умов адекватності моделі

Умова випадковості залишків.	Метод піків, → 19>18.
Умова рівності математичного сподівання залишків 0.	tрозр. < tтабл., 0,376 < 2,026.
R/S-критерій, [3,47; 4,89].	4,37, 3,47<4,37<4<89.
Критерій Дарбіна-Уотсона, d1=1,41; d2=1,52.	; d=1,65; 1,52<1,65<2.

Прогнозна модель, побудована на основі методу Хольта-Вінстона є адекватною і її можна використати для визначення прогнозних значень чистого доходу підприємства на майбутні періоди.

Література:

1. Антохонова И.В. Методы прогнозирования социально-экономических процессов / И.В. Антохонова - Улан-Удэ: Изд-во ВСГТУ, 2004. - 212 с.

2. Лукашин Ю.П. Адаптивные методы краткосрочного прогнозирования временных рядов : учеб. пособие / Ю.П. Лукашин. – М. : Финансы и статистика, 2003. – 416 с.

3. Афанасьев В.Н. Анализ временных рядов и прогнозирование: Учебник. / В.Н. Афанасьев, М.М. Юзбашев. – М.: Финансы и статистика, 2001. – 200 с.
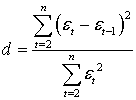