БИТЮКОВ Н.А.,
ФГУ «Сочинский национальный парк», г. Сочи, РФ
ИССЛЕДОВАНИЕ СКОРОСТНОГО КОЭФФИЦИЕНТА
В ФОРМУЛЕ ШЕ3И
ДЛЯ ОТКРЫТЫХ РУСЕЛ
Введение
Вопрос
об определении энергетических потерь в потоках жидкостей является одним из
важнейших в гидротехнике как с точки зрения теоретической, так и практической.
В практике гидротехнических расчетов открытых русел очень часто пользуются
формулой французского гидравлика Шези, предложенной им для равномерного
движения в руслах:
V = C∙
![]() , (1)
, (1)
где C= ![]() называют скоростным коэффициентом или
коэффициентом Шези.
называют скоростным коэффициентом или
коэффициентом Шези.
Как
величина коэффициента трения λ , так и величина коэффициента Шези,
характеризуют энергетические потери в движущихся жидкостях. До середины прошлого
века считали, что С (или λ ) должны быть постоянными
числами. Но практика опровергла это предположение и потребовала более глубокой
проработки вопроса.
Ввиду
сложности характера взаимодействия движущегося потока с вмещающим его в себя
руслом или другим водоводом гидравлические сопротивления большей частью
изучались с помощью экспериментов. Теоретические разработки в этой области
гидравлики сравнительно немногочисленны и в большинстве своем являются
слишком грубыми схемами тех процессов, которые происходят в потоках
жидкости. Сказанное относится в особенности к рекам в естественном состоянии.
В
настоящем исследовании сделан обзор методов и формул, применяющихся при
определении гидравлических сопротивлений в водотоках, и приведены некоторые
данные о коэффициентах сопротивления для нескольких горных рек Черноморского
побережья Кавказа.
1 Гидравлические сопротивления при ламинарном
и турбулентном режимах движения жидкости
Как
известно, движение жидкостей может быть различным в зависимости от условий, в
которых оно происходит, а именно: в ламинарном режиме и турбулентном. Оба эти
режима течения взаимосвязаны, могут переходить друг в друга, и являют собой
диалектический закон перехода количества в качество: наблюдающееся при малых
скоростях ламинарное движение с увеличением скорости течения сменяется турбулентным.
Закон изменения сопротивлений, а следовательно, и коэффициент С, связаны с родом движения.
При
ламинарном режиме движения гидродинамические сопротивления в потоке образуются
под действием сил внутреннего трения, или вязкости жидкости. Согласно закону
Ньютона о вязкости, внутри движущейся жидкости возникают касательные
напряжения, величина которых в каждой точке потока пропорциональна значению
пространственной производной скорости в этой точке:
![]() (2)
(2)
При
движении жидкости некоторая часть работы внешних сил непременно переходит в
тепловую энергию - происходит диссипация энергии. Делением диссипации энергии
на скорость получаем величину, имеющую размерность силы, и которую называют гидродинамическим
сопротивлением. Величина гидродинамического сопротивления в самом общем
случае должна зависеть от размеров и формы потока, от плотности и вязкости жидкости и от поля
скоростей в сечении. Из указанных зависимостей три, а именно: скорость v, линейное измерение потокА l и
коэффициент вязкости ν, объединяются безразмерной величиной
- числом Рейнольдса Re:
![]() (3)
(3)
Установлено,
что гидродинамические сопротивления при ламинарном режиме прямо пропорциональны
первой степени скорости течения, т.е. зависимость будет прямолинейного вида.
Для
турбулентного режима гидродинамические сопротивления будут пропорциональны
квадрату скорости движения, и выражением квадратичного закона сопротивления для
русловых потоков является общеизвестная формула Шези (1).
Процесс
непрерывного перемешивания в турбулентном потоке, естественно, вызывает
появление дополнительного трения между отдельными частицами, которое
оказывается во много десятков раз больше, чем трение при ламинарном режиме.
Задача
исследования сопротивлений и поля скоростей
в турбулентных потоках является гораздо более сложной, чем для
ламинарных потоков. Это объясняется тем многообразием условий, при которых
течение жидкостей происходит при турбулентном режиме, в то время, как
ламинарное течение может наблюдаться при очень ограниченных условиях.
Попытки теоретических исследований закономерностей турбулентного
потока, с целью получения теоретических формул для гидравлических
сопротивлений, делались неоднократно. Одной из таких попыток является теория
Прандтля-Кармана, по которой суммарное напряжение трения в турбулентном потоке
будет иметь вид:
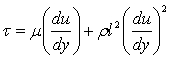
![]() (4)
(4)
При
турбулентном режиме второй член в правой части намного больше первого. Для
ламинарного течения (при малых скоростях) будет преобладать левый член
уравнения.
Строгое
теоретическое определение гидродинамических потерь в трубах является одним из
тех немногих случаев, когда интегрирование дифференциальных уравнений
гидродинамики принципиально возможно и технически осуществимо.
Такой
теоретической формулой, определяющей потери напора при ламинарном режиме в трубах, является формула Пуазейля:
![]() , (5)
, (5)
которая
показывает, что потеря напора при ламинарном режиме пропорциональна первой
степени средней скорости, зависит от рода жидкости (ν),
обратно пропорциональна площади сечения трубы и не зависит от шероховатости
стенок трубы.
Для
турбулентного режима движения в шероховатых трубах Прандтль предложил следующую
формулу:
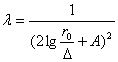 ,
(6)
,
(6)
где: λ
- коэффициент трения,
A - параметр,
характеризующий форму шероховатости, который по опытам Никурадзе для равнозернистой
шероховатости равен А=1,74,
r0- радиус трубы,
Δ - величина выступов отдельных шероховатостей - абсолютная
шероховатость.
Хотя
до недавнего времени формула (6) считалась с теоретической стороны
лучшей, но экспериментальная проверка её показала, что оценка шероховатости только
по высоте выступов недостаточна, а необходимо учитывать также характер расположения
выступов.
Для
изучения зависимости коэффициента трения λ в трубах и лотках от
определяющих его характеристик было проделано много экспериментальных работ,
из которых наиболее значительными были опыты Никурадзе в 1933 г., опыты А.П.
Зегжда в 1938 г. и опыты Ф.А.Шевелева (1953г.).
Никурадзе
исследовал влияние шероховатости на гидравлические сопротивления при конечных
значениях числа Рейнольдса для круглых труб. Он применил искусственную
шероховатость из специально подобранных зерен песка, наклеенных на внутреннюю
поверхность трубы, при этом отношение среднего размера песчинок v радиусу трубы изменялось от 1/507 до 1/15, а число Re , отнесенное к диаметру трубы, доходило до Re =106. Построенный Никурадзе график
зависимости сопротивлений от числа Re и относительной шероховатости Δ/r позволил сделать следующие выводы:
1. При
малых значениях числа Re (менее 2300),
когда весь поток является ламинарным, или в турбулентном потоке ламинарный
подслой имеет толщину, значительно превосходящую размеры выступов
шероховатости, и шероховатость эта не оказывает влияния на сопротивление, λ
зависит только от числа Re
и изображается прямой линией, имеющей уравнение: ![]() (7)
(7)
2. При
средних значениях Re (3,3< lg Re <3,6) выступы шероховатости несколько меньше толщины
ламинарного подслоя, шероховатость уже оказывает влияние на сопротивление,
зависящее в основном от числа Re. Эта
область характеризуется формулами вида: λ=f (Re,![]() ).
).
3. При
больших значениях Re
выступы шероховатости уже полностью
выходят за пределы ламинарного слоя, и сопротивление определяется лишь
степенью шероховатости стенок потока. В этой области - области шероховатых
труб -сопротивление определяется формулами
вида λ=f (![]() ).
).
Можно
также отметить, что чем больше шероховатость, тем раньше наступает
независимость λ от Re , т.е.
вступает в действие квадратичный закон сопротивления.
В 1938
г. А.П.Зегжда опубликовал результаты проведениях им в открытом безнапорном
потоке прямоугольного сечения опытов. В опытах Зегжда применялась также
равнозернистая шероховатость. На полученном им графике видны все режимы
движения жидкостей в каналах, а именно: ламинарное движение, при гладких стенках,
при вполне шероховатых стенках и область перехода от гладких стенок к шероховатым.
Здесь очень
важно отметить, что сходство графиков для круглой трубы (Никурадзе) и для прямоугольного
лотка (Зегжда) имеется как с качественной стороны, так и количественно. Так,
Никурадзе для турбулентного режима предлагает формулу:
![]() (8)
(8)
а
Зегжда для прямоугольного лотка получил:
![]() (9)
(9)
причем
незначительное расхождение в формулах (8) и (9) сам Зегжда относит лить за счет
неточности своих опытов. Таким образом, опытами Зегжда доказана, возможность
использования для открытых русел формул теории турбулентности типа,
примененного для труб.
М.А.Великанов
[2] делает вывод, что: «такое совпадение даёт нам, во-первых, уверенность в правильности
нашего общего подхода к вопросу сопротивления, подхода теоретически не вполне
строгого, и потому нуждающегося в экспериментальном подтверждении, и
во-вторых, совпадение полученных формул до числовых параметров позволяет нам
пользоваться ими и для потоков иных поперечных сечений».
Но при
расчётах сопротивлений все напорные и безнапорные русловые потоки любой формы
сечения обычно заменяют плоским открытым потоком с глубиной, равной гидравлическому
радиусу действительного сечения, с шириной его, равной смоченному периметру, и
стенками, не вызывающими торможения, а эта замена, как отмечает В.Н.Гончаров
[3], не всегда является допустимой. Более того, Гончаров указывает, что:
«множитель С, обычно именуемый коэффициентом Шези, или скоростным коэффициентом,
как это доказано выше, является и должен являться непосредственной функцией
именно формы сечения. Поэтому его целесообразнее было бы именовать параметром формы, выражаемым через отношение к
высоте выступов шероховатости характерного линейного размера сечения,
различного для разных форм сечения».[З]
В
настоящее время установлено, что величина λ и С в самом
общем случае зависят от диаметра (или размеров русла), скорости, абсолютной
шероховатости и характера самой шероховатости, т.е.:
λ = f (d, v, ρ, μ, Δ, A),
где А
- параметр, учитывающий характер
шероховатости.
Помимо
приведенных выше формул, для расчета сопротивлений в трубопроводах существует
ряд других формул (А.Д.Альтшуль,
Г.А.Адамов, Ф.А.Шевелев и др.), но мы их не приводим, так как основной целью
настоящего исследования является обзор формул для определения сопротивлений в
открытых руслах естественных водотоков.
2.
Формулы для определения коэффициента С в
формуле Шези и их сопоставление
В
естественных русловых потоках сопротивления возникают благодаря воздействию на
потоки различного рода факторов, и роль каждого из этих факторов не одинакова.
В.Н.Гончаров [3] классифицирует все виды сопротивлений в руслах
на основные и дополнительные сопротивления. Основными сопротивлениями он
считает «путевые сопротивления потоков, механизм турбулизации которых осуществляется
возмущениями, порождаемыми руслом и формирующими в процессе прохождения ими
толщи потока поле скоростей и режим обмена» [3], а дополнительными - все
факторы, увеличивающие сопротивления сверх основных. К дополнительным
сопротивлениям относятся те сопротивления, которые вызываются массивными
выступами и углублениями, растительностью в русле, изгибами русла, косоструйностью
и водоворотными зонами потока. Практическое значение дополнительных
сопротивлений обусловливается размерами их влияния на общий уровень
сопротивлений.
Все
факторы, вызывающие основные и дополнительные сопротивления, характеризуются
бесконечным разнообразием их форм, размеров и видов. В силу этого почти все
формулы для определения коэффициента С в формуле Шези являются эмпирическими
и зачастую не удовлетворяют тем требованиям, которые предъявляет к ним
практика.
В
нашей стране систематизации гидрометрических материалов о шероховатости
естественных русел начали уделять внимание в достаточной мере лишь после
Октябрьской революции в связи с потребностями широкого дорожного и гидротехнического
строительства. Первая систематизация эмпирических данных о шероховатости была
произведена проф. К.Ф.Срибным, причем по данным Срибного шероховатости в
естественных руслах были значительно больше, чем по данным опытов в каналах и
трубах. Основной же багаж экспериментальных данных гидравлики был накоплен
изучением потоков, дополнительные сопротивления в режиме которых заранее
сводились к возможному минимуму для
получения связи средней скорости именно с основными сопротивлениями. Анализ
вопроса о дополнительных сопротивлениях естественных русловых потоков
выясняет механизм возникновения высоких шероховатостей, встречаемых в практике
при обработке гидрометрических данных.
Все
формулы для определения коэффициента С, предложенные различными
авторами на основе опытных данных, можно разделить на две группы:
1.
Одночленные степенные формулы.
2.
Многочленные формулы.
Вследствие
того, что скоростной коэффициент С имеет размерность квадратного корня
из ускорения ( L1/2 Т-1), при вычислении его следует учитывать,
что формулы для С составлены для метровых мер.
К
первой группе относятся следующие наиболее распространенные формулы:
а)
Формула Маннинга (1890г.):
![]() (10)
(10)
б)
Формула Форхгеймера (1923г.): ![]() (11)
(11)
в) Формула Н.Н. Павловского: 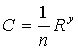 (12)
(12)
В этих
формулах : n - коэффициент шероховатости,
зависящий от состояния поверхности стенок и дна русла;
R - гидравлический радиус сечения.
Наиболее
точной формулой из указанных является
формула (12), предложенная Н.Н.Павловским в 1925 г. и которая явилась как бы
обобщением ранее существовавших показательных формул, поскольку теоретически
было доказано, что показатель степени в формуле для С не может быть постоянным,
а должен зависеть от n. Для определения
показателя степени y по Павловскому им предложена формула:
Y = 2,5 ![]() -0,13-0,75
-0,13-0,75![]() (
(![]() -0,10 ) (13)
-0,10 ) (13)
Так
как при выводе формулы (12) Павловский использовал гидрометрические данные по
каналам при значениях гидравлического радиуса от 0,1 до 3,0 м, то эта формула
применима для открытых русел при значениях 0,1<R<3,0 м. Но, как указывает сам автор формулы (12), «..
.в этом не следует видеть какого-либо специфического ограничения её, так
как данные названной группы опытов не укладываются также и в формулы Маннинга и
Форхгеймера. Последние формулы применяются иногда и при R>3,0 м, но следует признать, что это делается,
собственно, в порядке их экстраполяции за пределы достаточного
экспериментального материала» [7].
Для
приближенных расчётов Павловский предлагает упрощенные формулы:
Y = 1,5 ![]() при 0,1 < R <
1,0 м.
(14)
при 0,1 < R <
1,0 м.
(14)
Y = 1,3 ![]() при 1,0 < R < 3,0 м.
при 1,0 < R < 3,0 м.
В
целях упрощения пользования формулой (12) составлены графики и таблицы y = f (R,n)) и
С =f (R,n) , которые можно найти в каждом справочнике по
гидравлике.
Из
многочленных формул наиболее распространёнными являются:
а/Формула
Гангилье-Куттера (1869 г.):
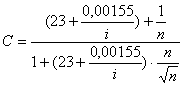 (15)
(15)
Здесь
значение коэффициента шероховатости n - то же,
что и в формулах (10), (11), (12).
При
более значительных уклонах i ≥0,0005 влияние i в формуле незначительно, и формула (15) несколько
сокращается:
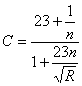 (16)
(16)
Для
пользования формулой составлены достаточно подробные таблицы градаций
коэффициента шероховатости n в
зависимости от состояния русел. [7].
Формула
Гангилье-Куттера даёт достаточно хорошие результаты для естественных
русел и каналов при R
> 3,5м.
б)
Формула Базена (1897г.):
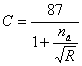 (17)
(17)
где: nб- коэффициент шероховатости по шкале Базена. Для
формулы (17) также была разработана шкала nб, но в настоящее время формула эта почти не
применяется.
в)
Формула А.П.Зегжда, выведенная им из формулы (9):
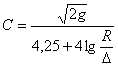 (18)
(18)
где Δ
- значение абсолютной шероховатости (высоты выступов).
Формула
(18), как было сказано выше, была получена по экспериментам в лотке.
Аналогичную зависимость В.Н.Кузнецов получил теоретическим путем.
г) Формула
И.И.Агроскина (1949 г.):
C = 17,72 (k + lgR) ,
(19)
которая
принципиально отличается от предложенных ранее формул тем, что она построена на
рациональной основе, а именно - на использовании зависимости коэффициента
трения λ для открытого турбулентного потока от отношения гидравлического
радиуса к характерному размеру выступов шероховатости Δ : ![]() .
.
Соотношение
между k в формуле (19) и коэффициентом шероховатости n в формулах (10), (11) и (12) равно: k = ![]() .
.
Способ выражения k через n, примененный Агроскиным, нужно объяснять лишь тем,
что к настоящему времени пока ещё отсутствуют данные о фактических величинах
абсолютной шероховатости Δ, соответствующих тем или иным состоянием
русла.
д)
Формулы М.А. Мосткова (1949г.):
Для
движения в области шероховатых русел при развитой турбулентности:
C = 22 lg ![]() + 9,5
+ 9,5![]() +1,5
(20)
+1,5
(20)
Для
движения в области гладких русел, также при развитой турбулентности:
C = 22 lg ![]() - 13,4 (21)
- 13,4 (21)
Мостков
[6] дает таблицу значений высоты влияния выступов шероховатости Δ,
причём последняя по смыслу вывода представляет не геометрический размер выступа,
но учитывает геометрические и
гидравлические характеристики не только отдельных выступов, но и наличие на дне
вымоин, неровностей и т.д.
Все
указанные выше формулы рассчитаны для вычисления средней скорости потока через
коэффициент шероховатости. Некоторыми авторами был предложен целый ряд формул
для определения средней скорости без применения понятия коэффициента
шероховатости (Тейберт, Кристен, Германек, Хессле, Матаневич, Грегер, Виннель,
Тильзен и др.).
Основными
определяющими скорости параметрами в большинстве таких формул приняты: средняя
глубина, уклон, гидравлический радиус и ширина реки. Отличительными особенностями
формул является то, что каждая из них распространяется лишь на отдельные
районы, реки или даже на участки рек.
Например,
формула Тильзена (1933г.) для р. Наровы имеет вид:
V = 2,7 R1,44
I 0,326 (22)
Подобные
же формулы были предложены М.А.Мостковым
[14] в 1938 г. для горных рек Закавказья.
Как
видно из вышеизложенного, для вычисления скоростного коэффициента С
существует очень много формул, поэтому при возникновении необходимости определения
С сразу же встает вопрос, по какой формуле нужно вести его расчет. Как
отмечает Б.В.Поляков, «удачность расчёта С зависит не только от выбора
значения коэффициента (шероховатости), но и от выбора формулы, по которой производится
самый расчёт. При этом более совершенной надо считать такую формулу, которая
даёт значения коэффициентов шероховатости более устойчивые и почти
неизменяющиеся при увеличении наполнения русла и поймы. Это условие очень
важно при расчёте максимальных расходов и кривых подпора, так как оно облегчает
экстраполяцию значений коэффициента шероховатости для высоких горизонтов и
увеличивает точность расчётов». [15].
Наиболее
часто в настоящее время для определения скоростного коэффициента С
используется либо формула
Н.Н.Павловского, либо формула Маннинга, являющаяся частным случаем формулы Павловского
(при n = 1/6 =
0,167). Формула Маннинга широко применяемся за рубежом (особенно в США,
Англии, Индии), сторонники её есть и у нас. Например, этой формулой в своих
работах предпочитает пользоваться В.М.Маккавеев, который считает её наиболее
простой и удачной.
Из
многочленных формул наилучшей для открытого русла является формула Агроскина.
Её же настоятельно рекомендует
Н.Н.Федоров. [17].
Сравнение
формул на графике в логарифмическом масштабе (см.Прилож.1) показало, что для одних
и тех же величин коэффициента шероховатости значение С по формулам
Маннинга и Гангилье-Куттера для R
< 1,0 м получаются в сравнении с формулой Павловского заниженными для
малых коэффициентов шероховатостей и завышенными - для n >
0,020. Для R >1,0 м. расположение
кривых, характеризующих каждую формулу, обратное, чем для R <1,0; при R = 1,0 м
кривые пересекаются в одной точке.
Формула
Агроскина для небольших водотоков даёт заниженные величины С в
сравнении с формулой Павловского.
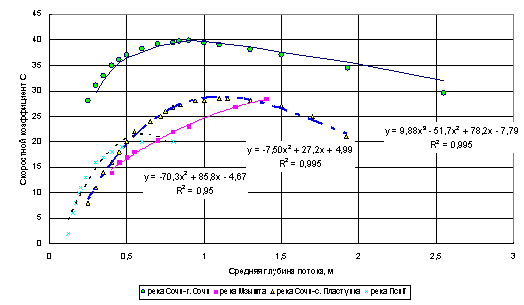
Нанесенные
на графике эмпирические точки (С, hср), полученные
по гидрометрическим данным поста р.Сочи-с.Пластунка (за период 1947-1960 гг.)
дают кривую связи С=f (hср), совершенно
отличную от кривых взятых формул. Зависимость С=f (hср) имеет вид параболы, пересекающей семейство кривых С= f (R, n); поэтому можно сказать, что входящие в формулы для С
коэффициенты, характеризующие шероховатость русла, для естественных русел
изменяются весьма значительно, какую бы формулу для расчетов С мы ни взяли.
Весь вопрос упирается в необходимость выбора наиболее подходящего для данной
формулы коэффициента шероховатости, чтобы получить наиболее правильной значение
скоростного коэффициента.
3. Динамика коэффициента шероховатости по
данным
гидрометрических измерений на некоторых горных реках Кавказа
При
определении средних скоростей в сечении для естественных русел по формулам
Шези и Павловского в настоящее время коэффициент шероховатости назначают или по
таблице М.Ф.Срибного, или же по данным натурных измерений.
В
таблице М.Ф.Срибного приведена достаточно подробная характеристика видов русел
и соответствующие каждому виду коэффициенты шероховатости, однако таблица эта является
очень грубой схемой и не учитывает динамики коэффициента шероховатости. Как
отмечал ещё в 1936 г. Б.В.Поляков, «значения коэффициентов шероховатости не
могут умещаться в каких-либо тесных рамках таблиц. Для данного состояния
шероховатости необходимо давать достаточно широкие пределы. Эти пределы также
не являются строгими, неподвижными. Поэтому пользование таблицами для
нахождения С влечёт за собой частые ошибки. Для уменьшения их при ответственных
проектах необходимы исследования в натуре».[15]
Для
того, чтобы назначать коэффициент шероховатости (КШ) на основании опытных
данных, необходимо знать, как изменяется коэффициент шероховатости, его
динамику. Проф. А.Н.Ахутин в 1931 г. писал: «Необходимо также более внимательно
исследовать саму природу того фактора, который мы называем КШ. Истинное значение
КШ еще не вполне выяснено. Изучение имеющегося материала позволяет утверждать,
что КШ меняется с глубиной (с гидравлическим радиусом), с видом (степенью шероховатости)
русла, но и с уклоном, с изменением живого сечения русла и потока в плане». [1]
Таким
образом, картина динамики КШ оказывается гораздо более сложной, чем кажется на
первый взгляд.
С
целью выяснения характера изменения коэффициента шероховатости в условиях
естественных русел горных рек нами была произведена обработка гидрометрических
данных по 10 створам, расположенным на горных реках юго-западного склона
Кавказа. Обработка состояла в вычислении по измерениям расходов воды скоростных
коэффициентов ( С= ![]() ) и коэффициентов
шероховатости (по Павловскому: п=
) и коэффициентов
шероховатости (по Павловскому: п=![]() , а затем - в построении зависимостей n=f(vср) и n=f(hср.·i). Вместо
величин гидравлического радиуса при этом брались средние глубины потока,
полученные делением площади сечения на ширину, поскольку от такой замены
вносимая в расчеты ошибка не превышала 1-3%.
, а затем - в построении зависимостей n=f(vср) и n=f(hср.·i). Вместо
величин гидравлического радиуса при этом брались средние глубины потока,
полученные делением площади сечения на ширину, поскольку от такой замены
вносимая в расчеты ошибка не превышала 1-3%.
При
определении коэффициента шероховатости по формуле Павловского значение
показателя степени y бралось по формуле (13).
В
целях облегчения весьма трудоемких подсчетов при вычислении КШ был построен
график зависимости n=f(C=![]() , R) (по вертикальной оси графика – n, по горизонтальной
- С, каждая кривая на графике - для определенного R, который менялся от 0,05 до 5 м), а затем по графику
была составлена расчётная таблица. Таким образом, коэффициент шероховатости
определялся по расчётной таблице по вычисленному C=
, R) (по вертикальной оси графика – n, по горизонтальной
- С, каждая кривая на графике - для определенного R, который менялся от 0,05 до 5 м), а затем по графику
была составлена расчётная таблица. Таким образом, коэффициент шероховатости
определялся по расчётной таблице по вычисленному C=![]() , и
hср.
, и
hср.
Всего
было обработано 1541 измерение расхода воды вертушкой; результаты
вычислений в настоящей статье представлены графически в виде зависимостей n=f(vср) (см. Прилож.2-10). Рассмотрим полученные данные по
каждому посту отдельно.
1.
Гидрометрический пост р.Псезуапсе-с.Татьяновка
Гидрометрический
створ расположен на прямолинейном участке, русло сложено галечниковыми отложениями,
поперечный профиль имеет плавное параболическое очертание. Уклоны измеряются на
участке: верхний уклонный пост, расположенный в 80,7 м от основного водпоста,
- основной водпост, который
совмещен с гидроствором.
Коэффициент
шероховатости вычислен по 51 измерению расхода воды (1959 - I960 гг.), охватывающих
амплитуды: vср
=0,11 —2,78 м/сек, hср=0,30 —1,49 м, Q =1,22 - 130 м3/c. Уклоны водной поверхности изменялись от i=4,3%0 при высоких уровнях до i=1,2%0 - при низких уровнях.
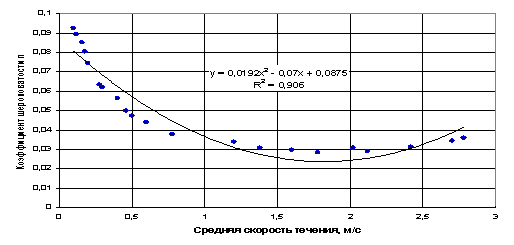
Как
видно из построенного графика n=f(vср) (см.Прилож.1), КШ уменьшался от 0,092 при малых
глубинах и скоростях до 0,026 при vср=1,6 - 2,0 м/сек, а затем – с увеличением скоростей -
несколько повышался (до n
=0,026). Отклонения точек от усредняющей кривой не превышают ±13%.
2.
Гидрометрический пост р. Шахе -с. Солох-Аул
Гидроствор
расположен в среднем течении реки, пойма на участке поста отсутствует, и галечниковое
русло располагается между крутыми склонами долины, ширина которой по
дну составляет 60 м. Деформация на участке гидроствора весьма значительная,
русло блуждающее. Вследствие влияния движущихся перекатов часто наблюдается
косоструйность в гидростворе.
Уклоны
измеряются по НУП и ВУП, расстояние между которыми 54 м.
В
результате обработки расходов воды,
измеренных в период 1956 - 1960 гг., получено 268 значений КШ, которые
соответствуют амплитудам vср
=0,37—2,77 м/сек, hср =0,22-1,75 м,
Q =3,37 —155 м3/c, i=0,19—17%о.
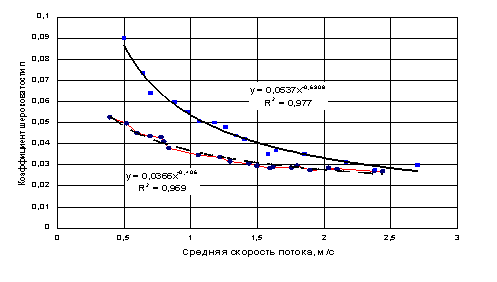
Как видно на графике n=f(vср) (см.Прилож.2), КШ
изменяется от 0,019 до 0,090, график этот характеризуется весьма большим
разбросом точек, достигающим 50% величины n, при этом
достаточно четко вырисовываются две кривых, соответствующих двум различным положениям
русла реки в плане. В правой части графика при больших глубинах и скоростях разброс
точек меньше, и кривые сближаются.
З. Гидрометрический пост р.Псий-с.Тух-Аул
Гидроствор
расположен на прямолинейном участке, русло сложено гравелистыми отложениями со значительной долей булыжников и
валунов, в паводки деформируется.
Уклоны
измеряются по уклонным постам, расстояние между которыми 60 м.
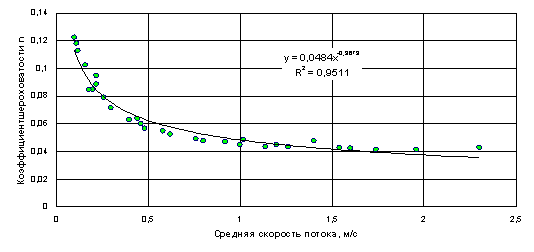
КШ
вычислены по 253 измерениям расхода воды (за период 1956 — I960 гг.),
освещающим амлитуды колебаний: vср=
0,11-2,48 м/с, hср =0,12 —0,80 м, Q=0,055 -22,8 м3/c, i =14— 22 %о . Амплитуда изменений КШ
п =0,122 - 0,033. Точки на графике n=f(vср) (см. Прилож.3) имеют большой разброс с
максимальным отклонением от осредняющей их кривой до ±27%.
4.
Гидрометрический пост р.Сочи - с.Пластунка
Гидроствор
расположен на прямолинейном участке, русло правильной формы, деформации его
сравнительно невелики. Уклоны измеряются по уклонным постам, расстояние между
которыми 73 м.
В
результате обработки 265 расходов воды, измеренных в период 1947 - I960 гг. и
освещающих амплитуду колебаний vср
=0,22 - 2,84 м/с, hср
=0,24 — 2,02 м, Q = 1,44-301 м3/c, i =1,9-7,2 %о,
получены величины коэффициента шероховатости в пределах п =0,068 — 0,031.
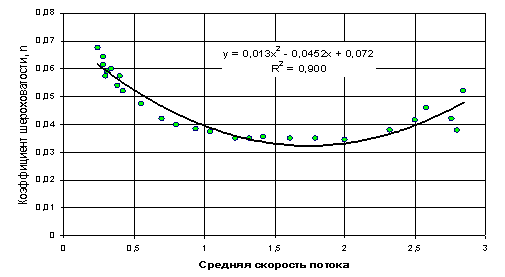
Точки
на графике n=f(vср) (см. Прилож.4)
располагаются сравнительно неширокой полосой, укладываясь в подавляющем
большинстве своем в 10%-ную полосу рассеяния и очень чётко выявляя параболический
вид кривой n=f(vср) с минимумом при vср
=l,4 -1,8 м/сек. График n=f(hср) даёт примерно такой же
вид кривой и с такими же отклонениями точек.
5. Гидрометрический
пост р. Сочи - г.Сочи
Гидроствор
№l располагался на приустьевом участке реки,
подверженном периодическим подпорам от приустьевого бара и уровня моря. Река на
этом участке имеет бетонную опояску берегов и дно в естественном состоянии.
Вычисленные
115 значений п дают на графике очень большой разброс точек ( п
, vср
) (см.Прилож.5)
Для
гидроствора №2, расположенного вне зоны подпора и имеющего более устойчивый
профиль, точки ( п, vср
) ложатся гораздо более тесной группой. КШ здесь имеют небольшую амплитуду
изменений (0,039 - 0,019) и устойчивые низкие величины при средних глубинах (
п =0,022).

Рис. 2. Гидроствор поста р.Шахе - с.Солох-Аул, август 1961 г.
6. Гидрометрический
пост р. Мзымта - р. п.
Красная Поляна
Русло
на участке гидроствора имеет слабый изгиб, сложено галечником и валунами.
Уклоны измеряются по уклонным постам, расположенным на расстоянии 138 м.
За
период наблюдений 1948,1956-1960 гг. по измерениям расхода воды было вычислено
220 значений КШ, которые соответствуют изменениям vср
=0,67—3,17 м/с, hср=0,29—1,32м, Q =7,58 -214 м3/с
и i =5,1 - 9,5 %о. При этом значения КШ расположились в
пределах п =0,059— 0,036.
Точки ( п , vср ) на графике
(см. Прилож.6) дают сравнительно небольшое рассеяние - до ±15-10% от средней кривой. Зависимость n=f(hср·i) имеет такой же вид , как и n=f(hср).
7. Гидрометрический пост р.Мзымта-пос.Кепш
Гидроствор
расположен на участке, где река прорезает
хребет Ах-Цу, поэтому Мзымта в этом месте имеет большие уклоны, скорости и
глубины при сравнительно небольшой глубине потока. Русло изобилует большими
валунами, много осыпей. Верхний уклонный пост расположен в 80 м выше основного
водпоста, последний служит нижним уклонным постом.
По
данным этого поста было вычислено 142 значения коэффициента шероховатости
при vср
=0,54- 3,22 м/с, hср
=0,98—2,77 м, Q, =11,4 -2.56 м3/с . Наименьшая величина
п =0,048, а наибольшая - п =0,089. Точки ( п , vср
) расположились на графике (см.
Прилож.7) разбросанно (при отклонениях до ±20% , но все же отчётливо
образуют параболу с минимумом
при vср
=1,8 - 2,2 м/с.
8. Гидрометрические посты р.Бешенка-р.п.Красная
Поляна и р. Кепш-пос.Кепш
Это
небольшие горные водотоки, характеризующиеся огромными уклонами (у р.Бешенки i =51 —61 %о, у р.Кепш - i =13 - 23 %o) и валунным типом русел.
КШ для них получены очень большими - до п
=0,127 (см. Прилож.8).
9. Полученные данные по КШ для р.Теребля у с.Колочава
- небольшой горной реки Западной Украины (см. Прилож.9) показывают, что
аналогичный вышеуказанным вид имеют зависимости n=f(vср) и для других рек.
Совмещенные
на одном графике кривые связи n=f(vср) показывают, что:
а) все
кривые имеют вид параболы различной формы (иногда - довольно сложной),
смещенных относительно друг друга по вертикали, и в меньшей степени - по
горизонтали;
б) для
каждого створа отчетливо видна левая ветвь параболы, т.е. увеличение
шероховатости при уменьшении глубин для меженных расходов;
в)
минимальные значения на каждой из
парабол смещаются вправо с увеличением высоты её расположения; так, если для
створа р.Сочи-г.Сочи минимум n=0,022 при vср=1,4 м/с, то для створа р.Мзымта-пос.Кепш n
=0,058 при vср
=2,0 м/с;
г)
правая ветвь параболы не для всех створов ясно выражена - вероятно, за счёт
недостаточности по количеству измеренных расходов воды.
Таким
образом, коэффициенты шероховатости для горных рек оказываются весьма
динамичными и изменяются в больших пределах, что является причиной очень
больших ошибок при вычислении максимальных расходов воды по формуле Шези, в
особенности - при определении КШ по таблице Срибного,

Рис.
3. Участок водпоста р.Мзымта-пос.Кепш. Октябрь 1961г.
Основными
факторами, влияющими на динамику КШ, являются: размер и характер расположения
выступов дна, форма русла, глубина и уклон. Все эти факторы и определяют форму
кривых связи n=f(hср) и n=f(vср) . Разумеется, чем
больше деформация русла, тем больше разброс точек на графиках связи n=f(vср), что можно видеть и по
прилагаемым зависимостям: для створа с наименьшей деформацией (р.Сочи-с.
Пластунка) точки ( n, vср
) имеют минимальный разброс, а для створа с наибольшем деформацией
(р.Шахе-с.Солох-Аул)-максимальный.
При
этом следует отметить, что рассеяние точек имеет определенный предел, различный
для разных створов. Минимальное значение
при vср =1,4 - 2,0 м/с
коэффициента шероховатости указывает на то, что каждое русло при
каком-то среднем для данной реки расходе воды имеет наибольшую пропускную
способность, больше и меньше которого пропускная способность уменьшается. Этот оптимальный
расход будет, очевидно, руслообразующим. Для расходов, меньших руслообразующего,
КШ увеличивается за счет увеличения относительной шероховатости Δ/h (при атом высота
выступов и их расположение, т.е. рельеф шероховатости - будет неизменным). Для
расходов, больших руслообразующего
расхода, увеличение КШ связано с увеличением насыщенности водного потока
влекомыми и взвешенными
наносами - при достаточно больших скоростях теряется четкая граница
между потоком и дном. Помимо этого фактора не следует также забывать и о том,
что в большинстве случаев с ростом уровня воды увеличивается и тормозящее
влияние пологих берегов и поймы.
О
влиянии влекомых наносов на динамику КШ писал Б.В.Поляков: «В отношении второго
фактора необходимо указать, что подобно тому, как значительное увеличение
мутности потока влечёт за собой уменьшение скорости движения потока, так и
увеличение влечения донных наносов несомненно, изменяет условия трения в пограничном
слое. Шоклич нашёл, что при прочих равных условиях расход в опытном лотке при
подвижном дне меньше, чем при неподвижном, т.е. фиксирование донных частиц освобождает
известное количество энергии, идущее на увеличение расхода. Очевидно, что поток,
имеющий большое количество донных наносов, даёт более шероховатое
соприкосновение с ложем».[15]
Проф.
Вызго была построена обобщённая для некоторых рек Средней Азии зависимость n=f (Q).
Касаясь вида этого графика, Вызго пишет: «Значения коэффициента шероховатости
меньше в условиях устойчивого состояния, при движении донных наносов, и
увеличиваются с уменьшением расхода и с прекращением движения наносов.
Некоторое увеличение "кш" наблюдается при увеличении расхода...»
[13]. Вероятно, построение графика n=f (Q), обобщенного для нескольких рек, было произведено для
таких рек, которые были примерно одинаковы по условиям протекания и по своей
водности. Как показали приводимые здесь графики, для различных рек, и даже для
участков рек, нельзя построить общей зависимости n=f(vср).
Проф.А.Н.Ахутин
отмечает несколько другие причины увеличения коэффициента шероховатости:
«Вместе с тем замечено, что при увеличении глубины свыше известного предела
значение КШ снова может возрастать, причём это возрастание объясняется не
только увеличением шероховатости в верхних заросших травой и кустарником частях
русла или растеканием воды по поймам, но и увеличением при высокой воде степени
неравномерности течения воды». [1]
Очень
интересны следующие его указания: «Замечено также, что при резком чередовании
перекатов и глубоких плёсов значения КШ получаются несколько искаженными.
Очевидно, на величину КШ влияет каким-то образом наличие верхнего, а иногда,
наоборот, нижнего участка, резко отличным характером течения».
Эти
последние обстоятельства дают некоторое основание утверждать, что для
вычисления КШ во многих (если не во всех) случаях следует пользоваться не уравнением
равномерного движения (Шези), а основным уравнением неравномерного движения,
учитывающим изменения скоростей при переходе от одного сечения к другому. Лучше
всего для этой цели может служить уравнение:
![]() , (23)
, (23)
в
котором v1 , v2 , и i измеряются
непосредственно на месте; v и R вычисляются как средние значения на данном участке."
[1]
Исходя
из анализа обработанных натурных данных по КШ, можно сделать ещё один вывод:
чем большим запасом кинетической энергии обладает поток, тем большее её
количество этот поток (в естественном состоянии) должен затратить на преодоление
путевых сопротивлений, т.е. тем больше КШ. Это объясняется взаимодействием
потока с руслом: увеличение скоростей резко повышает транспортирующую способность
потока. По тем же причинам коэффициенты шероховатости будут больше для перекатов,
чем для плёсовых участков рек, должно также наблюдаться уменьшение КШ от истока
к устью реки. Интересно отметить, что для зарегулированной реки (устроены
бетонные береговые стенки - гидроствор р.Сочи - г.Сочи) коэффициенты
шероховатости оказались наименьшими в сравнении с другими – незарегулированными
- реками. '
Выводы
На
основании проведенного анализа можно сделать следующие выводы:
1. При
определении скоростного коэффициента для формулы Шези следует пользоваться формулами
Павловского или Агроскина, поскольку указанные формулы дают наиболее надёжные
результаты по сравнении с другими.
2.
Выбор коэффициента шероховатости по таблице Срибного на основании характеристик
водного потока обладает тем недостатком, что в оценку n
вносится элемент субъективности, что может привести к большим ошибкам в
расчётах. Помимо этого, при таком выборе не учитывается динамика коэффициента
шероховатости.
3.
Коэффициент шероховатости можно с достаточной степенью точности определять по
построенным на основании гидрометрических данных зависимостям n=f(hср) или n=f(H) .для рек с небольшой деформацией русла.
4.Как
показала обработка опытных данных, коэффициент шероховатости для горных рек
может изменяться в значительных пределах, увеличиваясь до n=0,100
- 0,127 при малых расходах и до n=0,050
- 0,070 - при паводочных расходах, и уменьшаясь до n=0,022
- 0,042 при средних расходах. По своей динамичности коэффициент шероховатости
почти одинаков со скоростным
коэффициентом. Так, для створа р.Сочи-с.Пластунка отношение ![]() а
а ![]()
5.
В связи с разработкой формул для С
с введением характеристики абсолютной шероховатости, наиболее достоверным
способом оценки шероховатости естественного русла может быть установление его
абсолютной шероховатости путём непосредственного измерения характерных
неровностей дна или путём стереофотосъёмки.
Литература:
1.Ахутин
А.Н. Неравномерное движение воды в открытых руслах. ОГИЗ. М-Л, 1931.
2. Великанов М.А.Динамика русловых
потоков. Гидрометеоиздат. Л,1949.
З. Гончаров
В.И. Основы динамики русловых потоков. Гидрометеоиздат. Л, 1954.
4. Горбачев А.И. Гидравлика. Гос.
транспортное изд-во. М-Л, 1933.
5.Латышенков А.М., Лобачев В.Г.
Гидравлика. Гос.изд-во литературы по строительству и архитектуре. М.,
1956.
6. Мостков М.А. Гидравлический
справочник. Гос. изд-во литературы по строительству и архитектуре. М.,1954.
7. Павловский
Н.Н. Учебный гидравлический справочник, ОНТИ. Л,1932.
8. Рабинович
Е.З. Гидравлика. Гос. изд-во технико-теоретической литературы, М,1956.
9. Чеботарев
А.И. Общая гидрология. Гидрометеоиздат.Л.1960.
10. Чертоусов
М.Д. Гидравлика. Специальный курс. Госэнергетическое изд-во. М-Л, 1957.
11. Шамов
Г.И. Речные наносы. Гидрометеоиздат.Л,1959.
12.Яблонский
B.C. Гидравлика. Гостоптехиздат.М,1957.
Журнальные
статьи
13.Вызго
М.С. О коэффициенте шероховатости. Гидротехническое строительство, 11,
1951.
14. Мостков
М.А. Расчетная формула для горных потоков, находящихся в естественном
состоянии. Метеорология и гидрология, №5,
1938
15. Поляков
Б.В. Значение коэффициента шероховатости русел и пойм равнинных рек. Метеорология
и гидрология, №12, 1936.
16.Стащук
И.Г. Об использовании в гидрометрии некоторых гидравлических свойств
открытых русел. Метеорология и гидрология, №8. 1937
17.Федоров
Н.Н.Об определении скоростного множителя С для естественных русел. Труды
ГГИ,вып.56(110), 1956.
Приложение 1
Зависимость коэффициента шероховатости от средней скорости потока. Р.Псезуапсе – с. Татьяновка, 1959-1960 гг.
Приложение 2
Зависимость коэффициента шероховатости от средней скорости потока. Р.Шахе – с. Солох-Аул, 1956-1960 гг.
Приложение 3
Зависимость коэффициента
шероховатости от средней скорости потока. Р.Псий – с. Тух-Аул
Приложение 4
Зависимость коэффициента шероховатости от средней скорости потока.
Р.Сочи – с. Пластунка
Приложение 5
Зависимость коэффициента шероховатости от средней скорости потока.
Р.Мзымта – р. п. Красная Поляна
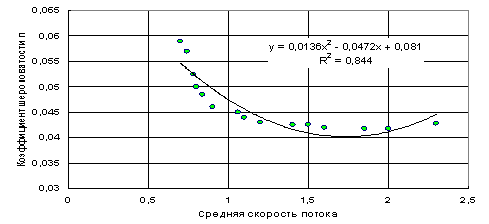
Приложение 6
Зависимость коэффициента шероховатости от средней скорости потока.
Р.Мзымта – пос.
Кепш
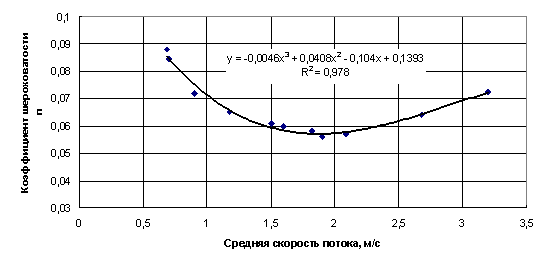
Приложение 7
Зависимость коэффициента шероховатости от средней скорости потока.
Р.Бешенка –
р.п.Красная Поляна, р.Кепш - пос. Кепш
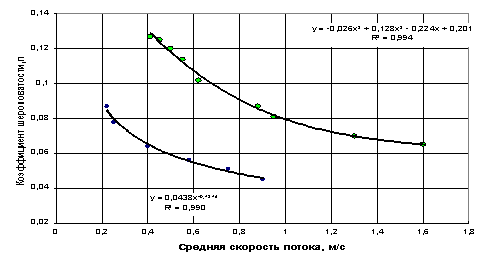
Приложение 8
Зависимость коэффициента шероховатости от средней скорости потока.
Р.Теребля –
с.Колочава
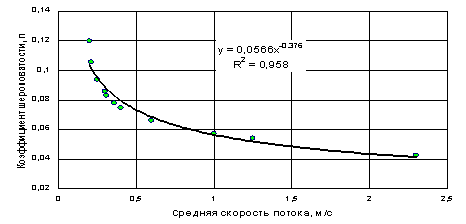
Приложение 9
Зависимость скоростного коэффициента от средней глубины потока.