Математика/ 1.Дифференциальные и
интегральные
уравнения.
К.ф.-м. н., доцент Ысмагул Р.С.
Студент спец. «Математика» Титова А.А.
Костанайский государственный университет
им. А.Байтурсынова, Казахстан
Применение метода укорочения для построения почти многопериодического
решения ![]() -систем
-систем
Рассмотрим систему
интегро-дифференциальных уравнений вида
[1]
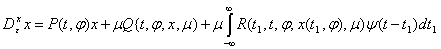 ,
(1)
,
(1)
и укороченное
по ![]() уравнение
уравнение
![]() , (2)
, (2)
где ![]() -
- ![]() -векторы;
-векторы; ![]() - счетномерный
вектор,
- счетномерный
вектор,
![]()
есть укороченный дифференциальный оператор.
Пусть ![]() . Тогда
. Тогда ![]() .
.
Мы знаем, что
![]() .
.
Пусть ![]() - характеристическая
функция оператора
- характеристическая
функция оператора ![]() и удовлетворяет
интегральному уравнению
и удовлетворяет
интегральному уравнению
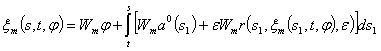 .
.
Пусть для линеаризованного однородного уравнения
![]() (3)
(3)
существует матрица типа Грина ![]() , удовлетворяющая условию
, удовлетворяющая условию
![]() (4)
(4)
с постоянными ![]() ,
, ![]() для всех
для всех ![]() , где
, где ![]() - достаточно большое натуральное число.
- достаточно большое натуральное число.
Лемма . Если выполнены условия ![]() для
для ![]() и
и ![]() и условие (4), то при
и условие (4), то при
![]() и конечных
фиксированных значениях
и конечных
фиксированных значениях ![]() последовательность
последовательность ![]() сходится по
норме к матрице
сходится по
норме к матрице ![]() типа Грина для
уравнения
типа Грина для
уравнения ![]() , причем
, причем
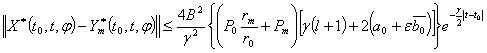
![]() .
.
Теорема. Пусть относительно величин ![]() ,
, ![]() и
и ![]() выполняются
условия
выполняются
условия ![]() и пусть уравнение (3)
имеет матрицу типа Грина, удовлетворяющую условию (4). Тогда можно указать
и пусть уравнение (3)
имеет матрицу типа Грина, удовлетворяющую условию (4). Тогда можно указать ![]() и
и ![]() такие, что при
такие, что при ![]() ,
, ![]() уравнение (2) допускает
единственное п.м.п.
уравнение (2) допускает
единственное п.м.п. ![]() -решение
-решение ![]() , причем
, причем
![]()
в смысле сходимости по норме.
Доказательство. Из выполнения условий ![]() и (4) на основании теоремы следует, что
уравнение (2) при
и (4) на основании теоремы следует, что
уравнение (2) при ![]() ,
, ![]() имеет единственное
п.м.п. решение. Обозначим его через
имеет единственное
п.м.п. решение. Обозначим его через ![]() , опуская зависимость от параметров
, опуская зависимость от параметров ![]() и
и ![]() . Это решение удовлетворяет интегральному уравнению
. Это решение удовлетворяет интегральному уравнению
![]() .
.
Пользуясь усиленным условием Липшица [2], можно
записать
![]() .
.
С другой
стороны, вектор-функция ![]() п.м.п., поэтому имеем
п.м.п., поэтому имеем
![]() .
.
Теперь с учетом оценки (4) будем иметь
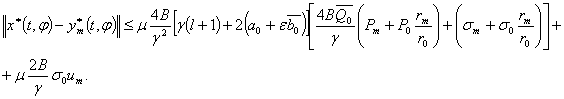
Если ![]() и
и ![]() , то
, то
![]() . (5)
. (5)
Из (4) ясно,
что при ![]() имеем
имеем ![]() . Тогда из (5) следует, что
. Тогда из (5) следует, что
![]()
при ![]() . Следовательно,
. Следовательно,
![]()
равномерно по ![]() . Теорема доказана.
. Теорема доказана.
Литература:
1 Умбетжанов Д.У. Почти периодические
решения дифференциальных уравнений в
частных поризводных. -Алма-Ата: Наука,
1979. - 188 с.
2 Жаутыков О.А. Счетные системы
дифференциальных уравнений и их применение./Дифференциальное уравнение. Т.I, №2.-Алма-Ата,1965.С.16-17.