Математика/1. Дифференциальные и интегральные уравнения

к.т.н. Бутенков С.А.¹, Нагоров А.Л.²

¹Технологический институт Южного федерального университета в г. Таганроге, Россия

²Кабардино-Балкарский государственный университет им. Х.М. Бербекова, Россия

Проектирование численных методов решения уравнений на гранулированных моделях сред

В связи с развитием высокопроизводительных вычислительных систем в настоящее время встает задача унификации вычислительных процессов и структур с целью упрощения проектирования и оценки алгоритмов и аппаратных средств численных расчетов (ценной некоторой потери точности и производительности). Взамен мы получаем прозрачность, простоту построения, соответствие реальности [1]. Это все является целью обширной программы работ в области теории информационной грануляции, развиваемой L. Zadeh [2]. Потребителем таких разработок, являются, в частности, системы облачных вычислений (cloud computing). Именно они требуют применения массивно параллельных, масштабируемых и максимально унифицированных вычислительных средств [3].

Решение этой проблемы может быть найдено с помощью общей теории грануляции, развитой в ряде наших работ [4-7] на общей основе принципа мягких вычислений, введенного L. Zadeh. Полученные результаты в области алгебраизации методов гранулированных вычислений [7] обобщают предложенное L. Zadeh понятие грануляции на многомерный случай и вводят методологию грануляции многомерных данных [8,9]. Согласно этим работам, возможен единый подход к гранулированному обобщению основных математических понятий переменной, функции и отношения, который приводит к основным понятиям гранулированного моделирования (Рис. 1).

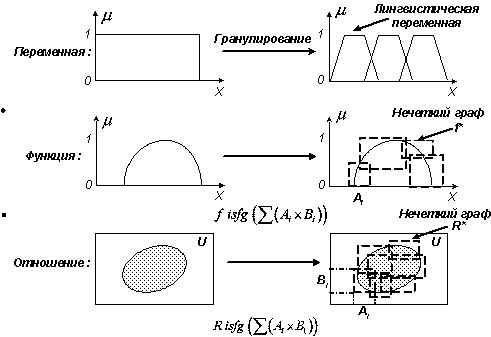
Рис. 1. Гранулирование основных математических понятий: переменной, функции и отношения по [2,5].

Развитие математического аппарата пространственной грануляции позволило получить ряд новых математических моделей, в частности, в области моделирования фрактальных сред [6-8]. Однако новые модели математической физики опираются в прикладной части на известные численные методы моделирования. В настоящей работе предлагается взгляд на известные методы с точки зрения теории грануляции, что позволяет ввести новые формы представления численных методов в арсенал гранулированных моделей и вычислений на них.

Рассмотрим классическую задачу приближенного вычисления интегралов [9]. Интервал интегрирования делится на отрезков, образуя узлы, в которых известны значения подынтегральной функции. В курсе численных методов рассматривается задача на сетке с равномерно заданными узлами , . Применяя формулу Тейлора, получают квадратурные формулы вида:

, (1)

где – коэффициенты, зависящие только от выбора узлов сетки, но не от вида подынтегральной функции, а – остаточный член, определяющий погрешность усечения квадратурной формулы (1). Выбор узлов в случае гранулированного подхода определяется исходной моделью объекта, например, представленной в гранулированной форме [6].

В терминологии ТИГ модели Рис. 1 инкапсулируют сверху и снизу криволинейную трапецию, образуемую графиком подынтегральной функции на заданном интервале. На этой модели введены общие выражения спектра мер на гранулах [5]. Три базовые меры на плоской грануле , имеющие очевидный геометрический смысл, задаются в виде:

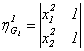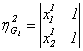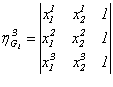, ,. (2)

Значение дает величину правого (левого) приближения для подынтегральной функции на интервале, что позволяет ввести аналоги квадратурных формул (1) на моделях (2). Используя алгебраичность моделей (2), можно получить компактные представления для основных квадратурных формул на основе (2). Так, для формулы правых прямоугольников получаем следующее компактное выражение для всего гранулирования отрезка интегрирования на основе (2):

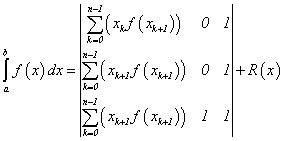. (3)

Соответственно, для формулы левых прямоугольников:

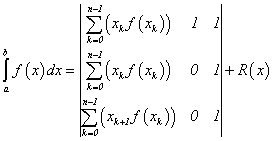. (4)

Квадратурные формулы прямоугольников на гранулах (3),(4) имеют первый порядок точности [1] и требуют вычислений подынтегральной функции в узлах. Их важнейшим преимуществом является применимость в случае, когда узлы сетки заданы неравномерно (моделями гранул [6]). Повысить точность квадратурных формул можно путем введения формулы средних прямоугольников на гранулированном представлении интервала интегрирования в виде:

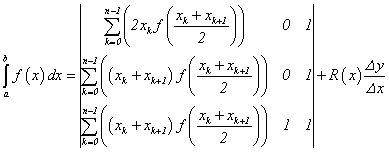. (5)

Как и классическая формула средних прямоугольников, формула (5) имеет порядок точности не хуже второго [1]. Использование общих квадратурных формул на гранулах позволяет развивать технику построения специализированных систем гранулированных вычислений применительно к задачам математической физики. В частности, в [10] предложена общая структура систем гранулированных вычислений, реализующая парадигму мягких вычислений по L. Zadeh [2]. В результате применения структуры гранулирующего вычислителя и разработанных для него численных методов удается предельно типизировать структуру вычислительных устройств для решения ряда задач математической физики [6]. Введенная методология и структура вычислителя допускают также массивное распараллеливание вычислительного процесса (например, за счет применения нейронных сетей, решающих задачи (3)-(5). Машина гранулированных вычислений в этом случае имеет типовую структуру для реализации облачных вычислений, возможно – параллельно для каждой гранулы. На выходе происходит «сборка» полученного значения приближенной квадратуры.

Литература

1. Кречетов Н.. Продукты для интеллектуального анализа данных. – Рынок программных средств, № 14–15, 1997, c. 32–39.

2. Zadeh L. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic // Fuzzy Sets and Systems, vol. 90, p. 111–127, 1997.

3. Gillam L. Cloud Computing: Principles, Systems and Applications / N. Antonopoulos, L. Gillam.– L.: Springer, 2010.– 379 p.

4. Butenkov S., Krivsha V., Al Dhouyani S. Granular Computing in Computer Image Perception: basic issues and Glass Box models. // In Proc. IASTED Conf. “AIA 2006”, Innsbruk, Austria, February 16-18 2006, pp. 811-816.

5. Бутенков С.А. Алгебраические модели в задачах интеллектуального анализа многомерных данных // Сб. трудов международной конференции “Математическая теория систем 2009”, Москва, 26-30 января 2009, c. 93-101.

6. Бутенков С.А., Жуков А.Л. Общая модель фрактального объекта для различной размерности вмещающего пространства // Материалы Второго Международного Российско-Казахского симпозиума “Уравнения смешанного типа и родственные проблемы анализа и информатики”.– Нальчик, 23‑27 мая 2011 г., с. 48‑51.

7. Бутенков С.А., Жуков А.Л. Информационная грануляция на основе изоморфизма алгебраических систем // Сборник трудов международной алгебраической конференции, посвященной 80-летию со дня рождения А.И. Кострикина. Нальчик, 12‑18 июля 2009 г., с. 106‑113.

8. Нагоров А.Л. Интеллектуализация моделирования физических процессов переноса // В сб. трудов Конгресса по интеллектуальным технологиям IS-IT’12, т. 3, М.:ФИЗМАТЛИТ, 2012, с. 234-239.

9. Бутенков С.А. Развитие парадигмы интеллектуального анализа многомерной информации применительно к теории информационной грануляции // В сб. трудов IV Международного научно-практического семинара “Интегрированные модели и мягкие вычисления в искусственном интеллекте”, Коломна, 28-30 мая 2007 г., т.1, с. 188-194.

10. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для вузов.– М.: Наука. Гл. ред. Физико-математической литературы, 1989, 432 стр.