С.И. Куликов, А.И. Нестеренко,
Н.Г. Нестеренко
Математическая модель распределения плотности тока в сплошном
цилиндрическом нагревателе камеры высокого давления
ГВУЗ “ Украинский
государственный химико-технологический университет”
г. Днепропетровск
Для создания высокой температуры в камерах
высокого давления широко используется прямой нагрев смеси методом
сопротивления. При этом характер распределения температуры определяется в
основном интенсивностью тепловыделения при прохождении электрического тока.
Рассмотрим
распределение плотности переменного тока в сплошном цилиндрическом нагревателе
камеры высокого давления. Распределение электромагнитного поля в среде описывается системой уравнений Максвелла [1]:
![]()
![]() , (1)
, (1)
где ![]() - вектора напряжённости магнитного и электрического
поля соответственно;
- вектора напряжённости магнитного и электрического
поля соответственно;
![]() - вектор плотности
тока;
- вектор плотности
тока; ![]() - магнитная
проницаемость среды;
- магнитная
проницаемость среды; ![]() - частота;
- частота; ![]() - мнимая единица.
- мнимая единица.
Для
осевой симметрии имеем:
![]()
![]() (2)
(2)
Используя запись закона Ома в дифференциальной форме,
![]()
а также, переходя к цилиндрическим координатам,
преобразуем систему (1) к виду:
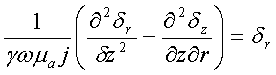
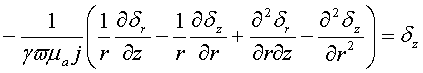 (3)
(3)
где ![]() - удельная проводимость.
- удельная проводимость.
Для
стационарного распределения плотности тока
![]() (4)
(4)
С
учётом (4) система дифференциальных уравнений преобразуется к виду:
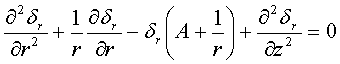
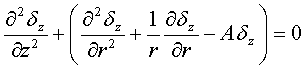 (5)
(5)
Здесь ![]() .
.
Система
дифференциальных уравнений (5) является математическим описанием распределения компонент
комплексного вектора плотности тока в сплошном цилиндрическом нагревателе.
Рассмотрим её при следующих граничных условиях:
![]()
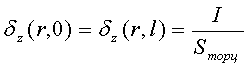
![]()
![]()
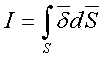 (6)
(6)
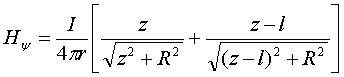
где ![]() - радиус проводника
- радиус проводника
![]() - его длина
- его длина
![]() - поверхность нагревателя.
- поверхность нагревателя.
Граничные
условия (6) записаны в силу физической реальности процесса. Последнее соотношение
(6) характеризует значение напряжённости магнитного поля на поверхности ![]() нагревателя [2].
Решим систему (5) с учётом граничных
условий (6) методом конечного косинус-преобразования Фурье [3], а также,
используя известные решения модифицированного уравнения Бесселя [4] в области
изображений. Осуществляя обратный переход в область оригиналов, получим:
нагревателя [2].
Решим систему (5) с учётом граничных
условий (6) методом конечного косинус-преобразования Фурье [3], а также,
используя известные решения модифицированного уравнения Бесселя [4] в области
изображений. Осуществляя обратный переход в область оригиналов, получим:
![]()
![]() (7)
(7)
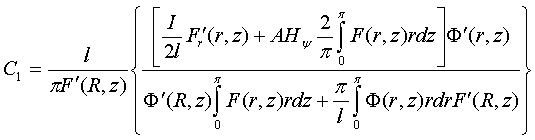
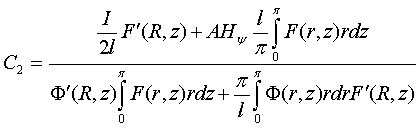 (8)
(8)
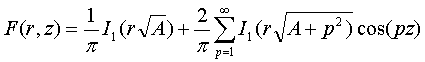
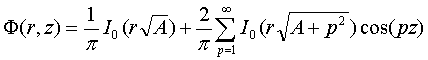 (9)
(9)
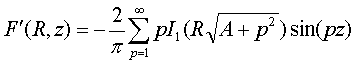
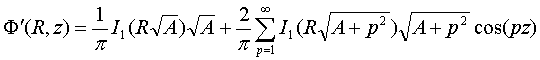
В
(9) ![]() - модифицированная
функция Бесселя I-го рода нулевого и первого
порядка соответственно.
- модифицированная
функция Бесселя I-го рода нулевого и первого
порядка соответственно.
Найденные
зависимости (7-9) характеризуют распределение плотности тока в сплошном
цилиндрическом нагревателе конечных размеров. Они устанавливают зависимость
плотности тока от геометрических и физических параметров нагревателя. Эти
зависимости пригодны для математического моделирования особенностей
распределения плотности тока при изменении определяющих параметров, а также для
вычисления интенсивности тепловыделений при описании поля температур и тепловых
потоков в рассматриваемом цилиндрическом нагревателе камеры высокого давления.
Литература
1.
С.Д. Купалян.
Теоретические основы электротехники. Т.2. Изд. ”Энергия”, М., 1970, с.105.
2.
А.Д. Нестеренко. Введение в теоретическую электротехнику,
Изд. ”Наукова думка”, Киев, 1969, с. 245.
3.
А.В. Лыков. Теория теплопроводности, Изд. ”Высшая школа”, М., 1969, с. 515.
4.
И.Н. Бронштейн, К.А. Семендяев. Справочник по математике, Изд. ”Наука”, М.,
1967, с. 463.