ИДЕНТИФИКАЦИЯ: МЕТОД ПОСЛЕДОВАТЕЛЬНОЙ РЕГРЕССИИ

¹Будылина Е.А., ²Гарькина И.А., ²Данилов А.М.

¹Московский государственный машиностроительный университет

²Пензенский государственный университет архитектуры и строительства

Рассмотрим метод последовательной регрессии в приложении к разработке авиационных тренажеров; а именно, к идентификации короткопериодической составляющей продольного движения [1]:

;

.

Для перехода от динамической задачи к статической используем метод конечных разностей. Имеем:

.

Коэффициенты должны определяться из условий минимума функционалов:

,

,

где - количество замеров вектора ; то есть из систем уравнений:

;	(1)
.	(2)

Системы (1), (2) аналогичны по своей структуре, поэтому метод идентификации рассмотрим на примере одной из них.

В матричной форме (1), (2) представятся в виде:

,	(3)
,	(4)

где 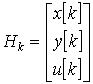, , 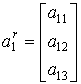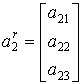( - равенство по определению).

Рассмотрим подробно последовательную регрессионную идентификацию на примере системы (3).

Введем

,

(5)

тогда (3) примет вид:

, .

(6)

Откуда из (6) и (3):

,

(7)

.

После несложных преобразований получим рекуррентную формулу для оценки :

.

(8)

Аналогично получили бы формулу для оценки :

.

(9)

Отметим, оценка может быть рекуррентно получена по предыдущей оценке и по измерениям , при условии, что матрица так же получена последовательно.

В соответствии с (5) имеем:

.

(10)

Предполагается известным начальное значение матрицы .

После несложных преобразований получим окончательное рекуррентное соотношение:

.

(11)

Начальная оценка может быть произвольной; нами принималось .

Метод прошел положительную апробацию.

Литература

1. Данилов А.М., Домке Э.Р., Гарькина И.А. Формализация оценки оператором характеристик объекта управления / Информационные системы и технологии, №2 (70), 2012. С.5-11.
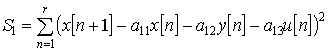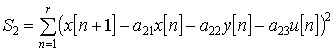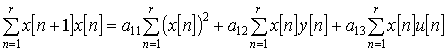
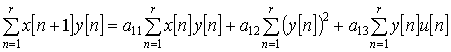
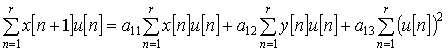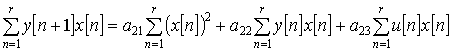
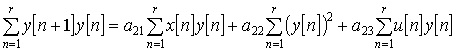
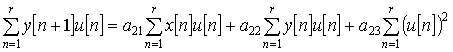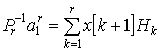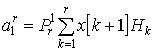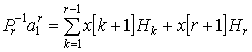