УДК: 51-74; 691:342; 691.327; 666.972.7

компьютерно-ИМИТАЦИОННОЕ моделированиЕ

структурообразования дисперсных систем

НАНОМОДИФИЦИРОВАННЫХ КОМПОЗИТОВ

А.Н. Бормотов

Россия, Пензенская государственная технологическая академия

aleks21618@yandex.ru

Композиционные материалы являются типичными дисперсными системами, полученными на основе маловязкой дисперсионной среды (вяжущее) и тонкомолотых дисперсных фаз. Эволюция дисперсно-наполненных материалов определяется взаимодействиями между структурообразующими элементами, в результате которых могут образовываться флокулы (кластеры), оказывающие значительное влияние, как на реологические свойства систем, так и на структуру и эксплуатационные свойства композиционных материалов. Поэтому установление закономерностей влияния рецептурно-технологических факторов на процесс структурообразования дисперсных систем позволяет целенаправленно изменять свойства композитов, что является одной из приоритетных научно-технических задач, решение которой имеет большое практическое значение.

Привлечение средств анализа требует записи решения системы дифференциальных уравнений в замкнутой форме, что позволяет исследовать эволюцию только двухчастичных моделей. Изучение процесса флокулообразования и установление статистических закономерностей, характерных для реальных дисперсных систем, возможно с применением методов численного анализа, так как число частиц в моделях таких систем должно быть достаточно велико (порядка 10²...10³).

Алгоритм численного анализа.

В основу алгоритма численного анализа положена система дифференциальных уравнений второго порядка в частных производных [1]:

, ,

(1)

где m_i - масса i-й частицы; - ее координаты; N – количество частиц наполнителя; k - коэффициент, определяемый диссипативными свойствами дисперсионной среды, v_i - скорость дисперсионной среды в точке r_i; U_i - потенциал в точке r_i (в общем случае зависящий от характеристик дисперсионной среды, а также от характеристик и взаимного расположения всех остальных частиц системы).

Полагая скорость частицы за новую переменную, записывая уравнение (1) в виде системы 6N обыкновенных дифференциальных уравнений и используя скалярный модуль силы парного взаимодействия, получим:

,

(2)

где - радиус-вектор системы частиц в 6N-мерном фазовом пространстве.

Устойчивый алгоритм интегрирования должен быть построен таким образом, чтобы в процессе расчета выполнялась оценка ошибок и полученная информация использовалась для корректировки шага по времени. Данное требование известно как требование адаптивного шага интегрирования.

Альтернативным алгоритмом контроля шага является алгоритм, основанный на методе вложенных форм. При использовании данного метода на каждом шаге интегрирования выполняется шесть вычислений правой части системы (2):

, .

(3)

Полученные значения используются с двумя наборами весовых коэффициентов , для нахождения фазы в точке t+h и для оценки ошибки интегрирования:

;	(4)
;	(5)
.	(6)

При использовании уравнений (3)...(6) предварительная корректировка шага интегрирования выполняется в соответствии с соотношением

,

(7)

где d - коэффициент, характеризующий точность решения.

Если новое значение шага h^* оказалось больше предыдущего h (точность на текущем шаге завышена), то полученное значение фазы принимается, и в качестве нового значения шага выбирается h^*. Если новое значение шага оказалось меньше (точность занижена по сравнению с требуемой), то значение отбрасывается, и расчет повторяется для меньшего шага h^*. В качестве нормы в уравнении (7) используется наибольший из модулей:

, .

(8)

Расчетная схема, представленная уравнениями (3)...(8), положена в основу программного обеспечения численного анализа.

Реализация алгоритма.

Решение системы (2) при начальных условиях возможно выполнить с использованием универсальных пакетов (Mathcad, MATLAB, Maple и др.), однако для подобного подхода характерна сравнительно невысокая вычислительная эффективность. Кроме того, процесс реализации расчетной схемы из уравнений (3)...(8) в рамках универсальных пакетов по затратам времени сопоставим с реализацией ее в автономном ПО.

Известны пакеты программного обеспечения, изначально ориентированные на представление систем частиц. Однако большая их часть предназначена не для проведения модельных экспериментов, а для расчета в реальном времени характеристик систем частиц, используемых в процессе визуализации специальных эффектов.

Для исследования эволюции дисперсных систем разработано не имеющее аналогов ПО. Программный продукт является автономным (не требует для работы других пакетов численного анализа) и реализован на стандартном языке ANSI C (ANSI X3.158-1989) для операционных систем Windows NT/2000, а также POSIX-совместимых вычислительных платформ.

Укрупненная блок-схема ПО приведена на рис. 1.

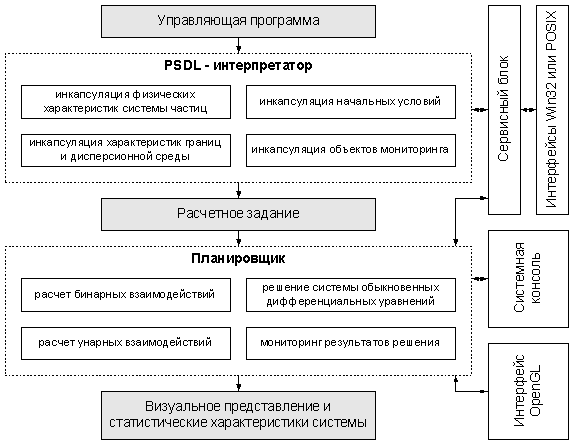
Рис. 1. Архитектура разработанного ПО численного анализа

Исполнение ПО начинается с синтаксического анализа командной строки, в которой передается имя управляющей программы.

Управляющая программа содержит текстовое описание моделируемой системы, в котором, в свою очередь, должны быть определены общие параметры системы (число сферических частиц, распределение их по размерам и плотности), начальные условия (пространственное распределение частиц), расположение и вид границ (плоскости, сферы), вид функций парного взаимодействия и взаимодействия с границами, численные значения коэффициентов, входящих в выражения для функций взаимодействия. Данная информация инкапсулируется в объекте, содержащем описание системы частиц.

Процесс моделирования начинается с создания объекта мониторинга, один из методов которого периодически вызывается в процессе решения. В данном объекте реализованы, в частности, процедуры статистического анализа и графического отображения результатов.

В процессе решения при каждом вызове функции вычисления правой части системы (2) выполняется ряд операций:

1. Нахождение значений сил парного взаимодействия:

, , ,

где - модуль силы парного взаимодействия; - вектор, соединяющий центры i-й и j-й частиц; , - радиусы i-й и j-й частиц, соответственно; N - число частиц.

2. Нахождение N значений силы тяжести

,

где m_i - масса i-й частицы.

3. Нахождение N значений силы вязкого трения

,

где h - вязкость среды; R_i, - радиус и скорость i-й частицы, соответственно; v - скорость дисперсионной среды.

4. Нахождение сил взаимодействия с границами.

Все граничные плоскости заданы уравнениями в нормальной форме:

, ,

где n_k - единичный вектор нормали k-й плоскости; - радиус-вектор текущей точки; p_k – расстояние от начала координат до k-й плоскости; K – число граничных плоскостей.

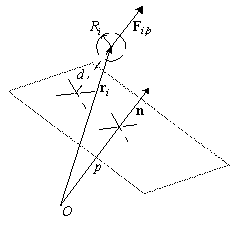
Вектор силы, действующей со стороны граничной плоскости, вычисляется на основании соотношения

,

где d_ik - расстояние от i-й частицы до k-й плоскости; R_i - радиус i-й частицы (рис. 2).

Размещая достаточное количество граничных плоскостей, можно учесть взаимодействие с границей сравнительно сложной формы. Однако для достижения максимальной вычислительной эффективности целесообразнее явно выразить силы взаимодействия с некоторыми другими видами граничных поверхностей.

Для определения граничной сферы достаточно указать ее центр и радиус (где , L - число граничных сфер).

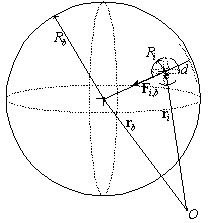
Вектор силы, действующей со стороны граничной сферы, вычисляется на основании соотношения

,

где d_il - расстояние от i-й частицы до l-й сферы (рис. 3).

Рис. 2. Схема взаимодействия частицы с граничной плоскостью

Рис. 3. Схема взаимодействия частицы с граничной сферой

Сумма сил тяжести, вязкого трения, парного взаимодействия и взаимодействия с граничными поверхностями, определяет силу, действующая на i-ю частицу и изменяющую ее положение:

.

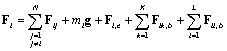Полученные значения сил используются для коррекции состояния дисперсной системы в соответствии с выбранной расчетной схемой.

Текущее значение состояния дисперсной системы используется для графического представления результатов расчета, а также для автоматической генерации программ на входном языке пакета 3D Studio MAX. После завершения расчета, полученные программы используются для создания растрового изображения моделируемой дисперсной системы.

Графические представления взаимного расположения частиц достаточно наглядны, однако не позволяют сделать выводы относительно значений характерного времени структурообразования и характерных перемещений частиц в процессе эволюции дисперсной системы. Оценить указанные параметры можно только на основе статистического анализа изменения положений частиц.

Для этого целесообразно использовать следующие показатели:

; ; ;

; ; ,

где - расстояния от поверхности i-й частицы (, N - число частиц) до поверхности четырех ближайших частиц (для i-й частицы усреднение проводится по числу ближайших); , - соответственно оценки среднего и среднего квадратичного отклонения расстояния от i-й частицы () до четырех ближайших к ней; - число частиц, расстояние до поверхности которых (от поверхности i-й частицы) не превышает заданного значения; , - соответственно оценки среднего и среднего квадратичного отклонения числа частиц, расстояние до которых от данной не превышает заданного значения; - число частиц, находящихся в k-й подобласти (, K - число подобластей) выпуклой оболочки всех N частиц; , - соответственно оценки среднего и среднего квадратичного отклонения числа частиц, находящихся в k-й подобласти () выпуклой оболочки всех частиц; K - число подобластей.

Для нахождения числа частиц производилось построение ограничивающего прямоугольного параллелепипеда, который затем разделялся на 27 равных подобластей.

Численный эксперимент.

Моделирование эволюции производилось для систем, объемная доля дисперсных частиц в которых варьировалась от 0,01 до 0,15, в результате которого были получены математические модели лиофобной, лиофильной систем и лиофильной системы при наличии сольватных слоев.

Полученной статистической информации достаточно для построения адекватных моделей и установления закономерностей влияния рецептурно-технологических факторов на процесс структурообразования дисперсных систем.

На основе приведенного подхода к компьютерно-имитационному моделированию композитов осуществлялась разработка композиционного материала на основе серного и эпоксидного вяжущих, модифицированного наноразмерным модификатором, приготовленным на основе астраленов (наночастиц) и ПАВ неионогенного типа.

Дальнейшее исследование и промышленная апробация разработанных композиционных материалов, показали высокую эффективность разработанного подхода при решении задач моделирования, анализа и синтеза наномодифицированных композиционных материалов.

Список литературы

1. Разработка и управление качеством строительных материалов с регулируемыми структурой и свойствами для защиты от радиации. / Бормотов А.Н. [и др.] // Тр. Междунар. конф. «Идентификация систем и задачи управления» SICPRO ’03. / Ин-т пробл. упр. – М., 2003. – С. 2437-2460.

Бормотов Алексей Николаевич – д.т.н., профессор кафедры автоматизации и управления ФГБОУ ВПО «Пензенская государственная технологическая академия», Россия.