Masich I.S.
Siberian State Aerospace University, Russia
Heuristic algorithms for searching
boundary points
in pseudo-Boolean optimization
problems
Unconstrained pseudo-Boolean optimization is an issue
that studied enough by now. Algorithms that have been designed and investigated
in the area of unconstrained pseudo-Boolean optimization are applied
successfully for solving various problems. Particularly, these are local
optimization methods and stochastic and regular algorithms based on local
search for special function classes [1]. Moreover, there are a number of
algorithms for optimization of functions given in explicit form [2]. Universal
optimization methods are also used successfully: genetic algorithms, simulated
annealing, tabu search.
If there are constraints on the binary variables, one
of ways to take into account it as is well known is construction and
optimization of an generalized penalty function. Shortcoming of this approach
is existence of a large number of local optima of the generalized function what
will be shown below. If an accessible region is a connected one then this issue
can be partly eliminated, for example, by using local search with a stronger
system of neighborhoods. Extension of search neighborhood reduces the number of
local optima which locate mainly not far one from another in this case.
If an accessible region is unconnected then using
penalty functions and unconstrained optimization methods get complicated
because the accessible region is usually too small with respect to optimization
space. That makes difficult searching feasible solution.
In this work heuristic procedures of boundary point
search are considered for a constrained pseudo-Boolean optimization problem.
Experimental investigation of the algorithms are described, recommendations for
their applying are given.
Consider the problem of the following form
![]() , (1)
, (1)
where ![]() is a monotonically increasing
from
is a monotonically increasing
from ![]() pseudo-Boolean function,
pseudo-Boolean function,
![]() is a
certain subregion of the binary variable space; it is determined by a given constraint
system, for example:
is a
certain subregion of the binary variable space; it is determined by a given constraint
system, for example:
![]() . (2)
. (2)
In the general case a set of feasible solutions S is a unconnected set.
For any heuristic of boundery point search we will
consider a pair of algorithms – primary and dual. A primary algorithm starts
search from the feasible area and moves in a path of increasing of the
objective function until it finds a limiting point of feasible area. Otherwise,
a dual algorithm keeps search in the unfeasible area in a path of decreasing of the
objective function until it finds some available solution.
Total scheme of
primary search algorithm
1. Put ![]() ,
, ![]() .
.
2.
In accordance with a rule we choose ![]() . If there are no such point then go to 3; else
. If there are no such point then go to 3; else ![]() and repeat the step.
and repeat the step.
3. ![]() .
.
Total scheme of
dual search algorithm
1. Put ![]() ,
, ![]() .
.
2.
In accordance with a rule we choose ![]() . If
. If ![]() then go to 3; else
then go to 3; else ![]() and repeat the step.
and repeat the step.
3. ![]() .
.
Here ![]() is the set of all points k-neighboring to X (level k of point X).
is the set of all points k-neighboring to X (level k of point X).
From these schemes we can see that a primary algorithm finds a limiting point of the feasible area,
but a dual algorithm finds a boundary point which may be not a limiting one. So a primary algorithm finds
a better solution then dual in most cases for problems with a connected set of
feasible solutions. If we will use a primary algorithm for a problem with a
unconnected feasible area then solution received in result may be far from the
optimal because feasible and unfeasible solutions will rotate in a path of
increasing of the objective function. For these cases a dual algorithm is more
usefull, because this rotation do not play any role for it. For improving the
solution that given by the dual algorithm, it is recommends to apply the
corresponding primary algorithm. Such improving is very significant in
practice.
Boundary point search algorithms considered below
differs by only a rule of choise of a next point in step 2 of the total
schemes.
Search rules
Rule 1. Random search of boundary points (RSB)
A point ![]() is chosen by random way. Each point in the next step can
be chosen with equal probabilities. For real-world problems these probabilities
can be not equal but they are calculated in the basis of problem specific
before search starts.
is chosen by random way. Each point in the next step can
be chosen with equal probabilities. For real-world problems these probabilities
can be not equal but they are calculated in the basis of problem specific
before search starts.
Rule 2. Greedy algorithm
A point
![]() is chosen acordance
with the condition
is chosen acordance
with the condition
![]() ,
,
where ![]() for a primary algorithm and
for a primary algorithm and ![]() for a dual one.
for a dual one.
The function ![]() is chosen from problem
specific, for example:
is chosen from problem
specific, for example:
the objective function ![]() ,
,
specific value ![]() (for only constraint) and so on.
(for only constraint) and so on.
Rule 3. Adaptive random search
of boundary points (ARSB)
A point
![]() is chosen by random
way in accordance with a probability vector
is chosen by random
way in accordance with a probability vector
![]() ,
,
where J
is the
number of points from which choice is made.
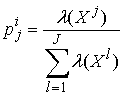 ,
, ![]() ,
,
where ![]() for a
primary algorithm and
for a
primary algorithm and ![]() for a dual one.
for a dual one.
ARSB is a addition to the greddy algorithm.
Rule 4. Modificated random search of boundary points (MRSB)
A point
![]() is chosen
accordance with the condition
is chosen
accordance with the condition
![]() ,
,
where ![]() are points chosen accordance
with the rule 1,
are points chosen accordance
with the rule 1, ![]() ; R is a algorithm parameter.
; R is a algorithm parameter.
References
1.
Antamoshkin A.N. Regular
optimization of pseudo-Boolean functions. – Krasnoyarsk: Krasnoyarsk university
publ., 1989, 284 p.
2. Boros E., Hammer P.L. Pseudo-Boolean Optimization.
Discrete Applied Mathematics 123(1-3): 155-225 (2002).