Система изучения темы «Интеграл» высшей математики на экономических специальностях вузов

В.В.Подгорная

г. Минск, Учреждение образования Федерации профсоюзов Беларуси «Международный институт трудовых и социальных отношений»

Мы будем рассматривать формирование математических умений у будущих экономистов, при этом напомним, что перед математикой, как перед одной из основных составляющих профессионального образования поставлен целый комплекс задач. Большой диапазон различных задач, стоящих перед курсом высшей математики в ВУЗе требует привлечения широкого арсенала дидактических средств.

Сегодня методическая система бучения математике просто вынуждена интенсифицировать свои возможности. В настоящее время у нас накоплен достаточно обширный опыт по многоуровневой системе изучения отдельных тем высшей математики. Предлагаемая система изучения материала по высшей математике– это организация обучения, которая создает оптимальные условия для развития индивидуальных способностей обучаемых. При таком подходе студенты самостоятельно определяют уровень овладения учебным материалом с учетом проведенных тестовых контрольных работ, предложенных преподавателем.

Условно всех обучающихся можно разделить на две группы: первый уровень и второй уровень, конечно уровней может быть и больше, все зависит от степени подготовки студентов.

Первоначально студентам предлагаются тестовые задания с помощью, которых они определяют уровень своих знаний и соответственно уровень обучения, после этого они работают с демонстрационными примерами разного уровня сложности.

1. Найти интеграл .

Воспользуемся линейностью неопределенного интеграла, неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от слагаемых функций:

.

Вынесем постоянные множители за знаки интегралов:

.

Воспользуемся таблицей неопределенных интегралов:

.

Заметим, что произвольные постоянные, получающиеся при интегрировании каждого слагаемого, здесь объединены в одну произвольную постоянную C.

2. Найти интеграл .

Разделим почленно числитель на знаменатель и воспользуемся свойством линейности и таблицей неопределенных интегралов:

.

3. Найти интеграл .

Прибавим и вычтем из числителя 1, а затем разделим почленно числитель на знаменатель:

.

4. Найти интеграл .

Данный интеграл не является табличным, т. к. аргумент функции (2х) не совпадает с переменной, стоящей под знаком дифференциала (x). Следовательно, подстановка приведет данный интеграл к табличному. Не следует забывать, что, вводя новую переменную t необходимо ввести и ее дифференциал dt и перейти в подынтегральном выражении к новой переменной и ее дифференциалу.

.

Теперь необходимо вернуться к исходной переменной:

.

Этот же результат можно получить, поднеся 2x под знак дифференциала, т. е. заметив, что , а, следовательно, :

.

5. Найти интеграл .

Так как функция x при дифференцировании «упрощается» , а при интегрировании «усложняется» , а функция e^x остается неизменной, то :

.

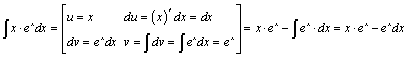После изучения демонстрационных примеров студенты выполняют разноуровневые самостоятельные обучающие работы.

1. Найти интеграл ;

2. Найти интеграл ;

3. Найти интеграл ;

4. Найти интеграл ;

5. Найти интеграл ;

6. Найти интеграл ;

7. Найти интеграл ;

8. Найти интеграл ;

9. Найти интеграл ;

10. Найти интеграл .

Использование такого подхода в обучении решению задач по высшей математике способствует развитию следующих способностей:

1. правильно определять свои запросы и возможности

2. прогнозировать пути развития ситуации

3. правильно выбирать необходимую для выполнения задания информацию

4. развивает аналитические способности

Литература

1. М.С. Красс, В.П. Чупрынов, «Математика для экономистов», Москва – Санкт – Петербург, 2010 г.;

2. М.С. Красс, «Математика для экономических специальностей», Дело, 2003 г.