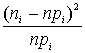Педагогические науки/5. Современные методики преподавания

к.ф.-м. н. Михин М.Н., Полозюк А.Г.

Московский государственный университет приборостроения и информатики

Использование коэффициентов асимметрии и эксцесса при выборе гипотезы о виде закона распределения генеральной совокупности

Во многих задачах необходимо, используя результаты наблюдений, выбрать закон распределения генеральной совокупности. Как правило, для этого используют гистограмму или полигон частот (относительных частот). В тоже время можно использовать только числовые характеристики (математическое ожидание, дисперсия, коэффициент асимметрии и коэффициент эксцесса). Закон распределения вполне определяется коэффициентами асимметрии и эксцесса

, ,

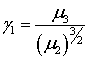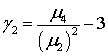где — выборочные центральные моменты второго, третьего и четвертого порядка соответственно.

Напомним, что выборочные центральные моменты определяются по формуле

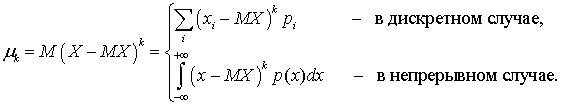
Можно заметить, что в тех случаях, когда коэффициенты асимметрии и эксцесса зависят от параметров распределения (закон Пуассона , , хи-квадрат распределение , и др.) коэффициент эксцесса выражается через квадрат коэффициента асимметрии.

На рисунке 1 показано соотношение между коэффициентами асимметрии и эксцесса для некоторых распределений

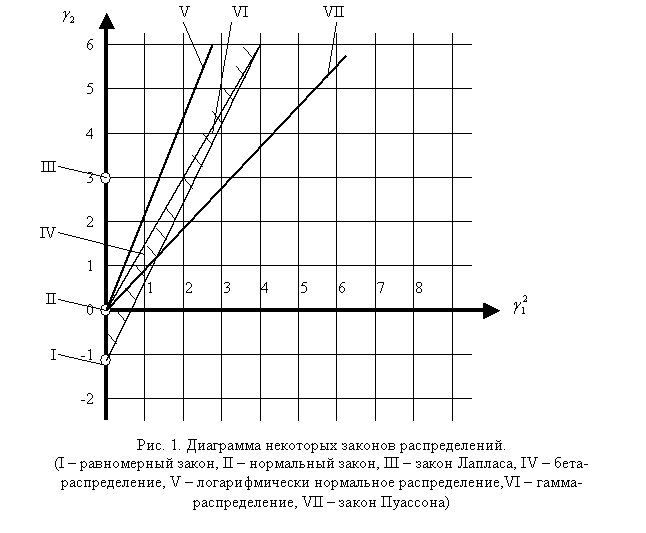
Если точка оказывается вблизи от точки, прямой или области, соответствующих одному из распределений, то его следует выдвинуть в качестве гипотезы распределения исследуемой случайной величины. Проверка гипотезы о виде закона распределения и оценка параметров распределения осуществляется на основе известных методов.

Рассмотрим пример. Для случайной выборки

Xi	0	1	2	3	4	5	6	7
ni	3	8	12	11	9	4	2	1

определить закон распределения и проверить гипотезу о виде закона распределения приняв уровень значимости 0,05.

Вычислив квадрат коэффициента асимметрии и коэффициент эксцесса

,

выдвигаем гипотезу «генеральная совокупность распределена по закону Пуассона».

На основании полученных данных вычисляем оценку параметра распределения Пуассона

.

Для нахождения расчетного значения критерия воспользуемся вспомогательной таблицей

0	3	0,058	0,002
1	8	0,166	0,011
2	12	0,236	0,004
3	11	0,223	0,002
4	9	0,158	0,148
5	3	0,090	0,499
6	2	0,043	0,008
7	2	0,017	1,495
		1	2,168

где 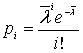— теоретические вероятности.

Таким образом получаем

.

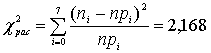Критическое значение найдем, используя функцию ХИ2ОБР из Excel.

.

Так как , то рассматриваемая гипотеза о распределении Пуассона принимается.

Таким образом, при проведении занятий о применении критериев согласия задание можно формулировать следующим образом «Используя коэффициенты асимметрии и эксцесса выдвинуть и проверить гипотезу о виде закона распределения генеральной совокупности».

Л

итература

1. Hines W.W., Montgomery D.C., Goldsman D.M., and Borror C.M. Probability and Statistics in Engineering, 4th Edition, Wiley, New York, 2003.

2. Seely J.A. Probability and Statistics for Engineering and Science, 6th Sol. Mn Edition, Brooks Cole, Stamford, 2003.

3. Михин М.Н., Пяткин В.В. О проблеме выбора закона распределения генеральной совокупности. Сборник трудов по материалам международной научно-практической конференции «Современные проблемы и пути их решения в науке, транспорте, производстве и образовании 2010». Т.8. Физика и математика. — Одесса: Черноморье, 2010. C.24-26.